
Unknotting problem
Encyclopedia
In mathematics
, the unknotting problem is the problem of algorithmically recognizing the unknot
, given some representation of a knot, e.g., a knot diagram. There are several types of unknotting algorithms. A major unresolved challenge is to determine if the problem admits a polynomial time algorithm, that is, whether the problem lies in the complexity class P
.
in larger complexity classes, which contain the class P. By using normal surface
s to describe the Seifert surface
s of a given knot, Hass, Lagarias and Pippenger showed that the unknotting problem is in the complexity class NP
, and it is also known to belong to the intersection AM coAM. Ian Agol has claimed a proof that unknotting is in NP
coAM. Ian Agol has claimed a proof that unknotting is in NP
 co-NP. Since AM is a generalization of NP
co-NP. Since AM is a generalization of NP
, the above mentioned
complexity classes are related by the following sequence of set inclusions:
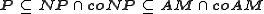 .
.
The unknotting problem has the same computational complexity as testing whether an embedding of an undirected graph in Euclidean space
is linkless
.
Understanding the complexity of these algorithms is an active field of study.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the unknotting problem is the problem of algorithmically recognizing the unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
, given some representation of a knot, e.g., a knot diagram. There are several types of unknotting algorithms. A major unresolved challenge is to determine if the problem admits a polynomial time algorithm, that is, whether the problem lies in the complexity class P
P (complexity)
In computational complexity theory, P, also known as PTIME or DTIME, is one of the most fundamental complexity classes. It contains all decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time.Cobham's thesis holds...
.
Computational complexity
First steps toward determining the computational complexity were undertaken in proving that the problem isin larger complexity classes, which contain the class P. By using normal surface
Normal surface
In mathematics, a normal surface is a surface inside a triangulated 3-manifold that intersects each tetrahedron so that each component of intersection is a triangle or a quad . A triangle cuts off a vertex of the tetrahedron while a quad separates pairs of vertices...
s to describe the Seifert surface
Seifert surface
In mathematics, a Seifert surface is a surface whose boundary is a given knot or link.Such surfaces can be used to study the properties of the associated knot or link. For example, many knot invariants are most easily calculated using a Seifert surface...
s of a given knot, Hass, Lagarias and Pippenger showed that the unknotting problem is in the complexity class NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
, and it is also known to belong to the intersection AM
 coAM. Ian Agol has claimed a proof that unknotting is in NP
coAM. Ian Agol has claimed a proof that unknotting is in NPNP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
 co-NP. Since AM is a generalization of NP
co-NP. Since AM is a generalization of NPNP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
, the above mentioned
complexity classes are related by the following sequence of set inclusions:
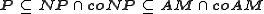 .
.The unknotting problem has the same computational complexity as testing whether an embedding of an undirected graph in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is linkless
Linkless embedding
In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into Euclidean space in such a way that no two cycles of the graph have nonzero linking number. A flat embedding is an embedding with the property that every cycle is the...
.
Unknotting algorithms
Some known algorithms solving the unknotting problem include:- HakenWolfgang HakenWolfgang Haken is a mathematician who specializes in topology, in particular 3-manifolds.In 1976 together with colleague Kenneth Appel at the University of Illinois at Urbana-Champaign, Haken solved one of the most famous problems in mathematics, the four-color theorem...
's algorithm - uses the theory of normal surfaceNormal surfaceIn mathematics, a normal surface is a surface inside a triangulated 3-manifold that intersects each tetrahedron so that each component of intersection is a triangle or a quad . A triangle cuts off a vertex of the tetrahedron while a quad separates pairs of vertices...
s to check for a normal disc bound by the knot - An upper bound (exponential in crossing number) exists on the number of Reidemeister moveReidemeister moveIn the mathematical area of knot theory, a Reidemeister move refers to one of three local moves on a link diagram. In 1926, Kurt Reidemeister and independently, in 1927, J.W. Alexander and G.B...
s needed to change an unknot diagram to the standard unknot diagram, from the work of Hass and Lagarias on Reidemeister moves. This lends itself for a (very slow) brute-force search algorithm. - BirmanJoan BirmanJoan Sylvia Lyttle Birman is an American mathematician, specializing in braid theory and knot theory. Her book Braids, Links, and Mapping Class Groups has become a standard introduction, with many of today's researchers having learned the subject through it...
-Hirsch algorithm - uses braid foliations - Residual finiteness of the knot groupKnot groupIn mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,\pi_1....
(which follows from geometrizationGeometrization conjectureThurston's geometrization conjecture states that compact 3-manifolds can be decomposed canonically into submanifolds that have geometric structures. The geometrization conjecture is an analogue for 3-manifolds of the uniformization theorem for surfaces...
of Haken manifoldHaken manifoldIn mathematics, a Haken manifold is a compact, P²-irreducible 3-manifold that is sufficiently large, meaning that it contains a properly embedded two-sided incompressible surface...
s) gives a rather inefficient algorithm: check if the group has a representation into a symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
with non-cyclic image while simultaneously attempting to produce a subdivision of the triangulated complement that is equivalent to a subdivision of the triangulated solid torusSolid torusIn mathematics, a solid torus is a topological space homeomorphic to S^1 \times D^2, i.e. the cartesian product of the circle with a two dimensional disc endowed with the product topology. The solid torus is a connected, compact, orientable 3-dimensional manifold with boundary...
. - Knot Floer homology of the knot detects the genus of the knot, which is 0 if and only if the knot is an unknot. A combinatorial version of knot Floer homology allows a straightforward computation.
- Khovanov homologyKhovanov homologyIn mathematics, Khovanov homology is an invariant of oriented knots and links that arises as the homology of a chain complex. It may be regarded as a categorification of the Jones polynomial....
detects the unknot according to a result of KronheimerPeter B. KronheimerPeter Benedict Kronheimer is a British mathematician, known for his work on gauge theory and its applications to 3- and 4-dimensional topology. He is presently William Casper Graustein Professor of Mathematics at Harvard University....
and MrowkaTomasz MrowkaTomasz Mrowka is a Polish American mathematician. He has been the Singer Professor of Mathematics at Massachusetts Institute of Technology since 2010. A graduate of MIT, he received the Ph.D. from University of California, Berkeley in 1988 under the direction of Clifford Taubes and Robion Kirby...
. Khovanov homology can be computed reasonably efficiently, for instance using a program by Dror Bar-NatanDror Bar-NatanDror Bar-Natan is a mathematics professor at the University of Toronto, Canada. His main research interests include knot theory, finite type invariants, and Khovanov homology.-Education:...
.
Understanding the complexity of these algorithms is an active field of study.
External links
- Complexity Zoo provides information about complexity classes and their inclusion relations.

