
Knot group
Encyclopedia
In mathematics
, a knot
is an embedding
of a circle
into 3-dimensional Euclidean space
. The knot group of a knot K is defined as the fundamental group
of the knot complement
of K in R3,
Other conventions consider knots to be embedded in the 3-sphere, in which case the knot group is the fundamental group of its complement in S3
and can be used to distinguish between inequivalent knots. This is because an equivalence between two knots is a self homeomorphism of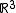 isotopic to the identity sending the first knot onto the second. Clearly the homeomorphism restricts onto a homeomorphism of the complement of the knot therefore inducing an isomorphism in the fundamental group of the knot complement. However, two knots can have isomorphic knot groups without necessarily being equivalent (see below for an example).
isotopic to the identity sending the first knot onto the second. Clearly the homeomorphism restricts onto a homeomorphism of the complement of the knot therefore inducing an isomorphism in the fundamental group of the knot complement. However, two knots can have isomorphic knot groups without necessarily being equivalent (see below for an example).
The abelianization of a knot group is always isomorphic to the infinite cyclic group
Z; this follows because the abelianization agrees with the first homology group, which can be easily computed.
The knot group (or fundamental group of an oriented link in general) can be computed in the Wirtinger presentation by a relatively simple algorithm.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
is an embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
into 3-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. The knot group of a knot K is defined as the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the knot complement
Knot complement
In mathematics, the knot complement of a tame knot K is the complement of the interior of the embedding of a solid torus into the 3-sphere. To make this precise, suppose that K is a knot in a three-manifold M. Let N be a thickened neighborhood of K; so N is a solid torus...
of K in R3,

Other conventions consider knots to be embedded in the 3-sphere, in which case the knot group is the fundamental group of its complement in S3
Properties
Two equivalent knots have isomorphic knot groups, so the knot group is a knot invariantKnot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
and can be used to distinguish between inequivalent knots. This is because an equivalence between two knots is a self homeomorphism of
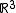 isotopic to the identity sending the first knot onto the second. Clearly the homeomorphism restricts onto a homeomorphism of the complement of the knot therefore inducing an isomorphism in the fundamental group of the knot complement. However, two knots can have isomorphic knot groups without necessarily being equivalent (see below for an example).
isotopic to the identity sending the first knot onto the second. Clearly the homeomorphism restricts onto a homeomorphism of the complement of the knot therefore inducing an isomorphism in the fundamental group of the knot complement. However, two knots can have isomorphic knot groups without necessarily being equivalent (see below for an example).The abelianization of a knot group is always isomorphic to the infinite cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
Z; this follows because the abelianization agrees with the first homology group, which can be easily computed.
The knot group (or fundamental group of an oriented link in general) can be computed in the Wirtinger presentation by a relatively simple algorithm.
Examples
- The unknotUnknotThe unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
has knot group isomorphic to Z. - The trefoil knotTrefoil knotIn topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
has knot group isomorphic to the braid groupBraid groupIn mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
B3. This group has the presentationPresentation of a groupIn mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
-
 or
or 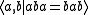 .
.
- A (p,q)-torus knotTorus knotIn knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q...
has knot group with presentation
- A (p,q)-torus knot
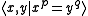 .
.
- The figure eight knotFigure-eight knot (mathematics)In knot theory, a figure-eight knot is the unique knot with a crossing number of four. This is the smallest possible crossing number except for the unknot and trefoil knot...
has knot group with presentation
- The figure eight knot
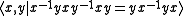
- The square knotSquare knot (mathematics)In knot theory, the square knot is a composite knot obtained by taking the connected sum of two trefoil knots. It is closely related to the granny knot, which is also a connected sum of two trefoils...
and the granny knotGranny knot (mathematics)In knot theory, the granny knot is a composite knot obtained by taking the connected sum of two identical trefoil knots. It is closely related to the square knot, which can also be described as a connected sum of two trefoils...
have isomorphic knot groups, yet these two knots are inequivalent.
- The square knot

