Torus knot - AbsoluteAstronomy.com

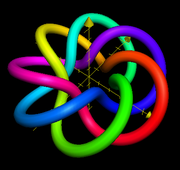
Knot theory

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...

, a torus knot is a special kind of knot

Knot (mathematics)

In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...

that lies on the surface of an unknotted torus

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

in R³. Similarly, a torus link is a link

Link (knot theory)

In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...

which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime

Coprime

In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...

integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s p and q. A torus link arises if p and q are not coprime. A torus knot is trivial

Unknot

The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...

if and only if

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

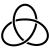
either p or q is equal to 1 or −1. The simplest nontrivial example is the (2,3)-torus knot, also known as the trefoil knot

Trefoil knot

In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...

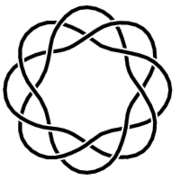
Geometrical representation

A torus knot can be rendered geometrically in multiple ways which are topologically equivalent (see Properties below) but geometrically distinct. The convention used in this article and its figures is the following.

The (p,q)-torus knot winds q times around a circle in the interior of the torus,
and p times around its axis of rotational symmetry. If p and q are not relatively prime, then we have a torus link with more than one component.

The direction in which the strands of the knot wrap around the torus is also subject to differing conventions. The most common is to have the strands form a right-handed screw for p q > 0 .

The (p,q)-torus knot can be given by the parametrization

Parametrization

Parametrization is the process of deciding and defining the parameters necessary for a complete or relevant specification of a model or geometric object....

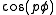
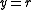
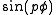
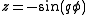
where

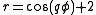and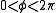

. This lies on the surface of the torus given by

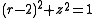(in cylindrical coordinates).

Other parametrizations are also possible, because knots are defined up to continuous deformation. The illustrations for the (2,3)- and (3,8)-torus knots can be obtained by taking

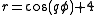, and in the case of the (2,3)-torus knot by furthermore subtracting respectively

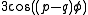and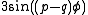

from the above parametrizations of x and y. The latter generalizes smoothly to any coprime p,q satisfying

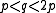Properties

A torus knot is trivial

Unknot

iff

If and only if

In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....

either p or q is equal to 1 or −1 .

Each torus knot is prime

Prime knot

In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...

and chiral

Chirality (mathematics)

In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...

.

The (p,q) torus knot is equivalent to the (q,p) torus knot . This can be proved by moving the strands on the surface of the torus, which is nicely illustrated here. The (p,−q) torus knot is the obverse (mirror image) of the (p,q) torus knot . The (−p,−q) torus knot is equivalent to the (p,q) torus knot except for the reversed orientation.
Any (p,q)-torus knot can be made from a closed braid

Braid theory

In topology, a branch of mathematics, braid theory is an abstract geometric theory studying the everyday braid concept, and some generalizations. The idea is that braids can be organized into groups, in which the group operation is 'do the first braid on a set of strings, and then follow it with a...

with p strands. The appropriate braid word is

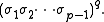
(Please note that this formula assumes the common convention that braid generators are right twists , which is not followed by the Wikipedia page on braids.)

The crossing number

Crossing number (knot theory)

In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....

of a (p,q) torus knot with p,q > 0 is given by

c = min((p−1)q, (q−1)p).

The genus of a torus knot with p,q > 0 is

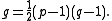
The Alexander polynomial

Alexander polynomial

In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...

of a torus knot is

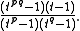
The Jones polynomial of a (right-handed) torus knot is given by

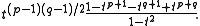
The complement of a torus knot in the 3-sphere

3-sphere

In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...

is a Seifert-fibered manifold

Seifert fiber space

A Seifert fiber space is a 3-manifold together with a "nice" decomposition as a disjoint union of circles. In other words it is a S^1-bundle over a 2-dimensional orbifold...

, fibred over the disc with two singular fibres.

Let Y be the p-fold dunce cap

Dunce hat (topology)

For the item of clothing designed to be humiliating, now rarely used, see dunce cap.In topology, the dunce hat is a compact topological space formed by taking a solid triangle and gluing all three sides together, with the orientation of one side reversed...

with a disk removed from the interior, Z be the q-fold dunce cap with a disk removed its interior, and X be the quotient space obtained by identifying Y and Z along their boundary circle. The knot complement of the (p, q)-torus knot deformation retract

Deformation retract

In topology, a branch of mathematics, a retraction , as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.- Retract :...

s to the space X. Therefore, the knot group

Knot group

In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,\pi_1....

of a torus knot has the presentation

Presentation of a group

In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...

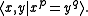
Torus knots are the only knots whose knot groups have nontrivial center (which is infinite cyclic, generated by the element

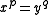in the presentation above).

Connection to complex hypersurfaces

The (p,q)−torus knots arise when considering the link of an isolated complex hypersurface singularity. One intersects the complex hypersurface with a hypersphere, centred at the isolated singular point, and with sufficiently small radius so that it does not enclose, nor encounter, any other singular points. The intersection gives a submanifold of the hypersphere.

Let p and q be coprime integers, greater than or equal to two. Consider the holomorphic function

Holomorphic function

In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...

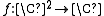given by

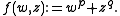Let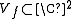

be the set of

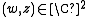such that

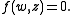Given a real number

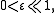we define the real three-sphere

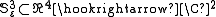as given by

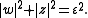Tne function

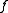has an isolated critical point

Critical point

Critical point may refer to:*Critical point *Critical point *Critical point *Construction point of a ski jumping hill-See also:*Brillouin zone*Percolation thresholds...

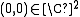since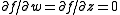

if and only if

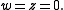Thus, we consider the structure of

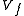close to

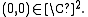In order to do this, we consider the intersection

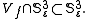This intersection is the so-called link of the singularity

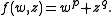The link of

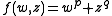, where p and q are coprime, and both greater than or equal to two, is exactly the (p,q)−torus knot.