Prime knot
Encyclopedia
In knot theory
, a prime knot is a knot
that is, in a certain sense, indecomposable. Specifically, it is a non-trivial
knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a given knot is prime or not.
A nice family of examples of prime knots are the torus knot
s. These are formed by wrapping a circle around a torus
p times in one direction and q times in the other, where p and q are coprime
integers.
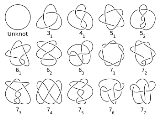
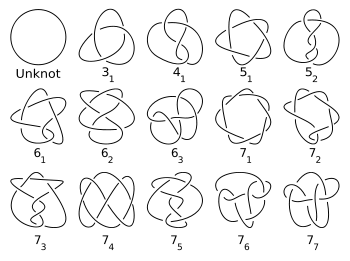
The simplest prime knot is the trefoil
with three crossings. The trefoil is actually a (2, 3)-torus knot. The figure-eight knot
, with four crossings, is the simplest non-torus knot. For any positive integer
n, there are a finite number of prime knots with n crossings
. The first few values are given in the following table.
Note that enantiomorphs
are counted only once in this table and the following chart (i.e. a knot and its mirror image
are considered equivalent).
of prime knots.
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, a prime knot is a knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
that is, in a certain sense, indecomposable. Specifically, it is a non-trivial
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a given knot is prime or not.
A nice family of examples of prime knots are the torus knot
Torus knot
In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q...
s. These are formed by wrapping a circle around a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
p times in one direction and q times in the other, where p and q are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
integers.
The simplest prime knot is the trefoil
Trefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
with three crossings. The trefoil is actually a (2, 3)-torus knot. The figure-eight knot
Figure-eight knot (mathematics)
In knot theory, a figure-eight knot is the unique knot with a crossing number of four. This is the smallest possible crossing number except for the unknot and trefoil knot...
, with four crossings, is the simplest non-torus knot. For any positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n, there are a finite number of prime knots with n crossings
Crossing number (knot theory)
In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
. The first few values are given in the following table.
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Number of prime knots with n crossings |
0 | 0 | 1 | 1 | 2 | 3 | 7 | 21 | 49 | 165 | 552 | 2176 | 9988 | 46972 | 253293 | 1388705 |
Note that enantiomorphs
Chirality (mathematics)
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. For example, a right shoe is different from a left shoe, and clockwise is different from counterclockwise.A chiral object...
are counted only once in this table and the following chart (i.e. a knot and its mirror image
Mirror image
A mirror image is a reflected duplication of an object that appears identical but reversed. As an optical effect it results from reflection off of substances such as a mirror or water. It is also a concept in geometry and can be used as a conceptualization process for 3-D structures...
are considered equivalent).

Schubert's theorem
A theorem due to Horst Schubert states that every knot can be uniquely expressed as a connected sumConnected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
of prime knots.

