
Granny knot (mathematics)
Encyclopedia
In knot theory
, the granny knot is a composite knot obtained by taking the connected sum of two identical trefoil knot
s. It is closely related to the square knot
, which can also be described as a connected sum of two trefoils. Because the trefoil knot is the simplest nontrivial knot, the granny knot and the square knot are the simplest of all composite knots.
The granny knot is the mathematical version of the common granny knot
.
It is important that the original trefoil knots be identical to each another. If mirror-image trefoil knots are used instead, the result is a square knot.
of a granny knot is six, which is the smallest possible crossing number for a composite knot. Unlike the square knot, the granny knot is not a ribbon knot
or a slice knot.
The Alexander polynomial
of the granny knot is
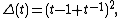
which is simply the square of the Alexander polynomial of a trefoil knot. Similarly, the Conway polynomial
of a granny knot is
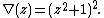
These two polynomials are the same as those for the square knot. However, the Jones polynomial for the (right-handed) granny knot is
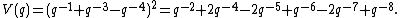
This is the square of the Jones polynomial for the right-handed trefoil knot, and is different from the Jones polynomial for a square knot.
The knot group
of the granny knot is given by the presentation
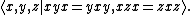
This is isomorphic
to the knot group of the square knot, and is the simplest example of two different knots with isomorphic knot groups.
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the granny knot is a composite knot obtained by taking the connected sum of two identical trefoil knot
Trefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
s. It is closely related to the square knot
Square knot (mathematics)
In knot theory, the square knot is a composite knot obtained by taking the connected sum of two trefoil knots. It is closely related to the granny knot, which is also a connected sum of two trefoils...
, which can also be described as a connected sum of two trefoils. Because the trefoil knot is the simplest nontrivial knot, the granny knot and the square knot are the simplest of all composite knots.
The granny knot is the mathematical version of the common granny knot
Granny knot
The granny knot is a binding knot, used to secure a rope or line around an object. It is considered inferior to the reef knot, which it superficially resembles. Neither of these knots should be used as a bend for attaching two ropes together....
.
Construction
The granny knot can be constructed from two identical trefoil knots, which must either be both left-handed or both right-handed. Each of the two knots is cut, and then the loose ends are joined together pairwise. The resulting connected sum is the granny knot.It is important that the original trefoil knots be identical to each another. If mirror-image trefoil knots are used instead, the result is a square knot.
Properties
The crossing numberCrossing number (knot theory)
In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
of a granny knot is six, which is the smallest possible crossing number for a composite knot. Unlike the square knot, the granny knot is not a ribbon knot
Ribbon knot
In the mathematical area of knot theory, a ribbon knot is a knot that bounds a self-intersecting disc with only ribbon singularities. This type of singularity is a self-intersection along an arc; the preimage of this arc consists of two arcs in the disc, one properly embedded in the disc and the...
or a slice knot.
The Alexander polynomial
Alexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
of the granny knot is
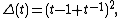
which is simply the square of the Alexander polynomial of a trefoil knot. Similarly, the Conway polynomial
Conway polynomial
In mathematics, Conway polynomial can refer to:* the Alexander–Conway polynomial in knot theory* the Conway polynomial...
of a granny knot is
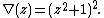
These two polynomials are the same as those for the square knot. However, the Jones polynomial for the (right-handed) granny knot is
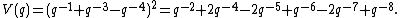
This is the square of the Jones polynomial for the right-handed trefoil knot, and is different from the Jones polynomial for a square knot.
The knot group
Knot group
In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,\pi_1....
of the granny knot is given by the presentation
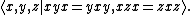
This is isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to the knot group of the square knot, and is the simplest example of two different knots with isomorphic knot groups.

