Ribbon knot
Encyclopedia
In the mathematical
area of knot theory
, a ribbon knot is a knot
that bounds a self-intersecting disc with only ribbon singularities. This type of singularity is a self-intersection along an arc; the preimage of this arc consists of two arcs in the disc, one properly embedded in the disc and the other completely in the interior of the disc.
Every ribbon knot is known to be slice. A famous question of Ralph Fox
asks if the converse is true: is every slice knot ribbon?
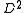in 
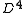with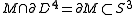 
. Consider the function 
given by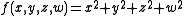 
. By a small isotopy of M one can ensure that f restricts to a Morse function on M. One says 
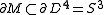is a ribbon knot if 
has no local maxima.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
area of knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, a ribbon knot is a knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
that bounds a self-intersecting disc with only ribbon singularities. This type of singularity is a self-intersection along an arc; the preimage of this arc consists of two arcs in the disc, one properly embedded in the disc and the other completely in the interior of the disc.
Every ribbon knot is known to be slice. A famous question of Ralph Fox
Ralph Fox
Ralph Hartzler Fox was an American mathematician. As a professor at Princeton University, he taught and advised many of the contributors to the Golden Age of differential topology, and he played an important role in the modernization and main-streaming of knot theory.Ralph Fox attended Swarthmore...
asks if the converse is true: is every slice knot ribbon?
Morse-theoretic formulation
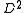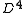A slice disc M is a smoothly embedded in with 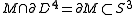. Consider the function given by 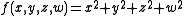. By a small isotopy of M one can ensure that f restricts to a Morse function on M. One says 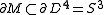is a ribbon knot if has no local maxima.