Winding number - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, the winding number of a closed curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

in the plane

Plane (mathematics)

In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...

around a given point is an integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

representing the total number of times that curve travels counterclockwise around the point. The winding number depends on the orientation

Curve orientation

In mathematics, a positively oriented curve is a planar simple closed curve such that when traveling on it one always has the curve interior to the left...

of the curve, and is negative if the curve travels around the point clockwise.

Winding numbers are fundamental objects of study in algebraic topology

Algebraic topology

Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...

, and they play an important role in vector calculus, complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

, geometric topology

Geometric topology

In mathematics, geometric topology is the study of manifolds and maps between them, particularly embeddings of one manifold into another.- Topics :...

, differential geometry, and physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

, including string theory

String theory

String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...

Intuitive description

Suppose we are given a closed, oriented curve in the xy plane. We can imagine the curve as the path of motion of some object, with the orientation indicating the direction in which the object moves. Then the winding number of the curve is equal to the total number of counterclockwise turns

Turn (geometry)

A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....

that the object makes around the origin.

When counting the total number of turns

Turn (geometry)

A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....

, counterclockwise motion counts as positive, while clockwise motion counts as negative. For example, if the object first circles the origin four times counterclockwise, and then circles the origin once clockwise, then the total winding number of the curve is three.

Using this scheme, a curve that does not travel around the origin at all has winding number zero, while a curve that travels clockwise around the origin has negative winding number. Therefore, the winding number of a curve may be any integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

. The following pictures show curves with winding numbers between −2 and 3:


−2	−1	0

1	2	3

Formal definition

A curve in the xy plane can be defined by parametric equation

Parametric equation

In mathematics, parametric equation is a method of defining a relation using parameters. A simple kinematic example is when one uses a time parameter to determine the position, velocity, and other information about a body in motion....

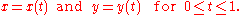
If we think of the parameter t as time, then these equations specify the motion of an object in the plane between and . The path of this motion is a curve as long as the functions

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

x(t) and y(t) are continuous

Continuous function

In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...

. This curve is closed as long as the position of the object is the same at and .

We can define the winding number of such a curve using the polar coordinate system

Polar coordinate system

In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....

. Assuming the curve does not pass through the origin, we can rewrite the parametric equations in polar form:

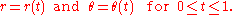
The functions r(t) and θ(t) are required to be continuous, with . Because the initial and final positions are the same, θ(0) and θ(1) must differ by an integer multiple of 2π. This integer is the winding number:

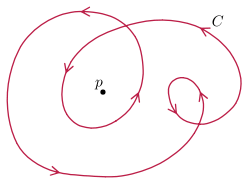
This defines the winding number of a curve around the origin in the xy plane. By translating the coordinate system, we can extend this definition to include winding numbers around any point p.

Alternative definitions

Winding number is often defined in different ways in various parts of mathematics. All of the definitions below are equivalent to the one given above:

Differential geometry

In differential geometry, parametric equations are usually assumed to be differentiable (or at least piecewise differentiable). In this case, the polar coordinate θ is related to the rectangular coordinates x and y by the equation: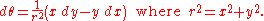

By the fundamental theorem of calculus

Fundamental theorem of calculus

The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...

, the total change in θ is equal to the integral

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

of dθ. We can therefore express the winding number of a differentiable curve as a line integral

Line integral

In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...

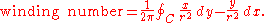
The one-form

One-form

In linear algebra, a one-form on a vector space is the same as a linear functional on the space. The usage of one-form in this context usually distinguishes the one-forms from higher-degree multilinear functionals on the space. For details, see linear functional.In differential geometry, a...

dθ (defined on the complement of the origin) is closed

Closed and exact differential forms

In mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero , and an exact form is a differential form that is the exterior derivative of another differential form β...

but not exact, and it generates the first De Rham cohomology

De Rham cohomology

In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...

group of the punctured plane. In particular, if ω is any closed differentiable one-form defined on the complement of the origin, then the integral of ω along closed loops gives a multiple of the winding number.

Complex analysis

In complex analysis

Complex analysis

, the winding number of a closed curve C in the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

can be expressed in terms of the complex coordinate . Specifically, if we write z = re^iθ, then

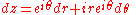
and therefore

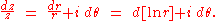
The total change in ln(r) is zero, and thus the integral of dz ⁄ z is equal to i multiplied by the total change in θ. Therefore:

More generally, the winding number of C around any complex number a is given by

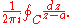
This is a special case of the famous Cauchy integral formula. Winding numbers play a very important role throughout complex analysis (c.f. the statement of the residue theorem

Residue theorem

The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...

Topology

In topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

, the winding number is an alternate term for the degree of a continuous mapping

Degree of a continuous mapping

In topology, the degree is a numerical invariant that describes a continuous mapping between two compact oriented manifolds of the same dimension. Intuitively, the degree represents the number of times that the domain manifold wraps around the range manifold under the mapping...

. In physics

Physics

, winding numbers are frequently called topological quantum number

Topological quantum number

In physics, a topological quantum number is any quantity, in a physical theory, that takes on only one of a discrete set of values, due to topological considerations...

s. In both cases, the same concept applies.

The above example of a curve winding around a point has a simple topological interpretation. The complement of a point in the plane is homotopy equivalent to the circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

, such that maps from the circle to itself are really all that need to be considered. It can be shown that each such map can be continuously deformed to (is homotopic to) one of the standard maps

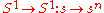, where multiplication in the circle is defined by identifying it with the complex unit circle. The set of homotopy classes of maps from a circle to a topological space

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

is called the first homotopy group

Homotopy group

In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...

or fundamental group

Fundamental group

In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...

of that space. The fundamental group of the circle is the integers Z and the winding number of a complex curve is just its homotopy class.

Maps from the 3-sphere to itself are also classified by an integer which is also called the winding number or sometimes Pontryagin index.

Polygons

In polygon

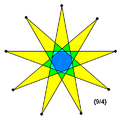
Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

s, the winding number is referred to as the polygon density. For convex polygons, and more generally simple polygon

Simple polygon

In geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....

s (not self-intersecting), the density is 1, by the Jordan curve theorem

Jordan curve theorem

In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...

. By contrast, for a regular star polygon {p/q}, the density is q.

Turning number

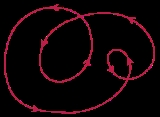
One can also consider the winding number of the path with respect to the tangent of the path itself. As a path followed through time, this would be the winding number with respect to the origin of the velocity vector. In this case the example illustrated on the right has a winding number of 4 (or −4), because the small loop is counted.

This is only defined for immersed paths (i.e., for differentiable paths with nowhere vanishing derivatives), and is the degree of the tangential Gauss map

Gauss map

In differential geometry, the Gauss map maps a surface in Euclidean space R3 to the unit sphere S2. Namely, given a surface X lying in R3, the Gauss map is a continuous map N: X → S2 such that N is a unit vector orthogonal to X at p, namely the normal vector to X at p.The Gauss map can be defined...

.

This is called the turning number, and can be computed as the total curvature

Total curvature

In mathematical study of the differential geometry of curves, the total curvature of an immersed plane curve is the integral of curvature along a curve taken with respect to arclength:\int_a^b k\,ds....

divided by 2π.

Winding number and Heisenberg ferromagnet equations

Finally, note that the winding number is closely related with the (2 + 1)-dimensional continuous Heisenberg ferromagnet equations and its integrable extensions: the Ishimori equation

Ishimori equation

The Ishimori equation is a partial differential equation proposed by the Japanese mathematician . Its interest is as the first example of a nonlinear spin-one field model in the plane that is integrable .-Equation:The IE has the form...

etc. Solutions of the last equations are classified by the winding number or topological charge (topological invariant and/or topological quantum number

Topological quantum number

In physics, a topological quantum number is any quantity, in a physical theory, that takes on only one of a discrete set of values, due to topological considerations...

Intuitive description

Formal definition

Alternative definitions

Differential geometry

Complex analysis

Topology

Polygons

Turning number

Winding number and Heisenberg ferromagnet equations

See also