Residue theorem

The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis

Complex analysis

Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...

 is a powerful tool to evaluate line integral

Line integral

In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...

s of analytic function

Analytic function

In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...

s over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula

Cauchy's integral formula

In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all...

. From a geometrical perspective, it is a special case of the generalized Stokes' theorem

Stokes' theorem

In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...

.

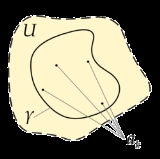
The statement is as follows. Suppose U is a simply connected open subset of the complex plane

Complex plane

In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...

, and a₁,...,a_n are finitely many points of U and f is a function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 which is defined and holomorphic

Holomorphic function

In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...

 on U \ {a₁,...,a_n}. If γ is a rectifiable curve in U which does not meet any of the a_k, and whose start point equals its endpoint, then


If γ is a positively oriented

Curve orientation

In mathematics, a positively oriented curve is a planar simple closed curve such that when traveling on it one always has the curve interior to the left...

 Jordan curve, I(γ, a_k) = 1
if a_k is in the interior of γ, and 0 if not, so
with the sum over those k for which a_k is inside γ.

Here, Res(f, a_k) denotes the residue

Residue (complex analysis)

In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...

 of f at a_k, and I(γ, a_k) is the winding number

Winding number

In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...

 of the curve γ about the point a_k. This winding number is an integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

 which intuitively measures how many times the curve γ winds around the point a_k; it is positive if γ moves in a counter clockwise ("mathematically positive") manner around a_k and 0 if γ doesn't move around a_k at all.

The relationship of the residue theorem to Stokes' theorem is given by the Jordan curve theorem

Jordan curve theorem

In topology, a Jordan curve is a non-self-intersecting continuous loop in the plane, and another name for a Jordan curve is a "simple closed curve"...

. The general plane curve

Plane curve

In mathematics, a plane curve is a curve in a Euclidean plane . The most frequently studied cases are smooth plane curves , and algebraic plane curves....

 γ must first be reduced to a set of simple closed curves {γ_i} whose total is equivalent to γ for integration purposes; this reduces the problem to finding the integral of f dz along a Jordan curve γ_i with interior V. The requirement that f be holomorphic on U₀ = U \ {a_k} is equivalent to the statement that the exterior derivative

Exterior derivative

In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....

 d(f dz) = 0 on U₀. Thus if two planar regions V and W of U enclose the same subset {a_j} of {a_k}, the regions V\W and W\V lie entirely in U₀, and hence is well-defined and equal to zero. Consequently, the contour integral of f dz along γ_i=∂V is equal to the sum of a set of integrals along paths λ_j, each enclosing an arbitrarily small region around a single a_j—the residues of f (up to the conventional factor 2πi) at {a_j}. Summing over {γ_i}, we recover the final expression of the contour integral in terms of the winding numbers {I(γ, a_k)}.

In order to evaluate real integrals, the residue theorem is used in the following manner: the integrand is extended to the complex plane and its residues are computed (which is usually easy), and a part of the real axis is extended to a closed curve by attaching a half-circle in the upper or lower half-plane, forming a semicircle. The integral over this curve can then be computed using the residue theorem. Often, the half-circle part of the integral will tend towards zero as the radius of the half-circle grows, leaving only the real-axis part of the integral, the one we were originally interested in.

Example

The integral


arises in probability theory

Probability theory

Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...

 when calculating the characteristic function

Characteristic function (probability theory)

In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...

 of the Cauchy distribution

Cauchy distribution

The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...

. It resists the techniques of elementary calculus

Calculus

Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...

 but can be evaluated by expressing it as a limit of contour integrals.

Suppose t > 0 and define the contour C that goes along the real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

line from −a to a and then counterclockwise along
a semicircle centered at 0 from a to −a. Take
a to be greater than 1, so that the imaginary

Imaginary number

An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...

unit i is enclosed within the curve. The contour integral is


Since e^itz is an entire function

Entire function

In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...

(having no singularities

Mathematical singularity

In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...

at any point in the complex plane), this function has
singularities only where the denominator
z² + 1 is zero. Since
z² + 1 = (z + i)(z − i),
that happens only where z = i or z = −i.
Only one of those points is in the region bounded by this
contour.
Because f(z) is


the residue

Residue (complex analysis)

In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...

 of
f(z) at z = i is


According to the residue theorem, then, we have


The contour C may be split into a "straight"
part and a curved arc, so that


and thus


Using some estimations

Estimation lemma

In mathematics, the estimation lemma gives an upper bound for a contour integral. If f is a complex-valued, continuous function on the contour \Gamma and if its absolute value |f| is bounded by a constant M for all z on \Gamma, then...

, we have


Note that, since t > 0 and for complex numbers in the upper halfplane the argument lies between 0 an , one can estimate


Therefore


If t < 0 then a similar argument with an arc C' that winds around −i
rather than i shows that


and finally we have


(If t = 0 then the integral yields immediately to elementary calculus methods and its value is π.)

See also

• Jordan's lemma
  Jordan's lemma
  In complex analysis, Jordan's lemma is a result frequently used in conjunction with the residue theorem to evaluate contour integrals and improper integrals...
  
  
• Methods of contour integration
  Methods of contour integration
  In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.Contour integration is closely related to the calculus of residues, a methodology of complex analysis....
  
  
• Morera's theorem
  Morera's theorem
  In complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic....
  
  
• Nachbin's theorem
  Nachbin's theorem
  In mathematics, in the area of complex analysis, Nachbin's theorem is commonly used to establish a bound on the growth rates for an analytic function. This article will provide a brief review of growth rates, including the idea of a function of exponential type...
  
  
• Residue at infinity
• Logarithmic form
  Logarithmic form
  In contexts including complex manifolds and algebraic geometry, a logarithmic differential form is a meromorphic differential form with poles of a certain kind....
  
  

External links

• Residue theorem in MathWorld
  MathWorld
  MathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
  
  
• Residue Theorem Module by John H. Mathews