In differential geometry, the Gauss map (named after Carl F. Gauss

Carl Friedrich Gauss

Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...

) maps a surface

Surface

In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

 in Euclidean space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

 R³ to the unit sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

 S². Namely, given a surface X lying in R³, the Gauss map is a continuous map N: X → S² such that N(p) is a unit vector orthogonal to X at p, namely the normal vector to X at p.

The Gauss map can be defined (globally) if and only if the surface is orientable, in which case its degree is half the Euler characteristic

Euler characteristic

In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

. The Gauss map can always be defined locally (i.e. on a small piece of the surface). The Jacobian determinant of the Gauss map is equal to Gaussian curvature

Gaussian curvature

In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...

, and the differential

Differential (calculus)

In calculus, a differential is traditionally an infinitesimally small change in a variable. For example, if x is a variable, then a change in the value of x is often denoted Δx . The differential dx represents such a change, but is infinitely small...

 of the Gauss map is called the shape operator.

Gauss first wrote a draft on the topic in 1825 and published in 1827.

There is also a Gauss map for a link

Link (knot theory)

In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...

, which computes linking number

Linking number

In mathematics, the linking number is a numerical invariant that describes the linking of two closed curves in three-dimensional space. Intuitively, the linking number represents the number of times that each curve winds around the other...

.

Generalizations

The Gauss map can be defined for hypersurface

Hypersurface

In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...

s in Rⁿ as a map from a hypersurface to the unit sphere S^{n − 1} ∈ Rⁿ.

For a general oriented k-submanifold

Submanifold

In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...

 of Rⁿ the Gauss map can be also be defined, and its target space is the oriented Grassmannian

Grassmannian

In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...

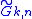, i.e. the set of all oriented k-planes in Rⁿ. In this case a point on the submanifold is mapped to its oriented tangent subspace. One can also map to its oriented normal subspace; these are equivalent as via orthogonal complement.
In Euclidean 3-space

Euclidean space

In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...

, this says that an oriented 2-plane is characterized by an oriented 1-line, equivalently a unit normal vector (as ), hence this is consistent with the definition above.

Finally, the notion of Gauss map can be generalized to an oriented submanifold X of dimension k in an oriented ambient Riemannian manifold

Riemannian manifold

In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...

 M of dimension n. In that case, the Gauss map then goes from X to the set of tangent k-planes in the tangent bundle

Tangent bundle

In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...

 TM. The target space for the Gauss map N is a Grassmann bundle built on the tangent bundle TM. In the case where 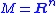, the tangent bundle is trivialized (so the Grassmann bundle becomes a map to the Grassmannian), and we recover the previous definition.

Total curvature

The area of the image of the Gauss map is called the total curvature and is equivalent to the surface integral

Surface integral

In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...

 of the Gaussian curvature

Gaussian curvature

In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...

. This is the original interpretation given by Gauss. The Gauss-Bonnet theorem links total curvature of a surface to its topological

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

 properties.

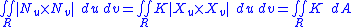
Cusps of the Gauss map

The Gauss map reflects many properties of the surface: when the surface has zero Gaussian curvature, (that is along a parabolic line) the Gauss map will have a fold catastrophe. This fold may contain cusps and these cusps were studied in depth by Thomas Banchoff

Thomas Banchoff

Thomas Francis Banchoff is an American mathematicianspecializing in geometry. He is a professor at Brown University, where he has taught since 1967...

, Terence Gaffney and Clint McCrory. Both parabolic lines and cusp are stable phenomena and will remain under slight deformations of the surface. Cusps occur when:

1. The surface has a bi-tangent plane
2. A ridge crosses a parabolic line
3. at the closure of the set of inflection points of the asymptotic curves of the surface.

There are two types of cusp: elliptic cusp and hyperbolic cusps.