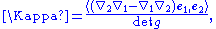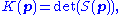Gaussian curvature - AbsoluteAstronomy.com

In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface

Surface

In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...

is the product of the principal curvature

Principal curvature

In differential geometry, the two principal curvatures at a given point of a surface are the eigenvalues of the shape operator at the point. They measure how the surface bends by different amounts in different directions at that point.-Discussion:...

s, κ₁ and κ₂, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way it is isometrically embedded

Embedding

In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....

in space. This result is the content of Gauss's

Carl Friedrich Gauss

Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...

Theorema egregium

Theorema Egregium

Gauss's Theorema Egregium is a foundational result in differential geometry proved by Carl Friedrich Gauss that concerns the curvature of surfaces...

.

Symbolically, the Gaussian curvature

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

Κ is defined as

.
where

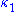and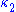

are the principal curvatures

Principal curvature

Alternative definitions

It is also given by

where

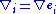is the covariant derivative

Covariant derivative

In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...

and g is the metric tensor

Metric tensor

In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...

.

At a point p on a regular surface in R³, the Gaussian curvature is also given by

where S is the shape operator.

A useful formula for the Gaussian curvature is Liouville's equation in terms of the Laplacian in isothermal coordinates

Isothermal coordinates

In mathematics, specifically in differential geometry, isothermal coordinates on a Riemannian manifoldare local coordinates where the metric isconformal to the Euclidean metric...

Informal definition

We represent the surface by the implicit function theorem

Implicit function theorem

In multivariable calculus, the implicit function theorem is a tool which allows relations to be converted to functions. It does this by representing the relation as the graph of a function. There may not be a single function whose graph is the entire relation, but there may be such a function on...

as the graph of a function, f, of two variables, in such a way that the point p is a critical point, i.e., the gradient of f vanishes (this can always be attained by a suitable rigid motion). Then the Gaussian curvature of the surface at p is the determinant of the Hessian matrix

Hessian matrix

In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...

of f (being the product of the eigenvalues of the Hessian). (Recall that the Hessian is the 2-by-2 matrix of second derivatives.) This definition allows one immediately to grasp the distinction between cup/cap versus saddle point.

Total curvature

The surface integral

Surface integral

In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...

of the Gaussian curvature over some region of a surface is called the total curvature. The total curvature of a geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

triangle

Triangle

A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....

equals the deviation of the sum of its angles from

. The sum of the angles of a triangle on a surface of positive curvature will exceed

, while the sum of the angles of a triangle on a surface of negative curvature will be less than

. On a surface of zero curvature, such as the Euclidean plane, the angles will sum to precisely

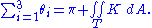
A more general result is the Gauss–Bonnet theorem

Gauss–Bonnet theorem

The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their geometry to their topology...

Theorema egregium

Gauss's Theorema Egregium (Latin: "remarkable theorem") states that Gaussian curvature of a surface can be determined from the measurements of length on the surface itself. In fact, it can be found given the full knowledge of the first fundamental form

First fundamental form

In differential geometry, the first fundamental form is the inner product on the tangent space of a surface in three-dimensional Euclidean space which is induced canonically from the dot product of R3. It permits the calculation of curvature and metric properties of a surface such as length and...

and expressed via the first fundamental form and its partial derivative

Partial derivative

In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...

s of first and second order. Equivalently, the determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

of the second fundamental form of a surface in R³ can be so expressed. The "remarkable", and surprising, feature of this theorem is that although the definition of the Gaussian curvature of a surface S in R³ certainly depends on the way in which the surface is located in space, the end result, the Gaussian curvature itself, is determined by the inner metric of the surface without any further reference to the ambient space: it is an intrinsic invariant

Invariant (mathematics)

In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...

. In particular, the Gaussian curvature is invariant under isometric

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

deformations of the surface.

In contemporary differential geometry, a "surface", viewed abstractly, is a two-dimensional differentiable manifold

Differentiable manifold

A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...

. To connect this point of view with the classical theory of surfaces

Differential geometry of surfaces

In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....

, such an abstract surface is embedded

Embedding

In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....

into R³ and endowed with the Riemannian metric given by the first fundamental form. Suppose that the image of the embedding is a surface S in R³. A local isometry is a diffeomorphism

Diffeomorphism

In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...

f: U → V between open regions of R³ whose restriction to S ∩ U is an isometry

Isometry

onto its image. Theorema Egregium is then stated as follows:

The Gaussian curvature of an embedded smooth surface in R³ is invariant under the local isometries.

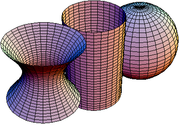
For example, the Gaussian curvature of a cylindrical

Cylinder (geometry)

A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...

tube is zero, the same as for the "unrolled" tube (which is flat). On the other hand, since a sphere

Sphere

A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

of radius R has constant positive curvature R⁻² and a flat plane has constant curvature 0, these two surfaces are not isometric, even locally. Thus any planar representation of even a part of a sphere must distort the distances. Therefore, no cartographic projection is perfect.

Gauss–Bonnet theorem

The Gauss-Bonnet theorem links the total curvature of a surface to its Euler characteristic

Euler characteristic

In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

and provides an important link between local geometric properties and global topological properties.

Surfaces of constant curvature

Minding
Ferdinand Minding
Ferdinand Minding was a German–Russian mathematician known for his contributions to differential geometry. He continued the work of Gauss concerning differential geometry of surfaces, especially its intrinsic aspects. Minding considered questions of bending of surfaces and proved the invariance of...

's theorem (1839) states that all surfaces with the same constant curvature K are locally isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

. A consequence of Minding's theorem is that any surface whose curvature is identically zero can be constructed by bending some plane region. Such surfaces are called developable surface
Developable surface
In mathematics, a developable surface is a surface with zero Gaussian curvature. That is, it is a "surface" that can be flattened onto a plane without distortion . Conversely, it is a surface which can be made by transforming a plane...

s. Minding also raised the question whether a closed surface with constant positive curvature is necessarily rigid.

Liebmann's theorem (1900) answered Minding's question. The only regular (of class C²) closed surfaces in R³ with constant positive Gaussian curvature are sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...

s.

Hilbert's theorem (1901) states that there exists no complete analytic (class C^ω) regular surface in R³ of constant negative Gaussian curvature. In fact, the conclusion also holds for surfaces of class C² immersed in R³, but breaks down for C¹-surfaces. The pseudosphere
Pseudosphere
In geometry, the term pseudosphere is used to describe various surfaces with constant negative gaussian curvature. Depending on context, it can refer to either a theoretical surface of constant negative curvature, to a tractricoid, or to a hyperboloid....

has constant negative Gaussian curvature except at its singular cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....

.

Alternative Formulas

Gaussian curvature of a surface in R³ can be expressed as the ratio of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

s of the second and first
First fundamental form
In differential geometry, the first fundamental form is the inner product on the tangent space of a surface in three-dimensional Euclidean space which is induced canonically from the dot product of R3. It permits the calculation of curvature and metric properties of a surface such as length and...

fundamental forms:

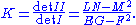
The Brioschi formula gives Gaussian curvature solely in terms of the first fundamental form:

For an orthogonal
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...

parametrization, Gaussian curvature is: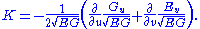

For a surface described as graph of a function 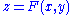, Gaussian curvature is: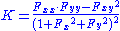

For a surface 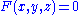, Gaussian curvature is:

Gaussian curvature is the limiting difference between the circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....

of a geodesic circle and a circle in the plane: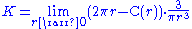

Gaussian curvature is the limiting difference between the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...

of a geodesic disk and a disk in the plane:

Gaussian curvature may be expressed with the Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...

:

External links

Curvature in two spacelike dimensions

Alternative definitions

Informal definition

Total curvature

Theorema egregium

Gauss–Bonnet theorem

Surfaces of constant curvature

Alternative Formulas

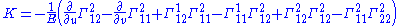
External links

See also