
Isothermal coordinates
Encyclopedia
In mathematics
, specifically in differential geometry, isothermal coordinates on a Riemannian manifold
are local coordinates where the metric
is
conformal
to the Euclidean metric. This means that in isothermal
coordinates, the Riemannian metric locally has the form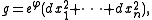
where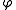 is a smooth function
is a smooth function
.
Isothermal coordinates on surfaces were first introduced by Gauss
. Korn and Lichtenstein proved that isothermal coordinates exist around any point on a two dimensional Riemannian manifold. On higher dimensional Riemannian manifolds a necessary and sufficient condition for their local existence is the vanishing of the Weyl tensor
and of the Cotton tensor
.
and Zygmund
. A simpler approach to the Beltrami equation has been given more recently by the late Adrien Douady
.
If the Riemannian metric is given locally as
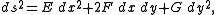
then in the complex coordinate z = x + iy, it takes the form

where λ and μ are smooth with λ > 0 and |μ| < 1. In fact
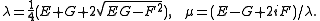
In isothermal coordinates (u, v) the metric should take the form
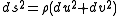
with ρ > 0 smooth. The complex coordinate w = u + i v satisfies
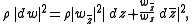
so that the coordinates (u, v) will be isothermal if the Beltrami equation

has a diffeomorphic solution. Such a solution has been proved to exist in any neighbourhood where ||μ||∞ < 1.

where is the Hodge star operator defined by the metric.
is the Hodge star operator defined by the metric.
Let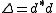 be the Laplace–Beltrami operator on functions.
be the Laplace–Beltrami operator on functions.
Then by standard elliptic theory, u can be chosen to be harmonic
near a given point, i.e. Δ u = 0, with du non-vanishing.
By the Poincaré lemma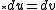 has a local solution v exactly when
has a local solution v exactly when 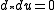 .
.
Since
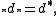
this is equivalent to Δ u = 0, and hence a local solution exists.
Since du is non-zero and the square of the Hodge star operator is −1 on 1-forms, du and dv are necessarily linearly independent, and therefore give local isothermal coordinates.
takes the simpler form
where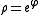 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in differential geometry, isothermal coordinates on a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
are local coordinates where the metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
is
conformal
Conformal
Conformal may refer to:* Conformal map, in mathematics* Conformal geometry, in mathematics* Conformal map projection, in cartography* Conformal film on a surface* Conformal coating in electronics* Conformal hypergraph, in mathematics...
to the Euclidean metric. This means that in isothermal
coordinates, the Riemannian metric locally has the form
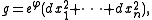
where
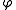 is a smooth function
is a smooth functionSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
.
Isothermal coordinates on surfaces were first introduced by Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
. Korn and Lichtenstein proved that isothermal coordinates exist around any point on a two dimensional Riemannian manifold. On higher dimensional Riemannian manifolds a necessary and sufficient condition for their local existence is the vanishing of the Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
and of the Cotton tensor
Cotton tensor
In differential geometry, the Cotton tensor on a -Riemannian manifold of dimension n is a third-order tensor concomitant of the metric, like the Weyl tensor. The concept is named after Émile Cotton...
.
Isothermal coordinates on surfaces
The first result on the existence of isothermal coordinates was due to and . Later accounts were given by , , and . A particularly simple account using the Hodge star operator is given in .Beltrami equation
The existence of isothermal coordinates can be proved by applying known existence theorems for the Beltrami equation, which rely on Lp estimates for singular integral operators of CalderonAlberto Calderón
Alberto Pedro Calderón was an Argentine mathematician best known for his work on the theory of partial differential equations and singular integral operators, and widely considered as one of the 20th century's most important mathematicians...
and Zygmund
Antoni Zygmund
Antoni Zygmund was a Polish-born American mathematician.-Life:Born in Warsaw, Zygmund obtained his PhD from Warsaw University and became a professor at Stefan Batory University at Wilno...
. A simpler approach to the Beltrami equation has been given more recently by the late Adrien Douady
Adrien Douady
Adrien Douady was a French mathematician.He was a student of Henri Cartan at the Ecole Normale Supérieure, and initially worked in homological algebra. His thesis concerned deformations of complex analytic spaces...
.
If the Riemannian metric is given locally as
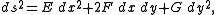
then in the complex coordinate z = x + iy, it takes the form

where λ and μ are smooth with λ > 0 and |μ| < 1. In fact
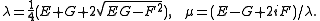
In isothermal coordinates (u, v) the metric should take the form
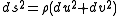
with ρ > 0 smooth. The complex coordinate w = u + i v satisfies
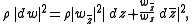
so that the coordinates (u, v) will be isothermal if the Beltrami equation

has a diffeomorphic solution. Such a solution has been proved to exist in any neighbourhood where ||μ||∞ < 1.
Hodge star operator
New coordinates u and v are isothermal provided that
where
 is the Hodge star operator defined by the metric.
is the Hodge star operator defined by the metric.Let
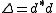 be the Laplace–Beltrami operator on functions.
be the Laplace–Beltrami operator on functions.Then by standard elliptic theory, u can be chosen to be harmonic
Harmonic
A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...
near a given point, i.e. Δ u = 0, with du non-vanishing.
By the Poincaré lemma
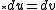 has a local solution v exactly when
has a local solution v exactly when 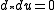 .
.Since
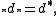
this is equivalent to Δ u = 0, and hence a local solution exists.
Since du is non-zero and the square of the Hodge star operator is −1 on 1-forms, du and dv are necessarily linearly independent, and therefore give local isothermal coordinates.
Gaussian curvature
In the isothermal coordinates (u, v), the Gaussian curvatureGaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
takes the simpler form
where
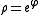 .
.


