
Cotton tensor
Encyclopedia
In differential geometry, the Cotton tensor on a (pseudo)-Riemannian manifold
of dimension n is a third-order tensor
concomitant of the metric
, like the Weyl tensor. The concept is named after Émile Cotton. Just as the vanishing of the Weyl tensor for n ≥ 4 is a necessary and sufficient condition for the manifold to be conformally flat
, the same is true for the Cotton tensor for n = 3, while for n < 3 it is identically zero.
In coordinates, and denoting the Ricci tensor by Rij and the scalar curvature by R, the components of the Cotton tensor are

The Cotton tensor can be regarded as a vector valued 2-form
, and for n=3 one can use the Hodge star operator to convert this in to a second order trace free tensor density
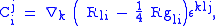
sometimes called the Cotton–York tensor.
The proof of the classical result that for n = 3 the vanishing of the Cotton tensor is equivalent the metric being conformally flat is given by Eisenhart
using a standard integrability argument. This tensor density is uniquely characterized by its conformal properties coupled with the demand that it be differentiable for arbitrary metrics, as shown by Aldersley.
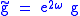 for some scalar function
for some scalar function  the Cotton-York tensor transforms as
the Cotton-York tensor transforms as
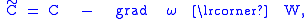
where the gradient is plugged into the symmetric part of the Weyl tensor
W.
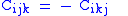
and therefore

In addition the Bianchi formula for the Weyl tensor
for can be rewritten as
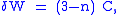
where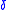 is the positive divergence in the first component of W.
is the positive divergence in the first component of W.
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
of dimension n is a third-order tensor
Tensor field
In mathematics, physics and engineering, a tensor field assigns a tensor to each point of a mathematical space . Tensor fields are used in differential geometry, algebraic geometry, general relativity, in the analysis of stress and strain in materials, and in numerous applications in the physical...
concomitant of the metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
, like the Weyl tensor. The concept is named after Émile Cotton. Just as the vanishing of the Weyl tensor for n ≥ 4 is a necessary and sufficient condition for the manifold to be conformally flat
Conformally flat
A Riemannian manifold is conformally flat if each point has a neighborhood that can be mapped to flat space by a conformal transformation.More formally, let be a pseudo-Riemannian manifold...
, the same is true for the Cotton tensor for n = 3, while for n < 3 it is identically zero.
In coordinates, and denoting the Ricci tensor by Rij and the scalar curvature by R, the components of the Cotton tensor are

The Cotton tensor can be regarded as a vector valued 2-form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
, and for n=3 one can use the Hodge star operator to convert this in to a second order trace free tensor density
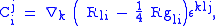
sometimes called the Cotton–York tensor.
The proof of the classical result that for n = 3 the vanishing of the Cotton tensor is equivalent the metric being conformally flat is given by Eisenhart
Luther P. Eisenhart
Luther Pfahler Eisenhart was an American mathematician, best known today for his contributions to semi-Riemannian geometry.-Life:...
using a standard integrability argument. This tensor density is uniquely characterized by its conformal properties coupled with the demand that it be differentiable for arbitrary metrics, as shown by Aldersley.
Conformal rescaling
Under conformal rescaling of the metric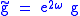 for some scalar function
for some scalar function  the Cotton-York tensor transforms as
the Cotton-York tensor transforms as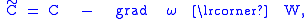
where the gradient is plugged into the symmetric part of the Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
W.
Symmetries
The Cotton tensor has the following symmetries: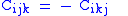
and therefore

In addition the Bianchi formula for the Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
for can be rewritten as
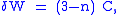
where
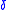 is the positive divergence in the first component of W.
is the positive divergence in the first component of W.

