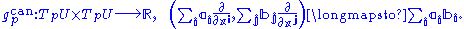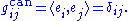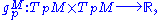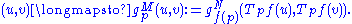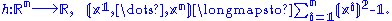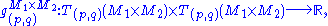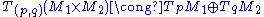Riemannian manifold
Encyclopedia
In Riemannian geometry
and the differential geometry of surfaces
, a Riemannian manifold or Riemannian space (M,g) is a real differentiable manifold
M in which each tangent space
is equipped with an inner product
g, a Riemannian metric, which varies smoothly from point to point. The terms are named after German mathematician Bernhard Riemann
.
A Riemannian metric makes it possible to define various geometric notions on a Riemannian manifold, such as angle
s, lengths of curve
s, area
s (or volume
s), curvature
, gradient
s of functions and divergence
of vector field
s.
proved his Theorema Egregium
(remarkable theorem in Latin), establishing an important property of surfaces. Informally, the theorem says that the curvature of a surface
can be determined entirely by measuring distances along paths on the surface. That is, curvature does not depend on how the surface might be embedded in 3-dimensional space. See differential geometry of surfaces
. Bernhard Riemann
extended Gauss's theory to higher dimensional spaces called manifolds in a way that also allows distances and angles to be measured and the notion of curvature to be defined, again in a way that was intrinsic to the manifold and not dependent upon its embedding in higher-dimensional spaces. Albert Einstein
used the theory of Riemannian manifolds to develop his General Theory of Relativity. In particular, his equations for gravitation are restrictions on the curvature of space.
of a smooth manifold M assigns to each fixed point of M a vector space called the tangent space
, and each tangent space can be equipped with an inner product. If such a collection of inner products on the tangent bundle of a manifold varies smoothly as one traverses the manifold, then concepts that were defined only pointwise at each tangent space can be extended to yield analogous notions over finite regions of the manifold. For example, a smooth curve
α(t): [0, 1] → M has tangent vector α′(t0) in the tangent space TM(α(t0)) at any point t0 ∈ (0, 1), and each such vector has length ‖α′(t0)‖, where ‖·‖ denotes the norm
induced by the inner product on TM(α(t0)). The integral
of these lengths gives the length of the curve α:
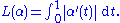
Smoothness of α(t) for t in [0, 1] guarantees that the integral L(α) exists and the length of this curve is defined.
In many instances, in order to pass from a linear-algebraic concept to a differential-geometric one, the smoothness requirement is very important.
Every smooth submanifold
of Rn has an induced Riemannian metric g: the inner product on each tangent space is the restriction of the inner product on Rn. In fact, as follows from the Nash embedding theorem
, all Riemannian manifolds can be realized this way.
In particular one could define Riemannian manifold as a metric space
which is isometric
to a smooth submanifold of Rn with the induced intrinsic metric
, where isometry here is meant in the sense of preserving the length of curves. This definition might theoretically not be flexible enough, but it is quite useful to build the first geometric intuitions in Riemannian geometry
.
of the positive-definite quadratic forms on the tangent bundle
. Then one has to work to show that it can be turned to a metric space:
If γ: [a, b] → M is a continuously differentiable curve
in the Riemannian manifold M, then we define its length L(γ) in analogy with the example above by
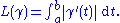
With this definition of length, every connected
Riemannian manifold M becomes a metric space
(and even a length metric space
) in a natural fashion: the distance d(x, y) between the points x and y of M is defined as
Even though Riemannian manifolds are usually "curved," there is still a notion of "straight line" on them: the geodesic
s. These are curves which locally join their points along shortest path
s.
Assuming the manifold is compact, any two points x and y can be connected with a geodesic whose length is d(x,y). Without compactness, this need not be true. For example, in the punctured plane R2 \ {0}, the distance between the points (−1, 0) and (1, 0) is 2, but there is no geodesic realizing this distance.
completeness
, topological
completeness and metric
completeness are the same: that each implies the other is the content of the Hopf-Rinow theorem.
of dimension n. A Riemannian metric on M is a family of (positive definite) inner products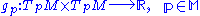
such that, for all differentiable vector fields X,Y on M,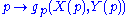
defines a smooth function
M → R.
More formally, a Riemannian metric is a symmetric (0,2)-tensor that is positive definite (i.e. g(X,X) > 0 for all tangent vectors X ≠ 0).
is a symmetric (0,2)-tensor that is positive definite (i.e. g(X,X) > 0 for all tangent vectors X ≠ 0).
In a system of local coordinates
on the manifold M given by n real-valued functions x1,x2, …, xn, the vector fields
give a basis of tangent vector
s at each point of M. Relative to this coordinate system, the components of the metric tensor are, at each point p,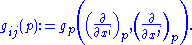
Equivalently, the metric tensor
can be written in terms of the dual basis {dx1, …, dxn} of the cotangent bundle as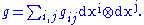
Endowed with this metric, the differentiable manifold
(M,g) is a Riemannian manifold.
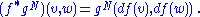
where df(v) is the pushforward of v by f.
The quadratic form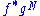 is in general only a semi definite form because
is in general only a semi definite form because 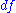 can have a kernel. If f is a diffeomorphism
can have a kernel. If f is a diffeomorphism
, or more generally an immersion, then it defines a Riemannian metric on M, the pullback metric. In particular, every embedded smooth submanifold
inherits a metric from being embedded in a Riemannian manifold, and every covering space inherits a metric from covering a Riemannian manifold.
atlas
of open subsets U of M and diffeomorphisms onto open subsets of Rn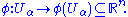
Let τα be a differentiable partition of unity subordinate to the given atlas. Then define the metric g on M by
where gcan is the Euclidean metric. This is readily seen to be a metric on M.
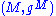 and
and 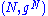 be two Riemannian manifolds, and
be two Riemannian manifolds, and 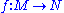 be a diffeomorphism. Then, f is called an isometry, if
be a diffeomorphism. Then, f is called an isometry, if
or pointwise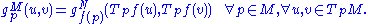
Moreover, a differentiable mapping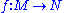 is called a local isometry at
is called a local isometry at 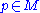 if there is a neighbourhood
if there is a neighbourhood  ,
, 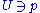 , such that
, such that 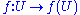 is a diffeomorphism satisfying the previous relation.
is a diffeomorphism satisfying the previous relation.
Riemannian manifold carries the structure of a metric space
whose distance function is the arclength of a minimizing geodesic
.
Specifically, let (M,g) be a connected Riemannian manifold. Let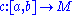 be a parametrized curve in M, which is differentiable with velocity vector c′. The length of c is defined as
be a parametrized curve in M, which is differentiable with velocity vector c′. The length of c is defined as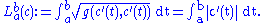
By change of variables
, the arclength is independent of the chosen parametrization. In particular, a curve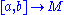 can be parametrized by its arc length. A curve is parametrized by arclength if and only if
can be parametrized by its arc length. A curve is parametrized by arclength if and only if 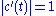 for all
for all 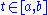 .
.
The distance function d : M×M → [0,∞) is defined by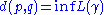
where the infimum
extends over all differentiable curves γ beginning at p∈M and ending at q∈M.
This function d satisfies the properties of a distance function for a metric space. The only property which is not completely straightforward is to show that d(p,q)=0 implies that p=q. For this property, one can use a normal coordinate system
, which also allows one to show that the topology induced by d is the same as the original topology on M.

The diameter is invariant under global isometries. Furthermore, the Heine-Borel property holds for (finite-dimensional) Riemannian manifolds: M is compact
if and only if it is complete and has finite diameter.
 , the exponential map
, the exponential map 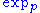 is defined for all
is defined for all 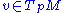 , i.e. if any geodesic
, i.e. if any geodesic 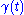 starting from p is defined for all values of the parameter
starting from p is defined for all values of the parameter 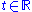 . The Hopf-Rinow theorem asserts that M is geodesically complete if and only if it is complete as a metric space.
. The Hopf-Rinow theorem asserts that M is geodesically complete if and only if it is complete as a metric space.
If M is complete, then M is non-extendable in the sense that it is not isometric to an open proper submanifold of any other Riemannian manifold. The converse is not true, however: there exist non-extendable manifolds which are not complete.
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
and the differential geometry of surfaces
Differential geometry of surfaces
In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....
, a Riemannian manifold or Riemannian space (M,g) is a real differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
M in which each tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
is equipped with an inner product
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
g, a Riemannian metric, which varies smoothly from point to point. The terms are named after German mathematician Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
.
A Riemannian metric makes it possible to define various geometric notions on a Riemannian manifold, such as angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s, lengths of curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s, area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
s (or volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
s), curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
, gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
s of functions and divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
s.
Introduction
In 1828, Carl Friedrich GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
proved his Theorema Egregium
Theorema Egregium
Gauss's Theorema Egregium is a foundational result in differential geometry proved by Carl Friedrich Gauss that concerns the curvature of surfaces...
(remarkable theorem in Latin), establishing an important property of surfaces. Informally, the theorem says that the curvature of a surface
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
can be determined entirely by measuring distances along paths on the surface. That is, curvature does not depend on how the surface might be embedded in 3-dimensional space. See differential geometry of surfaces
Differential geometry of surfaces
In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....
. Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
extended Gauss's theory to higher dimensional spaces called manifolds in a way that also allows distances and angles to be measured and the notion of curvature to be defined, again in a way that was intrinsic to the manifold and not dependent upon its embedding in higher-dimensional spaces. Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
used the theory of Riemannian manifolds to develop his General Theory of Relativity. In particular, his equations for gravitation are restrictions on the curvature of space.
Overview
The tangent bundleTangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
of a smooth manifold M assigns to each fixed point of M a vector space called the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
, and each tangent space can be equipped with an inner product. If such a collection of inner products on the tangent bundle of a manifold varies smoothly as one traverses the manifold, then concepts that were defined only pointwise at each tangent space can be extended to yield analogous notions over finite regions of the manifold. For example, a smooth curve
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
α(t): [0, 1] → M has tangent vector α′(t0) in the tangent space TM(α(t0)) at any point t0 ∈ (0, 1), and each such vector has length ‖α′(t0)‖, where ‖·‖ denotes the norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
induced by the inner product on TM(α(t0)). The integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of these lengths gives the length of the curve α:
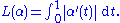
Smoothness of α(t) for t in [0, 1] guarantees that the integral L(α) exists and the length of this curve is defined.
In many instances, in order to pass from a linear-algebraic concept to a differential-geometric one, the smoothness requirement is very important.
Every smooth submanifold
Glossary of differential geometry and topology
This is a glossary of terms specific to differential geometry and differential topology.The following two glossaries are closely related:*Glossary of general topology*Glossary of Riemannian and metric geometry.See also:*List of differential geometry topics...
of Rn has an induced Riemannian metric g: the inner product on each tangent space is the restriction of the inner product on Rn. In fact, as follows from the Nash embedding theorem
Nash embedding theorem
The Nash embedding theorems , named after John Forbes Nash, state that every Riemannian manifold can be isometrically embedded into some Euclidean space. Isometric means preserving the length of every path...
, all Riemannian manifolds can be realized this way.
In particular one could define Riemannian manifold as a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
which is isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
to a smooth submanifold of Rn with the induced intrinsic metric
Intrinsic metric
In the mathematical study of metric spaces, one can consider the arclength of paths in the space. If two points are a given distance from each other, it is natural to expect that one should be able to get from one point to another along a path whose arclength is equal to that distance...
, where isometry here is meant in the sense of preserving the length of curves. This definition might theoretically not be flexible enough, but it is quite useful to build the first geometric intuitions in Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
.
Riemannian manifolds as metric spaces
Usually a Riemannian manifold is defined as a smooth manifold with a smooth sectionSection (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of the positive-definite quadratic forms on the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
. Then one has to work to show that it can be turned to a metric space:
If γ: [a, b] → M is a continuously differentiable curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
in the Riemannian manifold M, then we define its length L(γ) in analogy with the example above by
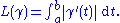
With this definition of length, every connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
Riemannian manifold M becomes a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
(and even a length metric space
Intrinsic metric
In the mathematical study of metric spaces, one can consider the arclength of paths in the space. If two points are a given distance from each other, it is natural to expect that one should be able to get from one point to another along a path whose arclength is equal to that distance...
) in a natural fashion: the distance d(x, y) between the points x and y of M is defined as
- d(x,y) = infInfimumIn mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
{ L(γ) : γ is a continuously differentiable curve joining x and y}.
Even though Riemannian manifolds are usually "curved," there is still a notion of "straight line" on them: the geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s. These are curves which locally join their points along shortest path
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s.
Assuming the manifold is compact, any two points x and y can be connected with a geodesic whose length is d(x,y). Without compactness, this need not be true. For example, in the punctured plane R2 \ {0}, the distance between the points (−1, 0) and (1, 0) is 2, but there is no geodesic realizing this distance.
Properties
In Riemannian manifolds, the notions of geodesicGeodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
completeness
Complete space
In mathematical analysis, a metric space M is called complete if every Cauchy sequence of points in M has a limit that is also in M or, alternatively, if every Cauchy sequence in M converges in M....
, topological
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
completeness and metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
completeness are the same: that each implies the other is the content of the Hopf-Rinow theorem.
Riemannian metrics
Let M be a differentiable manifoldDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
of dimension n. A Riemannian metric on M is a family of (positive definite) inner products
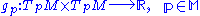
such that, for all differentiable vector fields X,Y on M,
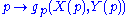
defines a smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
M → R.
More formally, a Riemannian metric
 is a symmetric (0,2)-tensor that is positive definite (i.e. g(X,X) > 0 for all tangent vectors X ≠ 0).
is a symmetric (0,2)-tensor that is positive definite (i.e. g(X,X) > 0 for all tangent vectors X ≠ 0).In a system of local coordinates
Local coordinates
Local coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
on the manifold M given by n real-valued functions x1,x2, …, xn, the vector fields

give a basis of tangent vector
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
s at each point of M. Relative to this coordinate system, the components of the metric tensor are, at each point p,
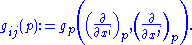
Equivalently, the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
can be written in terms of the dual basis {dx1, …, dxn} of the cotangent bundle as
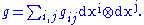
Endowed with this metric, the differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
(M,g) is a Riemannian manifold.
Examples
- With
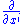 identified with
identified with  , the standard metric over an open subsetOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
, the standard metric over an open subsetOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
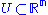 is defined by
is defined by
- Then g is a Riemannian metric, and
- Equipped with this metric, Rn is called Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
of dimension n and gijcan is called the (canonical) Euclidean metric.- Let (M,g) be a Riemannian manifold and
 be a submanifoldSubmanifoldIn mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
be a submanifoldSubmanifoldIn mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
of M. Then the restriction of g to vectors tangent along N defines a Riemannian metric over N. - More generally, let f:Mn→Nn+k be an immersion. Then, if N has a Riemannian metric, f induces a Riemannian metric on M via pullback:
- Let (M,g) be a Riemannian manifold and
- This is then a metric; the positive definiteness follows of the injectivity of the differential of an immersion.
- Let (M,gM) be a Riemannian manifold, h:Mn+k→Nk be a differentiable map and q∈N be a regular value of h (the differential dh(p) is surjective for all p∈h-1(q)). Then h-1(q)⊂M is a submanifold of M of dimension n. Thus h-1(q) carries the Riemannian metric induced by inclusion.
- In particular, consider the following map :
- Then, 0 is a regular value of h and
- is the unit sphere
 . The metric induced from
. The metric induced from 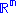 on
on 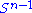 is called the canonical metric of
is called the canonical metric of  .
.
- Let
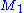 and
and 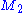 be two Riemannian manifolds and consider the cartesian product
be two Riemannian manifolds and consider the cartesian product 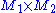 with the product structure. Furthermore, let
with the product structure. Furthermore, let  and
and  be the natural projections. For
be the natural projections. For  , a Riemannian metric on
, a Riemannian metric on 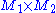 can be introduced as follows :
can be introduced as follows :
- Let
- The identification
- allows us to conclude that this defines a metric on the product space.
- The torus
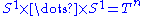 possesses for example a Riemannian structure obtained by choosing the induced Riemannian metric from
possesses for example a Riemannian structure obtained by choosing the induced Riemannian metric from  on the circle
on the circle 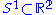 and then taking the product metric. The torus
and then taking the product metric. The torus 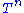 endowed with this metric is called the flat torus.
endowed with this metric is called the flat torus.
- Let
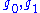 be two metrics on
be two metrics on  . Then,
. Then,
- Let
- is also a metric on M.
The pullback metric
If f:M→N is a differentiable map and (N,gN) a Riemannian manifold, then the pullback of gN along f is a quadratic form on the tangent space of M. The pullback is the quadratic form f*gN on TM defined for v, w ∈ TpM by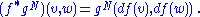
where df(v) is the pushforward of v by f.
The quadratic form
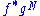 is in general only a semi definite form because
is in general only a semi definite form because 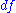 can have a kernel. If f is a diffeomorphism
can have a kernel. If f is a diffeomorphismDiffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
, or more generally an immersion, then it defines a Riemannian metric on M, the pullback metric. In particular, every embedded smooth submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
inherits a metric from being embedded in a Riemannian manifold, and every covering space inherits a metric from covering a Riemannian manifold.
Existence of a metric
Every paracompact differentiable manifold admits a Riemannian metric. To prove this result, let M be a manifold and {(Uα, φ(Uα))|α∈I} a locally finiteLocally finite collection
In the mathematical field of topology, local finiteness is a property of collections of subsets of a topological space. It is fundamental in the study of paracompactness and topological dimension....
atlas
Atlas (topology)
In mathematics, particularly topology, one describesa manifold using an atlas. An atlas consists of individualcharts that, roughly speaking, describe individual regionsof the manifold. If the manifold is the surface of the Earth,...
of open subsets U of M and diffeomorphisms onto open subsets of Rn
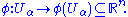
Let τα be a differentiable partition of unity subordinate to the given atlas. Then define the metric g on M by

where gcan is the Euclidean metric. This is readily seen to be a metric on M.
Isometries
Let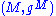 and
and 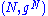 be two Riemannian manifolds, and
be two Riemannian manifolds, and 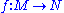 be a diffeomorphism. Then, f is called an isometry, if
be a diffeomorphism. Then, f is called an isometry, if
or pointwise
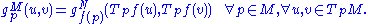
Moreover, a differentiable mapping
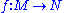 is called a local isometry at
is called a local isometry at 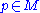 if there is a neighbourhood
if there is a neighbourhood  ,
, 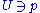 , such that
, such that 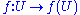 is a diffeomorphism satisfying the previous relation.
is a diffeomorphism satisfying the previous relation.Riemannian manifolds as metric spaces
A connectedConnected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
Riemannian manifold carries the structure of a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
whose distance function is the arclength of a minimizing geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
.
Specifically, let (M,g) be a connected Riemannian manifold. Let
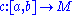 be a parametrized curve in M, which is differentiable with velocity vector c′. The length of c is defined as
be a parametrized curve in M, which is differentiable with velocity vector c′. The length of c is defined as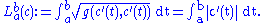
By change of variables
Change of variables
In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with new ones; the new and old variables being related in some specified way...
, the arclength is independent of the chosen parametrization. In particular, a curve
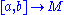 can be parametrized by its arc length. A curve is parametrized by arclength if and only if
can be parametrized by its arc length. A curve is parametrized by arclength if and only if 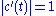 for all
for all 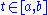 .
.The distance function d : M×M → [0,∞) is defined by
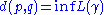
where the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
extends over all differentiable curves γ beginning at p∈M and ending at q∈M.
This function d satisfies the properties of a distance function for a metric space. The only property which is not completely straightforward is to show that d(p,q)=0 implies that p=q. For this property, one can use a normal coordinate system
Normal coordinates
In differential geometry, normal coordinates at a point p in a differentiable manifold equipped with a symmetric affine connection are a local coordinate system in a neighborhood of p obtained by applying the exponential map to the tangent space at p...
, which also allows one to show that the topology induced by d is the same as the original topology on M.
Diameter
The diameter of a Riemannian manifold M is defined by
The diameter is invariant under global isometries. Furthermore, the Heine-Borel property holds for (finite-dimensional) Riemannian manifolds: M is compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
if and only if it is complete and has finite diameter.
Geodesic completeness
A Riemannian manifold M is geodesically complete if for all , the exponential map
, the exponential map 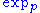 is defined for all
is defined for all 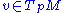 , i.e. if any geodesic
, i.e. if any geodesic 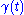 starting from p is defined for all values of the parameter
starting from p is defined for all values of the parameter 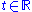 . The Hopf-Rinow theorem asserts that M is geodesically complete if and only if it is complete as a metric space.
. The Hopf-Rinow theorem asserts that M is geodesically complete if and only if it is complete as a metric space.If M is complete, then M is non-extendable in the sense that it is not isometric to an open proper submanifold of any other Riemannian manifold. The converse is not true, however: there exist non-extendable manifolds which are not complete.
See also
- Riemannian geometryRiemannian geometryRiemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
- Finsler manifoldFinsler manifoldIn mathematics, particularly differential geometry, a Finsler manifold is a differentiable manifold together with the structure of an intrinsic quasimetric space in which the length of any rectifiable curve is given by the length functional...
- sub-Riemannian manifoldSub-Riemannian manifoldIn mathematics, a sub-Riemannian manifold is a certain type of generalization of a Riemannian manifold. Roughly speaking, to measure distances in a sub-Riemannian manifold, you are allowed to go only along curves tangent to so-called horizontal subspaces....
- pseudo-Riemannian manifoldPseudo-Riemannian manifoldIn differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
- Metric tensorMetric tensorIn the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
- Hermitian manifoldHermitian manifoldIn mathematics, a Hermitian manifold is the complex analog of a Riemannian manifold. Specifically, a Hermitian manifold is a complex manifold with a smoothly varying Hermitian inner product on each tangent space...
- Space (mathematics)