.gif)
Norm (mathematics)
Encyclopedia
In linear algebra
, functional analysis
and related areas of mathematics
, a norm is a function
that assigns a strictly positive length or size to all vectors in a vector space
, other than the zero vector. A seminorm, on the other hand, is allowed to assign zero length to some non-zero vectors.
A simple example is the 2-dimensional Euclidean space
R2 equipped with the Euclidean norm. Elements in this vector space (e.g., (3, 7)) are usually drawn as arrows in a 2-dimensional cartesian coordinate system
starting at the origin (0, 0). The Euclidean norm assigns to each vector the length of its arrow. Because of this, the Euclidean norm is often known as the magnitude
.
A vector space with a norm is called a normed vector space
. Similarly, a vector space with a seminorm is called a seminormed vector space
.
V over a subfield
F of the complex number
s a norm on V is a function
with the following properties:
For all a ∈ F and all u, v ∈ V,
A simple consequence of the first two axioms, positive homogeneity and the triangle inequality, is p(0) = 0 and thus
A seminorm is a norm with the 3rd property (separating points) removed.
Although every vector space is seminormed (e.g., with the trivial seminorm in the Examples section below), it may not be normed. Every vector space V with seminorm p(v) induces a normed space V/W, called the quotient space
, where W is the subspace of V consisting of all vectors v in V with p(v) = 0. The induced norm on V/W is clearly well-defined and is given by:
A topological vector space
is called normable (seminormable) if the topology
of the space can be induced by a norm (seminorm).
The norm of a vector v is usually denoted ||v||, and sometimes |v|. However, the latter notation is generally discouraged, because it is also used to denote the absolute value
of scalars and the determinant
of matrices.
Rn, the intuitive notion of length of the vector x = (x1, x2, ..., xn) is captured by the formula
This gives the ordinary distance from the origin to the point x, a consequence of the Pythagorean theorem
.
The Euclidean norm is by far the most commonly used norm on Rn, but there are other norms on this vector space as will be shown below. However all these norms are equivalent in the sense that they all define the same topology.
On an n-dimensional complex space
Cn the most common norm is
In both cases we can also express the norm as the square root
of the inner product of the vector and itself:
where x is represented as a column vector ([x1; x2; ...; xn]), and x* denotes its conjugate transpose
.
This formula is valid for any inner product space
, including Euclidean and complex spaces. For Euclidean spaces, the inner product is equivalent to the dot product
. Hence, in this specific case the formula can be also written with the following notation: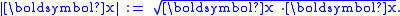
The Euclidean norm is also called the Euclidean length, L2 distance, ℓ2 distance, L2 norm, or ℓ2 norm; see Lp space
.
The set of vectors in Rn+1 whose Euclidean norm is a given positive constant forms an n-sphere.
is the absolute value (also called the modulus) of it, if the complex plane
is identified with the Euclidean plane R2. This identification of the complex number x + iy as a vector in the Euclidean plane, makes the quantity
(as first suggested by Euler) the Euclidean norm associated with the complex number.
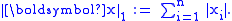
The name relates to the distance a taxi has to drive in a rectangular street grid to get from the origin to the point x.
The set of vectors whose 1-norm is a given constant forms the surface of a cross polytope of dimension equivalent to that of the norm minus 1. The Taxicab norm is also called the L1 norm. The distance derived from this norm is called the Manhattan distance or L1 distance.
The one norm is simply the maximum column sum of absolute values.
In contrast,
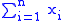
is not a norm because it may yield negative results.
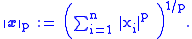
Note that for p = 1 we get the taxicab norm, for p = 2 we get the Euclidean norm, and as p approaches
the p-norm approaches the infinity norm or maximum norm.
This definition is still of some interest for 0 < p < 1, but the resulting function does not define a norm, because it violates the triangle inequality. What is true, even in the measurable analog, is that the corresponding Lp class is a vector space, and it is also true that the function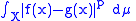
(without p-th root) defines a distance that makes Lp(X) into a complete metric topological vector space
. These spaces are of great interest in functional analysis
, probability theory
, and harmonic analysis
.
However, outside trivial cases, this topological vector space is not locally convex and has no continuous nonzero linear forms. Thus the topological dual space contains only the zero functional.
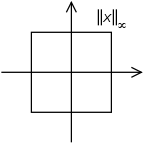
The set of vectors whose infinity norm is a given constant, c, forms the surface of a hypercube
with edge length 2c.
The infinity norm is simply the maximum row sum of absolute values.
of sequences with F–norm
, which is discussed by Stefan Rolewicz in Metric Linear Spaces.
, which is important in coding
and information theory
. In the field of real or complex numbers, the distance of the discrete metric from zero is not homogeneous in the non-zero point; indeed, the distance from zero remains one as its non-zero argument approaches zero. However, the discrete distance of a number from zero does satisfy the other properties of a norm, namely the triangle inequality and positive definiteness. When applied component-wise to vectors, the discrete distance from zero behaves like a non-homogeneous "norm", which counts the number of non-zero components in its vector argument; again, this non-homogeneous "norm" is discontinuous.
In signal processing
and statistics
, David Donoho referred to the zero "norm" with quotation marks. Following Donoho's notation, the zero "norm" of x is simply the number of non-zero elements of x, or the Hamming distance of the vector from zero. When this "norm" is localized to a bounded set, it is the limit of p-norms as p approaches 0. Of course, the zero "norm" is not a B-norm, because it is not positive homogeneous. It is not even an F-norm, because it is discontinuous, jointly and severally, with respect to the scalar argument in scalar-vector multiplication and with respect to its vector argument. Abusing terminology, some engineers omit Donoho's quotation marks and inappropriately call the number-of-nonzeros function the L0 norm (sic.), also misusing the notation for the Lebesgue space of measurable function
s.
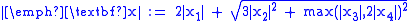
is a norm on R4.
For any norm and any injective linear transformation
A we can define a new norm of x, equal to
In 2D, with A a rotation by 45° and a suitable scaling, this changes the taxicab norm into the maximum norm. In 2D, each A applied to the taxicab norm, up to inversion and interchanging of axes, gives a different unit ball: a parallelogram
of a particular shape, size and orientation. In 3D this is similar but different for the 1-norm (octahedron
s) and the maximum norm (prism
s with parallelogram base).
All the above formulas also yield norms on Cn without modification.
s, with norms
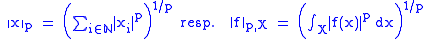
(for complex-valued sequences x resp. functions f defined on
), which can be further generalized (see Haar measure
).
Any inner product induces in a natural way the norm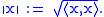
Other examples of infinite dimensional normed vector spaces can be found in the Banach space
article.
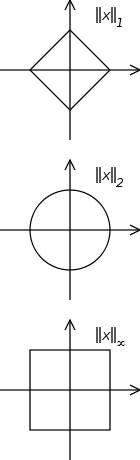The concept of unit circle
(the set of all vectors of norm 1) is different in different norms: for the 1-norm the unit circle in R2 is a square
, for the 2-norm (Euclidean norm) it is the well-known unit circle
, while for the infinity norm it is a different square. For any p-norm it is a superellipse
(with congruent axes). See the accompanying illustration. Note that due to the definition of the norm, the unit circle is always convex
and centrally symmetric (therefore, for example, the unit ball may be a rectangle but cannot be a triangle).
In terms of the vector space, the seminorm defines a topology
on the space, and this is a Hausdorff
topology precisely when the seminorm can distinguish between distinct vectors, which is again equivalent to the seminorm being a norm. The topology thus defined (by either a norm or a seminorm) can be understood either in terms of sequences or open sets. A sequence
of vectors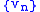
is said to converge
in norm to
if 
as 
. Equivalently, the topology consists of all sets that can be represented as a union of open balls
.
Two norms ||•||α and ||•||β on a vector space V are called equivalent if there exist positive real numbers C and D such that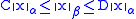
for all x in V. For instance, on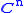
, if p > r > 0, then
In particular,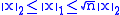
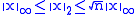
If the vector space is a finite-dimensional real/complex one, all norms are equivalent.
If not, some norms are not.
Equivalent norms define the same notions of continuity and convergence and for many purposes do not need to be distinguished. To be more precise the uniform structure defined by equivalent norms on the vector space is uniformly isomorphic.
Every (semi)-norm is a sublinear function, which implies that every norm is a convex function
. As a result, finding a global optimum of a norm-based objective function is often tractable.
Given a finite family of seminorms pi on a vector space the sum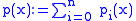
is again a seminorm.
For any norm p on a vector space V, we have that for all u and v ∈ V:
For the lp
norms, we have the Hölder's inequality
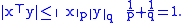
A special case of the above property is the Cauchy–Schwarz inequality
:
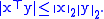
s in V. To each such set, A, corresponds a seminorm pA called the gauge
of A, defined as
with the property that
Conversely:
Any locally convex topological vector space
has a local basis consisting of absolutely convex sets. A common method to construct such a basis is to use a separating family (p) of seminorms p: the collection of all finite intersections of sets {p<1/n} turns the space into a locally convex topological vector space
so that every p is continuous
.
A such method is used to design weak and weak* topologies
.
norm case:
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a norm is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that assigns a strictly positive length or size to all vectors in a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, other than the zero vector. A seminorm, on the other hand, is allowed to assign zero length to some non-zero vectors.
A simple example is the 2-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
R2 equipped with the Euclidean norm. Elements in this vector space (e.g., (3, 7)) are usually drawn as arrows in a 2-dimensional cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
starting at the origin (0, 0). The Euclidean norm assigns to each vector the length of its arrow. Because of this, the Euclidean norm is often known as the magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
.
A vector space with a norm is called a normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
. Similarly, a vector space with a seminorm is called a seminormed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
.
Definition
Given a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V over a subfield
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F of the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s a norm on V is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
with the following properties:
For all a ∈ F and all u, v ∈ V,
- p(av) = |a| p(v), (positive homogeneity or positive scalability).
- p(u + v) ≤ p(u) + p(v) (triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
or subadditivitySubadditive functionIn mathematics, subadditivity is a property of a function that states, roughly, that evaluating the function for the sum of two elements of the domain always returns something less than or equal to the sum of the function's values at each element. There are numerous examples of subadditive...
). - If p(v) = 0 then v is the zero vector (separates points).
A simple consequence of the first two axioms, positive homogeneity and the triangle inequality, is p(0) = 0 and thus
- p(v) ≥ 0 (positivity).
A seminorm is a norm with the 3rd property (separating points) removed.
Although every vector space is seminormed (e.g., with the trivial seminorm in the Examples section below), it may not be normed. Every vector space V with seminorm p(v) induces a normed space V/W, called the quotient space
Quotient space (linear algebra)
In linear algebra, the quotient of a vector space V by a subspace N is a vector space obtained by "collapsing" N to zero. The space obtained is called a quotient space and is denoted V/N ....
, where W is the subspace of V consisting of all vectors v in V with p(v) = 0. The induced norm on V/W is clearly well-defined and is given by:
- p(W + v) = p(v).
A topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
is called normable (seminormable) if the topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of the space can be induced by a norm (seminorm).
The norm of a vector v is usually denoted ||v||, and sometimes |v|. However, the latter notation is generally discouraged, because it is also used to denote the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of scalars and the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of matrices.
Examples
- All norms are seminorms.
- The trivial seminorm, with p(x) = 0 for all x in V.
- The absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
is a norm on the real numbers. - Every linear form f on a vector space defines a seminorm by x → |f(x)|.
Euclidean norm
On an n-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn, the intuitive notion of length of the vector x = (x1, x2, ..., xn) is captured by the formula
This gives the ordinary distance from the origin to the point x, a consequence of the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
.
The Euclidean norm is by far the most commonly used norm on Rn, but there are other norms on this vector space as will be shown below. However all these norms are equivalent in the sense that they all define the same topology.
On an n-dimensional complex space
Complex space
In mathematics, n-dimensional complex space is a multi-dimensional generalisation of the complex numbers, which have both real and imaginary parts or dimensions...
Cn the most common norm is
In both cases we can also express the norm as the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of the inner product of the vector and itself:
where x is represented as a column vector ([x1; x2; ...; xn]), and x* denotes its conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
.
This formula is valid for any inner product space
Inner product space
In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, including Euclidean and complex spaces. For Euclidean spaces, the inner product is equivalent to the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
. Hence, in this specific case the formula can be also written with the following notation:
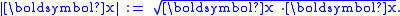
The Euclidean norm is also called the Euclidean length, L2 distance, ℓ2 distance, L2 norm, or ℓ2 norm; see Lp space
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
.
The set of vectors in Rn+1 whose Euclidean norm is a given positive constant forms an n-sphere.
Euclidean norm of a complex number
The Euclidean norm of a complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
is the absolute value (also called the modulus) of it, if the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
is identified with the Euclidean plane R2. This identification of the complex number x + iy as a vector in the Euclidean plane, makes the quantity
(as first suggested by Euler) the Euclidean norm associated with the complex number.Taxicab norm or Manhattan norm
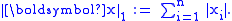
The name relates to the distance a taxi has to drive in a rectangular street grid to get from the origin to the point x.
The set of vectors whose 1-norm is a given constant forms the surface of a cross polytope of dimension equivalent to that of the norm minus 1. The Taxicab norm is also called the L1 norm. The distance derived from this norm is called the Manhattan distance or L1 distance.
The one norm is simply the maximum column sum of absolute values.
In contrast,
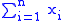
is not a norm because it may yield negative results.
p-norm
Let p ≥ 1 be a real number.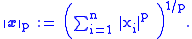Note that for p = 1 we get the taxicab norm, for p = 2 we get the Euclidean norm, and as p approaches
the p-norm approaches the infinity norm or maximum norm.This definition is still of some interest for 0 < p < 1, but the resulting function does not define a norm, because it violates the triangle inequality. What is true, even in the measurable analog, is that the corresponding Lp class is a vector space, and it is also true that the function
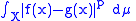
(without p-th root) defines a distance that makes Lp(X) into a complete metric topological vector space
Topological vector space
In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
. These spaces are of great interest in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
, probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, and harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
.
However, outside trivial cases, this topological vector space is not locally convex and has no continuous nonzero linear forms. Thus the topological dual space contains only the zero functional.
Maximum norm (special case of: infinity norm, uniform norm, or supremum norm)
The set of vectors whose infinity norm is a given constant, c, forms the surface of a hypercube
Hypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
with edge length 2c.
The infinity norm is simply the maximum row sum of absolute values.
Zero norm
In probability and functional analysis, the zero norm induces a complete metric topology for the space of measureable functions and for the F-spaceF-space
In functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
of sequences with F–norm
F-space
In functional analysis, an F-space is a vector space V over the real or complex numbers together with a metric d : V × V → R so that...
, which is discussed by Stefan Rolewicz in Metric Linear Spaces.Hamming distance of a vector from zero
In metric geometry, the discrete metric takes the value one for distinct points and zero otherwise. When applied coordinate-wise to the elements of a vector space, the discrete distance defines the Hamming distanceHamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
, which is important in coding
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
and information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
. In the field of real or complex numbers, the distance of the discrete metric from zero is not homogeneous in the non-zero point; indeed, the distance from zero remains one as its non-zero argument approaches zero. However, the discrete distance of a number from zero does satisfy the other properties of a norm, namely the triangle inequality and positive definiteness. When applied component-wise to vectors, the discrete distance from zero behaves like a non-homogeneous "norm", which counts the number of non-zero components in its vector argument; again, this non-homogeneous "norm" is discontinuous.
In signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, David Donoho referred to the zero "norm" with quotation marks. Following Donoho's notation, the zero "norm" of x is simply the number of non-zero elements of x, or the Hamming distance of the vector from zero. When this "norm" is localized to a bounded set, it is the limit of p-norms as p approaches 0. Of course, the zero "norm" is not a B-norm, because it is not positive homogeneous. It is not even an F-norm, because it is discontinuous, jointly and severally, with respect to the scalar argument in scalar-vector multiplication and with respect to its vector argument. Abusing terminology, some engineers omit Donoho's quotation marks and inappropriately call the number-of-nonzeros function the L0 norm (sic.), also misusing the notation for the Lebesgue space of measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
s.
Other norms
Other norms on Rn can be constructed by combining the above; for example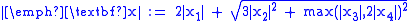is a norm on R4.
For any norm and any injective linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
A we can define a new norm of x, equal to
In 2D, with A a rotation by 45° and a suitable scaling, this changes the taxicab norm into the maximum norm. In 2D, each A applied to the taxicab norm, up to inversion and interchanging of axes, gives a different unit ball: a parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
of a particular shape, size and orientation. In 3D this is similar but different for the 1-norm (octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
s) and the maximum norm (prism
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
s with parallelogram base).
All the above formulas also yield norms on Cn without modification.
Infinite-dimensional case
The generalization of the above norms to an infinite number of components leads to the Lp spaceLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
s, with norms
(for complex-valued sequences x resp. functions f defined on
), which can be further generalized (see Haar measureHaar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
).
Any inner product induces in a natural way the norm
Other examples of infinite dimensional normed vector spaces can be found in the Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
article.
Properties
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
(the set of all vectors of norm 1) is different in different norms: for the 1-norm the unit circle in R2 is a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, for the 2-norm (Euclidean norm) it is the well-known unit circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, while for the infinity norm it is a different square. For any p-norm it is a superellipse
Superellipse
A superellipse is a geometric figure defined in the Cartesian coordinate system as the set of all points withwhere n, a and b are positive numbers....
(with congruent axes). See the accompanying illustration. Note that due to the definition of the norm, the unit circle is always convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
and centrally symmetric (therefore, for example, the unit ball may be a rectangle but cannot be a triangle).
In terms of the vector space, the seminorm defines a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on the space, and this is a Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
topology precisely when the seminorm can distinguish between distinct vectors, which is again equivalent to the seminorm being a norm. The topology thus defined (by either a norm or a seminorm) can be understood either in terms of sequences or open sets. A sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of vectors
is said to convergeModes of convergence
In mathematics, there are many senses in which a sequence or a series is said to be convergent. This article describes various modes of convergence in the settings where they are defined...
in norm to
if as . Equivalently, the topology consists of all sets that can be represented as a union of open ballsBall (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
.
Two norms ||•||α and ||•||β on a vector space V are called equivalent if there exist positive real numbers C and D such that
for all x in V. For instance, on
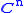, if p > r > 0, thenIn particular,
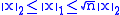
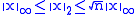
If the vector space is a finite-dimensional real/complex one, all norms are equivalent.
If not, some norms are not.
Equivalent norms define the same notions of continuity and convergence and for many purposes do not need to be distinguished. To be more precise the uniform structure defined by equivalent norms on the vector space is uniformly isomorphic.
Every (semi)-norm is a sublinear function, which implies that every norm is a convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
. As a result, finding a global optimum of a norm-based objective function is often tractable.
Given a finite family of seminorms pi on a vector space the sum
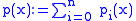
is again a seminorm.
For any norm p on a vector space V, we have that for all u and v ∈ V:
- p(u ± v) ≥ | p(u) − p(v) |
For the lp
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
norms, we have the Hölder's inequality
Hölder's inequality
In mathematical analysis Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces....
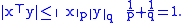
A special case of the above property is the Cauchy–Schwarz inequality
Cauchy–Schwarz inequality
In mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
:
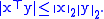
Classification of seminorms: Absolutely convex absorbing sets
All seminorms on a vector space V can be classified in terms of absolutely convex absorbing setAbsorbing set
In functional analysis and related areas of mathematics an absorbing set in a vector space is a set S which can be inflated to include any element of the vector space...
s in V. To each such set, A, corresponds a seminorm pA called the gauge
Minkowski functional
In functional analysis, given a linear space X, a Minkowski functional is a device that uses the linear structure to introduce a topology on X.-Example 1:...
of A, defined as
- pA(x) := infInfimumIn mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
{α : α > 0, x ∈ α A}
with the property that
- {x : pA(x) < 1} ⊆ A ⊆ {x : pA(x) ≤ 1}.
Conversely:
Any locally convex topological vector space
Locally convex topological vector space
In functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
has a local basis consisting of absolutely convex sets. A common method to construct such a basis is to use a separating family (p) of seminorms p: the collection of all finite intersections of sets {p<1/n} turns the space into a locally convex topological vector space
Locally convex topological vector space
In functional analysis and related areas of mathematics, locally convex topological vector spaces or locally convex spaces are examples of topological vector spaces which generalize normed spaces. They can be defined as topological vector spaces whose topology is generated by translations of ...
so that every p is continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
.
A such method is used to design weak and weak* topologies
Weak topology
In mathematics, weak topology is an alternative term for initial topology. The term is most commonly used for the initial topology of a topological vector space with respect to its continuous dual...
.
norm case:
- Suppose now that (p) contains a single p: since (p) is separating, p is a norm, and A={p<1} is its open unit ball. Then A is an absolutely convex bounded neighbourhood of 0, and is continuous.
- The converse is due to Kolmogorov: any locally convex and locally bounded topological vector space is normable. Precisely:
- If V is an absolutely convex bounded neighbourhood of 0, the gauge gV (so that V={gV <1}) is a norm.
See also
- Asymmetric normAsymmetric normIn mathematics, an asymmetric norm on a vector space is a generalization of the concept of a norm.-Definition:Let X be a real vector space...
, a generalization of a norm for which ||x|| and ||−x|| are not necessarily equal. - Matrix norm
- Mahalanobis distanceMahalanobis distanceIn statistics, Mahalanobis distance is a distance measure introduced by P. C. Mahalanobis in 1936. It is based on correlations between variables by which different patterns can be identified and analyzed. It gauges similarity of an unknown sample set to a known one. It differs from Euclidean...
- Manhattan distance
- Relation of norms and metrics, a translation invariant and homogeneous metric can be used to define a norm.
- Normed vector spaceNormed vector spaceIn mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
- One-formOne-formIn linear algebra, a one-form on a vector space is the same as a linear functional on the space. The usage of one-form in this context usually distinguishes the one-forms from higher-degree multilinear functionals on the space. For details, see linear functional.In differential geometry, a...