Continuous function
Encyclopedia
In mathematics
, a continuous function is a function
for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function
is called "bicontinuous".
Continuity of functions is one of the core concepts of topology
, which is treated in full generality below. The introductory portion of this article focuses on the special case where the inputs and outputs of functions are real number
s. In addition, this article discusses the definition for the more general case of functions between two metric space
s. In order theory
, especially in domain theory
, one considers a notion of continuity known as Scott continuity
. Other forms of continuity do exist but they are not discussed in this article.
As an example, consider the function h(t), which describes the height
of a growing flower at time t. This function is continuous. In fact, a dictum of classical physics
states that in nature everything is continuous. By contrast, if M(t) denotes the amount of money in a bank account at time t, then the function jumps whenever money is deposited or withdrawn, so the function M(t) is discontinuous.
in 1817. Preliminary forms of a related definition of the limit were given by Cauchy. Cauchy defined continuity of f as follows: an infinitely small increment of the dependent variable x produces always an infinitely small increment change of f(x). Cauchy in turn defined infinitely small quantities in terms of limits, and his definition parallels the definition used today. The formal definition and the distinction between pointwise continuity and uniform continuity
were first given by Karl Weierstrass
.
from the set of real number
s to the real numbers can be represented by a graph
in the Cartesian plane
; the function is continuous if, roughly speaking, the graph is a single unbroken curve
with no "holes" or "jumps".
There are several ways to make this intuition mathematically rigorous. These definitions are equivalent to one another, so the most convenient definition can be used to determine whether a given function is continuous or not. In the definitions below,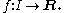
is a function defined on a subset
I of the set R of real numbers. This subset I is referred to as the domain
of f. Possible choices include I=R, the whole set of real numbers, an open interval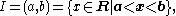
or a closed interval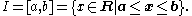
Here, a and b are real numbers.
c of its domain if the limit
of f(x) as x approaches c through domain of f exists and is equal to f(c). In mathematical notation, this is written as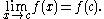
In detail this means three conditions: first, f has to be defined at c. Second, the limit on the left hand side of that equation has to exist. Third, the value of this limit must equal f(c).
The function f is said to be continuous if it is continuous at every point of its domain.
If the point c in the domain of f is not a limit point
of the domain, then this condition is vacuously true
, since x cannot approach c through values not equal c. Thus, for example, every function whose domain is the set of all integers is continuous.
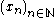of points in the domain which converges to c, the corresponding sequence 
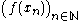converges to f(c). In mathematical notation,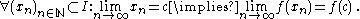 
Given a function f as above and an element c of the domain I, ƒ is said to be continuous at the point c if the following holds: For any number ε > 0, however small, there exists some number δ > 0 such that for all x in the domain of ƒ with c − δ < x < c + δ, the value of ƒ(x) satisfies
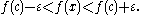
Alternatively written, continuity of ƒ : I → D at c ∈ I means that for every ε > 0 there exists a δ > 0 such that for all x ∈ I,:
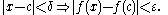
More intuitively, we can say that if we want to get all the ƒ(x) values to stay in some small neighborhood around ƒ(c), we simply need to choose a small enough neighborhood for the x values around c, and we can do that no matter how small the ƒ(x) neighborhood is; ƒ is then continuous at c.
In modern terms, this is generalized by the definition of continuity of a function with respect to a basis for the topology, here the metric topology.
Continuity can also be defined in terms of oscillation
: a function ƒ is continuous at a point x0 if and only if the oscillation is zero; in symbols,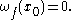
A benefit of this definition is that it quantifies discontinuity: the oscillation gives how much the function is discontinuous at a point.
This definition is useful in descriptive set theory
to study the set of discontinuities and continuous points – the continuous points are the intersection of the sets where the oscillation is less than ε (hence a Gδ set
) – and gives a very quick proof of one direction of the Lebesgue integrability condition.
The oscillation is equivalent to the ε-δ definition by a simple re-arrangement, and by using a limit (lim sup, lim inf) to define oscillation: if (at a given point) for a given ε0 there is no δ that satisfies the ε-δ definition, then the oscillation is at least ε0, and conversely if for every ε there is a desired δ, the oscillation is 0. The oscillation definition can be naturally generalized to maps from a topological space to a metric space.
change in the independent variable corresponds to an infinitesimal change of the dependent variable (see Cours d'analyse, page 34). Non-standard analysis
is a way of making this mathematically rigorous. The real line is augmented by the addition of infinite and infinitesimal numbers to form the hyperreal numbers. In nonstandard analysis, continuity can be defined as follows.
In other words, an infinitesimal increment of the independent variable corresponds to an infinitesimal change of the dependent variable, giving a modern expression to Augustin-Louis Cauchy's definition of continuity.
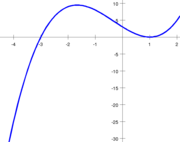All polynomial function
s, such as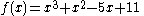
(pictured) are continuous. This is a consequence of the fact that, given two continuous functions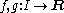
defined on the same domain I, then the sum f + g, and the product fg of the two functions are continuous (on the same domain I). Moreover, the function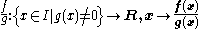
is continuous. (The points where g(x) is zero have to be discarded for f/g to be defined.) For example, the function (pictured)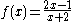
is defined for all real numbers and is continuous at every such point. The question of continuity at does not arise, since is not in the domain of f. There is no continuous function F: R → R that agrees with f(x) for all . The function g(x) = (sin x)/x, defined for all x≠0 is continuous at these points. However, this function can be extended to a continuous function on all real numbers, namely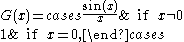
since the limit of g(x), when x approaches 0, is 1. Therefore, the point x=0 is called a removable singularity of g.
Given two continuous functions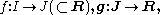
the composition
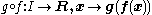
is continuous.
or sign function
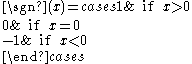
is discontinuous at x=0 but continuous everywhere else. Yet another example: the function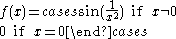
is continuous everywhere apart from x = 0.
Thomae's function,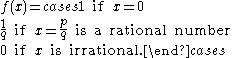
is continuous at all irrational numbers and discontinuous at all rational numbers. In a similar vein, Dirichlet's function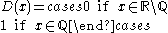
is nowhere continuous.
is an existence theorem
, based on the real number property of completeness, and states:
For example, if a child grows from 1 m to 1.5 m between the ages of two and six years, then, at some time between two and six years of age, the child's height must have been 1.25 m.
As a consequence, if f is continuous on [a, b] and f(a) and f(b) differ in sign
, then, at some point c in [a, b], f(c) must equal zero
.
states that if a function f is defined on a closed interval [a,b] (or any closed and bounded set) and is continuous there, then the function attains its maximum, i.e. there exists c ∈ [a,b] with f(c) ≥ f(x) for all x ∈ [a,b]. The same is true of the minimum of f. These statements are not, in general, true if the function is defined on an open interval (a,b) (or any set that is not both closed and bounded), as, for example, the continuous function f(x) = 1/x, defined on the open interval (0,1), does not attain a maximum, being unbounded above.
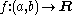
is continuous, as can be shown. The converse does not hold: for example, the absolute value
function
is everywhere continuous. However, it is not differentiable at x = 0 (but is so everywhere else). Weierstrass's function
is everywhere continuous but nowhere differentiable.
The derivative
f' (x) of a differentiable function f(x) need not be continuous. If f' (x) is continuous, f(x) is said to be continuously differentiable. The set of such functions is denoted C1((a, b)). More generally, the set of functions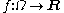
(from an open interval (or open subset of R) Ω to the reals) such that f is n times differentiable and such that the n-th derivative of f is continuous is denoted Cn(Ω). See differentiability class. In the field of computer graphics, these three levels are sometimes called G0 (continuity of position), G1 (continuity of tangency), and G2 (continuity of curvature).
Every continuous function
is integrable (for example in the sense of the Riemann integral
). The converse does not hold, as the (integrable, but discontinuous) sign function
shows.
of functions such that the limit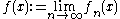
exists for all x in I, the resulting function f(x) is referred to as the pointwise limit
of the sequence of functions (fn)n∈N. The pointwise limit function need not be continuous, even if all functions fn are continuous, as the animation at the right shows. However, f is continuous when the sequence converges uniformly, by the uniform convergence theorem. This theorem can be used to show that the exponential function
s, logarithm
s, square root
function, trigonometric function
s are continuous.
. Roughly speaking, a function is right-continuous if no jump occurs when the limit point is approached from the right. More formally, ƒ is said to be right-continuous at the point c if the following holds: For any number ε > 0 however small, there exists some number δ > 0 such that for all x in the domain with , the value of ƒ(x) will satisfy
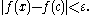
This is the same condition as for continuous functions, except that it is required to hold for x strictly larger than c only. Requiring it instead for all x with yields the notion of left-continuous functions. A function is continuous if and only if it is both right-continuous and left-continuous.
A function f is upper semi-continuous if, roughly, any jumps that might occur only go up, but not down. That is, for any ε > 0, there exists some number δ > 0 such that for all x in the domain with |x − c| < δ, the value of ƒ(x) satisfies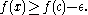
s. A metric space is a set X equipped with a function (called metric
) dX, that can be thought of as a measurement of the distance of any two elements in X. Formally, the metric is a function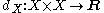
that satisfies a number of requirements, notably the triangle inequality
. Given two metric spaces (X, dX) and (Y, dY) and a function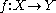
then f is continuous at the point c in X (with respect to the given metrics) if for any positive real number ε, there exists a positive real number δ such that all x in X satisfying dX(x, c) < δ will also satisfy dY(f(x), f(c)) < ε. As in the case of real functions above, this is equivalent to the condition that for every sequence (xn) in X with limit lim xn = c, we have lim f(xn) = f(c). The latter condition can be weakened as follows: f is continuous at the point c if and only if for every convergent sequence (xn) in X with limit c, the sequence (f(xn)) is a Cauchy sequence
, and c is in the domain of f.
The set of points at which a function between metric spaces is continuous is a Gδ set – this follows from the ε-δ definition of continuity.
This notion of continuity is applied, for example, in functional analysis
. A key statement in this area says that a linear operator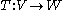
between normed vector space
s V and W (which are vector spaces equipped with a compatible norm
, denoted ||x||)
is continuous if and only if it is bounded, that is, there is a constant K such that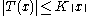
for all x in V.
The concept of continuity for functions between metric spaces can be strengthened in various ways by limiting the way δ depends on ε and c in the definition above. Intuitively, a function f as above is uniformly continuous if the δ does
not depend on the point c. More precisely, it is required that for every real number
ε > 0 there exists δ > 0 such that for every c, b ∈ X with dX(b, c) < δ, we have that dY(f(b), f(c)) < ε. Thus, any uniformly continuous function is continuous. The converse does not hold in general, but holds when the domain space X is compact. Uniformly continuous maps can be defined in the more general situation of uniform space
s.
A function is Hölder continuous with exponent α (a real number) if there is a constant K such that for all b and c in X, the inequality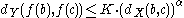
holds. Any Hölder continuous function is uniformly continuous. The particular case is referred to as Lipschitz continuity
. That is, a function is Lipschitz continuous if there is a constant K such that the inequality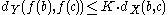
holds any b, c in X. The Lipschitz condition occurs, for example, in the Picard–Lindelöf theorem
concerning the solutions of ordinary differential equation
s.
Yet another, more abstract notion of continuity is continuity of functions between topological space
s. A topological space is a set X together with a set of subset
s of X. These subsets are called open subsets. Intuitively, points belonging to some open subset are close to one another; however there is no formal notion of distance, as in the case of metric spaces. The set of open subsets needs to satisfy a few requirements in order to qualify for a topological space. If they are satisfied, this set of subsets is called a topology
on the set X.
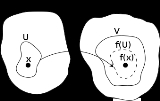
A function
between two topological spaces X and Y is continuous if for every open set V ⊆ Y, the inverse image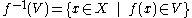
is an open subset of X. That is, f is a function between the sets X and Y (not on the elements of the topology TX), but the continuity of f depend on the topologies used on X and Y.
This is equivalent to the condition that the preimages of the closed set
s (which are the complements of the open subsets) in Y are closed in X.
An extreme example: if a set X is given the discrete topology (in which every subset is open), all functions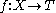
to any topological space T are continuous. On the other hand, if X is equipped with the indiscrete topology (in which the only open subsets are the empty set and X) and the space T set is at least T0, then the only continuous functions are the constant functions. Conversely, any function whose range is indiscrete is continuous.
exist and thus there are several equivalent ways to define a continuous function.
If X and Y are metric spaces, it is equivalent to consider the neighborhood system of open balls centered at x and f(x) instead of all neighborhoods. This gives back the above δ-ε definition of continuity in the context of metric spaces. However, in general topological spaces, there is no notion of nearness or distance.
Note, however, that if the target space is Hausdorff
, it is still true that f is continuous at a if and only if the limit of f as x approaches a is f(a). At an isolated point, every function is continuous.
, but for some spaces that are too large in some sense, one specifies also when a point is the limit of more general sets of points indexed by a directed set
, known as nets
. A function is continuous only if it takes limits of sequences to limits of sequences. In the former case, preservation of limits is also sufficient; in the latter, a function may preserve all limits of sequences yet still fail to be continuous, and preservation of nets is a necessary and sufficient condition.
In detail, a function f : X → Y is sequentially continuous if whenever a sequence (xn) in X converges to a limit x, the sequence (f(xn)) converges to f(x). Thus sequentially continuous functions "preserve sequential limits". Every continuous function is sequentially continuous. If X is a first-countable space
and countable choice
holds, then the converse also holds: any function preserving sequential limits is continuous. In particular, if X is a metric space, sequential continuity and continuity are equivalent. For non first-countable spaces, sequential continuity might be strictly weaker than continuity. (The spaces for which the two properties are equivalent are called sequential space
s.) This motivates the consideration of nets instead of sequences in general topological spaces. Continuous functions preserve limits of nets, and in fact this property characterizes continuous functions.
s (denoted cl) which assigns to any subset A ⊆ X its closure
or interior operators (denoted int), which assigns to any subset A of X its interior
. In these terms, a function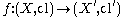
between topological spaces is continuous in the sense above if and only if for all subsets A of X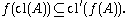
That is to say, given any element x of X that is in the closure of any subset A, f(x) belongs to the closure of f(A). This is equivalent to the requirement that for all subsets A' of X'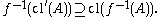 
Moreover,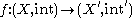
is continuous if and only if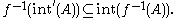
for any subset A of X.
The possible topologies on a fixed set X are partially ordered: a topology τ1 is said to be coarser
than another topology τ2 (notation: τ1 ⊆ τ2) if every open subset with respect to τ1 is also open with respect to τ2. Then, the identity map
is continuous if and only if τ1 ⊆ τ2 (see also comparison of topologies
). More generally, a continuous function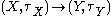
stays continuous if the topology τX is replaced by a weaker topology and/or τY is replaced by a stronger topology.
, that inverse is continuous, and if a continuous map g has an inverse, that inverse is open. Given a bijective function f between two topological spaces, the inverse function f−1 need not be continuous. A bijective continuous function with continuous inverse function is called a homeomorphism
.
If a continuous bijection has as its domain a compact space
and its codomain is Hausdorff
, then it is a homeomorphism, as can be shown.
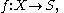
where X is a topological space and S is a set (without a specified topology), the final topology
on S is defined by letting the open sets of S be those subsets A of S for which f−1(A) is open in X. If S has an existing topology, f is continuous with respect to this topology if and only if the existing topology is coarser
than the final topology on S. Thus the final topology can be characterized as the finest topology on S that makes f continuous. If f is surjective, this topology is canonically identified with the quotient topology under the equivalence relation
defined by f.
Dually, for a function f from a set S to a topological space, the initial topology
on S has as open subsets A of S those subsets for which f(A) is open in X. If S has an existing topology, f is continuous with respect to this topology if and only if the existing topology is finer than the initial topology on S. Thus the initial topology can be characterized as the coarsest topology on S that makes f continuous. If f is injective, this topology is canonically identified with the subspace topology
of S, viewed as a subset of X.
More generally, given a set S, specifying the set of continuous functions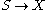
into all topological spaces X defines a topology. Dually
, a similar idea can be applied to maps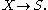
This is an instance of a universal property
.
, an order-preserving function f : X → Y between two complete lattice
s X and Y (particular types of partially ordered set
s) is continuous
if for each subset A of X, we have sup(f(A)) = f(sup(A)). Here sup is the supremum
with respect to the orderings in X and Y, respectively. Applying this to the complete lattice consisting of the open subsets of a topological space, this gives back the notion of continuity for maps between topological spaces.
In category theory
, a functor
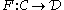
between two categories
is called continuous, if it commutes with small limits
. That is to say,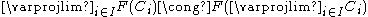
for any small (i.e., indexed by a set I, as opposed to a class) diagram of objects in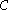
.
A continuity space is a generalization of metric spaces and posets, which uses the concept of quantale
s, and that can be used to unify the notions of metric spaces and domain
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a continuous function is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
is called "bicontinuous".
Continuity of functions is one of the core concepts of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, which is treated in full generality below. The introductory portion of this article focuses on the special case where the inputs and outputs of functions are real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s. In addition, this article discusses the definition for the more general case of functions between two metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s. In order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, especially in domain theory
Domain theory
Domain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
, one considers a notion of continuity known as Scott continuity
Scott continuity
In mathematics, given two partially ordered sets P and Q a function f : P \rightarrow Q between them is Scott-continuous if it preserves all directed suprema, i.e...
. Other forms of continuity do exist but they are not discussed in this article.
As an example, consider the function h(t), which describes the height
Height
Height is the measurement of vertical distance, but has two meanings in common use. It can either indicate how "tall" something is, or how "high up" it is. For example "The height of the building is 50 m" or "The height of the airplane is 10,000 m"...
of a growing flower at time t. This function is continuous. In fact, a dictum of classical physics
Classical physics
What "classical physics" refers to depends on the context. When discussing special relativity, it refers to the Newtonian physics which preceded relativity, i.e. the branches of physics based on principles developed before the rise of relativity and quantum mechanics...
states that in nature everything is continuous. By contrast, if M(t) denotes the amount of money in a bank account at time t, then the function jumps whenever money is deposited or withdrawn, so the function M(t) is discontinuous.
History
A form of this epsilon-delta definition of continuity was first given by Bernard BolzanoBernard Bolzano
Bernhard Placidus Johann Nepomuk Bolzano , Bernard Bolzano in English, was a Bohemian mathematician, logician, philosopher, theologian, Catholic priest and antimilitarist of German mother tongue.-Family:Bolzano was the son of two pious Catholics...
in 1817. Preliminary forms of a related definition of the limit were given by Cauchy. Cauchy defined continuity of f as follows: an infinitely small increment of the dependent variable x produces always an infinitely small increment change of f(x). Cauchy in turn defined infinitely small quantities in terms of limits, and his definition parallels the definition used today. The formal definition and the distinction between pointwise continuity and uniform continuity
Uniform continuity
In mathematics, a function f is uniformly continuous if, roughly speaking, it is possible to guarantee that f and f be as close to each other as we please by requiring only that x and y are sufficiently close to each other; unlike ordinary continuity, the maximum distance between x and y cannot...
were first given by Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
.
Definition
A functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
from the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s to the real numbers can be represented by a graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
in the Cartesian plane
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
; the function is continuous if, roughly speaking, the graph is a single unbroken curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
with no "holes" or "jumps".
There are several ways to make this intuition mathematically rigorous. These definitions are equivalent to one another, so the most convenient definition can be used to determine whether a given function is continuous or not. In the definitions below,
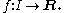
is a function defined on a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
I of the set R of real numbers. This subset I is referred to as the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of f. Possible choices include I=R, the whole set of real numbers, an open interval
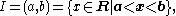
or a closed interval
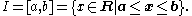
Here, a and b are real numbers.
Definition in terms of limits of functions
The function f is continuous at some pointPoint (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
c of its domain if the limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
of f(x) as x approaches c through domain of f exists and is equal to f(c). In mathematical notation, this is written as
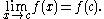
In detail this means three conditions: first, f has to be defined at c. Second, the limit on the left hand side of that equation has to exist. Third, the value of this limit must equal f(c).
The function f is said to be continuous if it is continuous at every point of its domain.
If the point c in the domain of f is not a limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
of the domain, then this condition is vacuously true
Vacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
, since x cannot approach c through values not equal c. Thus, for example, every function whose domain is the set of all integers is continuous.
Definition in terms of limits of sequences
One can instead require that for any sequence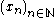 of points in the domain which converges to c, the corresponding sequence 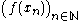converges to f(c). In mathematical notation,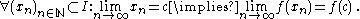 Weierstrass definition (epsilon-delta) of continuous functions
Explicitly including the definition of the limit of a function, we obtain a self-contained definition:Given a function f as above and an element c of the domain I, ƒ is said to be continuous at the point c if the following holds: For any number ε > 0, however small, there exists some number δ > 0 such that for all x in the domain of ƒ with c − δ < x < c + δ, the value of ƒ(x) satisfies
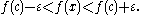
Alternatively written, continuity of ƒ : I → D at c ∈ I means that for every ε > 0 there exists a δ > 0 such that for all x ∈ I,:
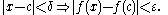
More intuitively, we can say that if we want to get all the ƒ(x) values to stay in some small neighborhood around ƒ(c), we simply need to choose a small enough neighborhood for the x values around c, and we can do that no matter how small the ƒ(x) neighborhood is; ƒ is then continuous at c.
In modern terms, this is generalized by the definition of continuity of a function with respect to a basis for the topology, here the metric topology.
Definition using oscillation
Oscillation (mathematics)
In mathematics, oscillation is the behaviour of a sequence of real numbers or a real-valued function, which does not converge, but also does not diverge to +∞ or −∞; that is, oscillation is the failure to have a limit, and is also a quantitative measure for that.Oscillation is defined as the...
: a function ƒ is continuous at a point x0 if and only if the oscillation is zero; in symbols,
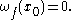A benefit of this definition is that it quantifies discontinuity: the oscillation gives how much the function is discontinuous at a point.This definition is useful in descriptive set theory
Descriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
to study the set of discontinuities and continuous points – the continuous points are the intersection of the sets where the oscillation is less than ε (hence a Gδ set
G-delta set
In the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in Germany with G for Gebiet meaning open set in this case and δ for Durchschnitt .The term inner limiting set is also used...
) – and gives a very quick proof of one direction of the Lebesgue integrability condition.
The oscillation is equivalent to the ε-δ definition by a simple re-arrangement, and by using a limit (lim sup, lim inf) to define oscillation: if (at a given point) for a given ε0 there is no δ that satisfies the ε-δ definition, then the oscillation is at least ε0, and conversely if for every ε there is a desired δ, the oscillation is 0. The oscillation definition can be naturally generalized to maps from a topological space to a metric space.
Definition using the hyperreals
Cauchy defined continuity of a function in the following intuitive terms: an infinitesimalInfinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
change in the independent variable corresponds to an infinitesimal change of the dependent variable (see Cours d'analyse, page 34). Non-standard analysis
Non-standard analysis
Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...
is a way of making this mathematically rigorous. The real line is augmented by the addition of infinite and infinitesimal numbers to form the hyperreal numbers. In nonstandard analysis, continuity can be defined as follows.
- A function ƒ from the reals to the reals is continuous if its natural extension to the hyperreals has the property that for real x and infinitesimal dx, is infinitesimal.
In other words, an infinitesimal increment of the independent variable corresponds to an infinitesimal change of the dependent variable, giving a modern expression to Augustin-Louis Cauchy's definition of continuity.
Examples
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, such as
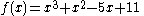
(pictured) are continuous. This is a consequence of the fact that, given two continuous functions
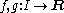
defined on the same domain I, then the sum f + g, and the product fg of the two functions are continuous (on the same domain I). Moreover, the function
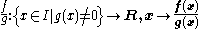
is continuous. (The points where g(x) is zero have to be discarded for f/g to be defined.) For example, the function (pictured)
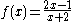
is defined for all real numbers and is continuous at every such point. The question of continuity at does not arise, since is not in the domain of f. There is no continuous function F: R → R that agrees with f(x) for all . The function g(x) = (sin x)/x, defined for all x≠0 is continuous at these points. However, this function can be extended to a continuous function on all real numbers, namely
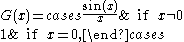
since the limit of g(x), when x approaches 0, is 1. Therefore, the point x=0 is called a removable singularity of g.
Given two continuous functions
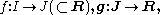
the composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
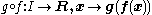
is continuous.
Non-examples
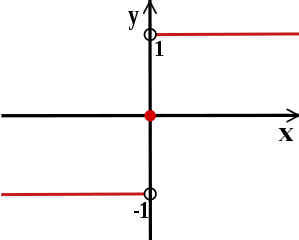
An example of a discontinuous function is the function f defined by f(x) = 1 if x > 0, f(x) = 0 if x ≤ 0. Pick for instance ε = . There is no δ-neighborhood around x = 0 that will force all the f(x) values to be within ε of f(0). Intuitively we can think of this type of discontinuity as a sudden jump in function values. Similarly, the signumSign function
In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
or sign function
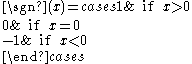
is discontinuous at x=0 but continuous everywhere else. Yet another example: the function
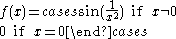
is continuous everywhere apart from x = 0.
Thomae's function,
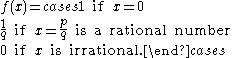
is continuous at all irrational numbers and discontinuous at all rational numbers. In a similar vein, Dirichlet's function
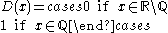
is nowhere continuous.
Intermediate value theorem
The intermediate value theoremIntermediate value theorem
In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....
is an existence theorem
Existence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
, based on the real number property of completeness, and states:
- If the real-valued function f is continuous on the closed intervalInterval (mathematics)In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[a, b] and k is some number between f(a) and f(b), then there is some number c in [a, b] such that f(c) = k.
For example, if a child grows from 1 m to 1.5 m between the ages of two and six years, then, at some time between two and six years of age, the child's height must have been 1.25 m.
As a consequence, if f is continuous on [a, b] and f(a) and f(b) differ in sign
Sign (mathematics)
In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...
, then, at some point c in [a, b], f(c) must equal zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
.
Extreme value theorem
The extreme value theoremExtreme value theorem
In calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
states that if a function f is defined on a closed interval [a,b] (or any closed and bounded set) and is continuous there, then the function attains its maximum, i.e. there exists c ∈ [a,b] with f(c) ≥ f(x) for all x ∈ [a,b]. The same is true of the minimum of f. These statements are not, in general, true if the function is defined on an open interval (a,b) (or any set that is not both closed and bounded), as, for example, the continuous function f(x) = 1/x, defined on the open interval (0,1), does not attain a maximum, being unbounded above.
Relation to differentiability and integrability
Every differentiable functionDifferentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
is continuous, as can be shown. The converse does not hold: for example, the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
function
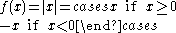
is everywhere continuous. However, it is not differentiable at x = 0 (but is so everywhere else). Weierstrass's function
Weierstrass function
In mathematics, the Weierstrass function is a pathological example of a real-valued function on the real line. The function has the property that it is continuous everywhere but differentiable nowhere...
is everywhere continuous but nowhere differentiable.
The derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
f
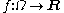
(from an open interval (or open subset of R) Ω to the reals) such that f is n times differentiable and such that the n-th derivative of f is continuous is denoted Cn(Ω). See differentiability class. In the field of computer graphics, these three levels are sometimes called G0 (continuity of position), G1 (continuity of tangency), and G2 (continuity of curvature).
Every continuous function
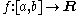
is integrable (for example in the sense of the Riemann integral
Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
). The converse does not hold, as the (integrable, but discontinuous) sign function
Sign function
In mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
shows.
Pointwise and uniform limits
Given a sequenceof functions such that the limit
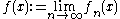
exists for all x in I, the resulting function f(x) is referred to as the pointwise limit
Pointwise convergence
In mathematics, pointwise convergence is one of various senses in which a sequence of functions can converge to a particular function.-Definition:...
of the sequence of functions (fn)n∈N. The pointwise limit function need not be continuous, even if all functions fn are continuous, as the animation at the right shows. However, f is continuous when the sequence converges uniformly, by the uniform convergence theorem. This theorem can be used to show that the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
s, logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
s, square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
function, trigonometric function
Trigonometric function
In mathematics, the trigonometric functions are functions of an angle. They are used to relate the angles of a triangle to the lengths of the sides of a triangle...
s are continuous.
Directional and semi-continuity
Discontinuous functions may be discontinuous in a restricted way, giving rise to the concept of directional continuity (or right and left continuous functions) and semi-continuitySemi-continuity
In mathematical analysis, semi-continuity is a property of extended real-valued functions that is weaker than continuity...
. Roughly speaking, a function is right-continuous if no jump occurs when the limit point is approached from the right. More formally, ƒ is said to be right-continuous at the point c if the following holds: For any number ε > 0 however small, there exists some number δ > 0 such that for all x in the domain with , the value of ƒ(x) will satisfy
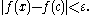
This is the same condition as for continuous functions, except that it is required to hold for x strictly larger than c only. Requiring it instead for all x with yields the notion of left-continuous functions. A function is continuous if and only if it is both right-continuous and left-continuous.
A function f is upper semi-continuous if, roughly, any jumps that might occur only go up, but not down. That is, for any ε > 0, there exists some number δ > 0 such that for all x in the domain with |x − c| < δ, the value of ƒ(x) satisfies
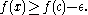
Continuous functions between metric spaces
The concept of continuous real-valued functions can be generalized to functions between metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s. A metric space is a set X equipped with a function (called metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
) dX, that can be thought of as a measurement of the distance of any two elements in X. Formally, the metric is a function
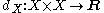
that satisfies a number of requirements, notably the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
. Given two metric spaces (X, dX) and (Y, dY) and a function
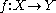
then f is continuous at the point c in X (with respect to the given metrics) if for any positive real number ε, there exists a positive real number δ such that all x in X satisfying dX(x, c) < δ will also satisfy dY(f(x), f(c)) < ε. As in the case of real functions above, this is equivalent to the condition that for every sequence (xn) in X with limit lim xn = c, we have lim f(xn) = f(c). The latter condition can be weakened as follows: f is continuous at the point c if and only if for every convergent sequence (xn) in X with limit c, the sequence (f(xn)) is a Cauchy sequence
Cauchy sequence
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each other as the sequence progresses...
, and c is in the domain of f.
The set of points at which a function between metric spaces is continuous is a Gδ set – this follows from the ε-δ definition of continuity.
This notion of continuity is applied, for example, in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. A key statement in this area says that a linear operator
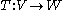
between normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
s V and W (which are vector spaces equipped with a compatible norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
, denoted ||x||)
is continuous if and only if it is bounded, that is, there is a constant K such that
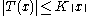
for all x in V.
Uniform, Hölder and Lipschitz continuity
not depend on the point c. More precisely, it is required that for every real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
ε > 0 there exists δ > 0 such that for every c, b ∈ X with dX(b, c) < δ, we have that dY(f(b), f(c)) < ε. Thus, any uniformly continuous function is continuous. The converse does not hold in general, but holds when the domain space X is compact. Uniformly continuous maps can be defined in the more general situation of uniform space
Uniform space
In the mathematical field of topology, a uniform space is a set with a uniform structure. Uniform spaces are topological spaces with additional structure which is used to define uniform properties such as completeness, uniform continuity and uniform convergence.The conceptual difference between...
s.
A function is Hölder continuous with exponent α (a real number) if there is a constant K such that for all b and c in X, the inequality
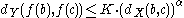
holds. Any Hölder continuous function is uniformly continuous. The particular case is referred to as Lipschitz continuity
Lipschitz continuity
In mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
. That is, a function is Lipschitz continuous if there is a constant K such that the inequality
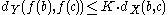
holds any b, c in X. The Lipschitz condition occurs, for example, in the Picard–Lindelöf theorem
Picard–Lindelöf theorem
In mathematics, in the study of differential equations, the Picard–Lindelöf theorem, Picard's existence theorem or Cauchy–Lipschitz theorem is an important theorem on existence and uniqueness of solutions to first-order equations with given initial conditions.The theorem is named after Charles...
concerning the solutions of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s.
Continuous functions between topological spaces
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s. A topological space is a set X together with a set of subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of X. These subsets are called open subsets. Intuitively, points belonging to some open subset are close to one another; however there is no formal notion of distance, as in the case of metric spaces. The set of open subsets needs to satisfy a few requirements in order to qualify for a topological space. If they are satisfied, this set of subsets is called a topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
on the set X.
A function
between two topological spaces X and Y is continuous if for every open set V ⊆ Y, the inverse image
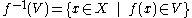
is an open subset of X. That is, f is a function between the sets X and Y (not on the elements of the topology TX), but the continuity of f depend on the topologies used on X and Y.
This is equivalent to the condition that the preimages of the closed set
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
s (which are the complements of the open subsets) in Y are closed in X.
An extreme example: if a set X is given the discrete topology (in which every subset is open), all functions
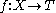
to any topological space T are continuous. On the other hand, if X is equipped with the indiscrete topology (in which the only open subsets are the empty set and X) and the space T set is at least T0, then the only continuous functions are the constant functions. Conversely, any function whose range is indiscrete is continuous.
Alternative definitions
Several equivalent definitions for a topological structureCharacterizations of the category of topological spaces
In mathematics, a topological space is usually defined in terms of open sets. However, there are many equivalent characterizations of the category of topological spaces...
exist and thus there are several equivalent ways to define a continuous function.
Neighborhood definition
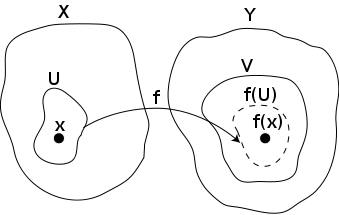
Definitions based on preimages are often difficult to use directly. The following criterion expresses continuity in terms of neighborhoods: f is continuous at some point x ∈ X if and only if for any neighborhood V of f(x), there is a neighborhood U of x such that f(U) ⊆ V. Intuitively, continuity means no matter how "small" V becomes, there is always a U containing x that maps inside V.If X and Y are metric spaces, it is equivalent to consider the neighborhood system of open balls centered at x and f(x) instead of all neighborhoods. This gives back the above δ-ε definition of continuity in the context of metric spaces. However, in general topological spaces, there is no notion of nearness or distance.
Note, however, that if the target space is Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, it is still true that f is continuous at a if and only if the limit of f as x approaches a is f(a). At an isolated point, every function is continuous.
Sequences and nets
In several contexts, the topology of a space is conveniently specified in terms of limit points. In many instances, this is accomplished by specifying when a point is the limit of a sequenceLimit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
, but for some spaces that are too large in some sense, one specifies also when a point is the limit of more general sets of points indexed by a directed set
Directed set
In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
, known as nets
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
. A function is continuous only if it takes limits of sequences to limits of sequences. In the former case, preservation of limits is also sufficient; in the latter, a function may preserve all limits of sequences yet still fail to be continuous, and preservation of nets is a necessary and sufficient condition.
In detail, a function f : X → Y is sequentially continuous if whenever a sequence (xn) in X converges to a limit x, the sequence (f(xn)) converges to f(x). Thus sequentially continuous functions "preserve sequential limits". Every continuous function is sequentially continuous. If X is a first-countable space
First-countable space
In topology, a branch of mathematics, a first-countable space is a topological space satisfying the "first axiom of countability". Specifically, a space X is said to be first-countable if each point has a countable neighbourhood basis...
and countable choice
Axiom of countable choice
The axiom of countable choice or axiom of denumerable choice, denoted ACω, is an axiom of set theory, similar to the axiom of choice. It states that any countable collection of non-empty sets must have a choice function...
holds, then the converse also holds: any function preserving sequential limits is continuous. In particular, if X is a metric space, sequential continuity and continuity are equivalent. For non first-countable spaces, sequential continuity might be strictly weaker than continuity. (The spaces for which the two properties are equivalent are called sequential space
Sequential space
In topology and related fields of mathematics, a sequential space is a topological space that satisfies a very weak axiom of countability. Sequential spaces are the most general class of spaces for which sequences suffice to determine the topology....
s.) This motivates the consideration of nets instead of sequences in general topological spaces. Continuous functions preserve limits of nets, and in fact this property characterizes continuous functions.
Closure operator definition
Instead of specifying the open subsets of a topological space, the topology can also be determined by closure operatorClosure operator
In mathematics, a closure operator on a set S is a function cl: P → P from the power set of S to itself which satisfies the following conditions for all sets X,Y ⊆ S....
s (denoted cl) which assigns to any subset A ⊆ X its closure
Closure
Closure may refer to:* Closure used to seal a bottle, jug, jar, can, or other container** Closure , a stopper* Closure , the process by which an organization ceases operations...
or interior operators (denoted int), which assigns to any subset A of X its interior
Interior
Coastal regions of a territory are often the most densely populated due to their greater economic productivity or colonial history. This leads to a contrast with the interior of the territory, which is sparsely populated...
. In these terms, a function
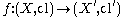
between topological spaces is continuous in the sense above if and only if for all subsets A of X
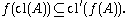
That is to say, given any element x of X that is in the closure of any subset A, f(x) belongs to the closure of f(A). This is equivalent to the requirement that for all subsets A
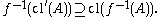
Moreover,
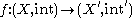
is continuous if and only if
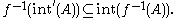
for any subset A of X.
Properties
If f : X → Y and g : Y → Z are continuous, then so is the composition g ∘ f : X → Z. If f : X → Y is continuous and- X is compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
, then f(X) is compact. - X is connectedConnected spaceIn topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
, then f(X) is connected. - X is path-connected, then f(X) is path-connected.
- X is LindelöfLindelöf spaceIn mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
, then f(X) is Lindelöf. - X is separable, then f(X) is separable.
The possible topologies on a fixed set X are partially ordered: a topology τ1 is said to be coarser
Comparison of topologies
In topology and related areas of mathematics comparison of topologies refers to the fact that two topological structures on a given set may stand in relation to each other. The set of all possible topologies on a given set forms a partially ordered set...
than another topology τ2 (notation: τ1 ⊆ τ2) if every open subset with respect to τ1 is also open with respect to τ2. Then, the identity map
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
- idX : (X, τ2) → (X, τ1)
is continuous if and only if τ1 ⊆ τ2 (see also comparison of topologies
Comparison of topologies
In topology and related areas of mathematics comparison of topologies refers to the fact that two topological structures on a given set may stand in relation to each other. The set of all possible topologies on a given set forms a partially ordered set...
). More generally, a continuous function
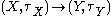
stays continuous if the topology τX is replaced by a weaker topology and/or τY is replaced by a stronger topology.
Homeomorphisms
Symmetric to the concept of a continuous map is an open map, for which images of open sets are open. In fact, if an open map f has an inverse functionInverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
, that inverse is continuous, and if a continuous map g has an inverse, that inverse is open. Given a bijective function f between two topological spaces, the inverse function f−1 need not be continuous. A bijective continuous function with continuous inverse function is called a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
.
If a continuous bijection has as its domain a compact space
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
and its codomain is Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, then it is a homeomorphism, as can be shown.
Defining topologies via continuous functions
Given a function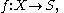where X is a topological space and S is a set (without a specified topology), the final topology
Final topology
In general topology and related areas of mathematics, the final topology on a set X, with respect to a family of functions into X, is the finest topology on X which makes those functions continuous.- Definition :Given a set X and a family of topological spaces Y_i with functionsf_i: Y_i \to Xthe...
on S is defined by letting the open sets of S be those subsets A of S for which f−1(A) is open in X. If S has an existing topology, f is continuous with respect to this topology if and only if the existing topology is coarser
Comparison of topologies
In topology and related areas of mathematics comparison of topologies refers to the fact that two topological structures on a given set may stand in relation to each other. The set of all possible topologies on a given set forms a partially ordered set...
than the final topology on S. Thus the final topology can be characterized as the finest topology on S that makes f continuous. If f is surjective, this topology is canonically identified with the quotient topology under the equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
defined by f.
Dually, for a function f from a set S to a topological space, the initial topology
Initial topology
In general topology and related areas of mathematics, the initial topology on a set X, with respect to a family of functions on X, is the coarsest topology on X which makes those functions continuous.The subspace topology and product topology constructions are both special cases of initial...
on S has as open subsets A of S those subsets for which f(A) is open in X. If S has an existing topology, f is continuous with respect to this topology if and only if the existing topology is finer than the initial topology on S. Thus the initial topology can be characterized as the coarsest topology on S that makes f continuous. If f is injective, this topology is canonically identified with the subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
of S, viewed as a subset of X.
More generally, given a set S, specifying the set of continuous functions
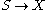
into all topological spaces X defines a topology. Dually
Duality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
, a similar idea can be applied to maps
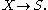
This is an instance of a universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
.
Related notions
Various other mathematical domains use the concept of continuity in different, but related meanings. For example, in order theoryOrder theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, an order-preserving function f : X → Y between two complete lattice
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
s X and Y (particular types of partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s) is continuous
Scott continuity
In mathematics, given two partially ordered sets P and Q a function f : P \rightarrow Q between them is Scott-continuous if it preserves all directed suprema, i.e...
if for each subset A of X, we have sup(f(A)) = f(sup(A)). Here sup is the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
with respect to the orderings in X and Y, respectively. Applying this to the complete lattice consisting of the open subsets of a topological space, this gives back the notion of continuity for maps between topological spaces.
In category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
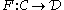
between two categories
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
is called continuous, if it commutes with small limits
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
. That is to say,
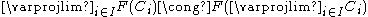
for any small (i.e., indexed by a set I, as opposed to a class) diagram of objects in
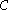.A continuity space is a generalization of metric spaces and posets, which uses the concept of quantale
Quantale
In mathematics, quantales are certain partially ordered algebraic structures that generalize locales as well as various multiplicative lattices of ideals from ring theory and functional analysis...
s, and that can be used to unify the notions of metric spaces and domain
Domain theory
Domain theory is a branch of mathematics that studies special kinds of partially ordered sets commonly called domains. Consequently, domain theory can be considered as a branch of order theory. The field has major applications in computer science, where it is used to specify denotational...
s.