Final topology
Encyclopedia
In general topology
and related areas of mathematics
, the final topology (or strong topology or colimit topology or inductive topology) on a set
, with respect to a family of functions into 
, is the finest topology on X which makes those functions continuous.
and a family of topological space
s
with functions
the final topology
on 
is the finest topology such that each
is continuous.
Explicitly, the final topology may be described as follows: a subset U of X is open if and only if
is open in Yi for each i ∈ I.
is closed/open if and only if
its preimage under fi is closed/open in
for each i ∈ I.
The final topology on X can be characterized by the following universal property
: a function
from 
to some space 
is continuous if and only if 
is continuous for each i ∈ I.
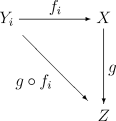By the universal property of the disjoint union topology we know that given any family of continuous maps fi : Yi → X there is a unique continuous map
If the family of maps fi covers X (i.e. each x in X lies in the image of some fi) then the map f will be a quotient map if and only if X has the final topology determined by the maps fi.
, the final topology construction can be described as follows. Let Y be a functor
from a discrete category
J to the category of topological spaces
Top which selects the spaces Yi for i in J. Let Δ be the diagonal functor from Top to the functor category
TopJ (this functor sends each space X to the constant functor to X). The comma category
(Y ↓ Δ) is then the category of cones from Y, i.e. objects in (Y ↓ Δ) are pairs (X, f) where fi : Yi → X is a family of continuous maps to X. If U is the forgetful functor
from Top to Set and Δ′ is the diagonal functor from Set to SetJ then the comma category (UY ↓ Δ′) is the category of all cones from UY. The final topology construction can then be described as a functor from (UY ↓ Δ′) to (Y ↓ Δ). This functor is left adjoint
to the corresponding forgetful functor.
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the final topology (or strong topology or colimit topology or inductive topology) on a set
, with respect to a family of functions into , is the finest topology on X which makes those functions continuous.Definition
Given a set and a family of topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s
with functionsthe final topology
on is the finest topology such that eachis continuous.
Explicitly, the final topology may be described as follows: a subset U of X is open if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
is open in Yi for each i ∈ I.Examples
- The quotient topology is the final topology on the quotient space with respect to the quotient map.
- The disjoint unionDisjoint union (topology)In general topology and related areas of mathematics, the disjoint union of a family of topological spaces is a space formed by equipping the disjoint union of the underlying sets with a natural topology called the disjoint union topology...
is the final topology with respect to the family of canonical injections. - More generally, a topological space is coherentCoherent topologyIn topology, a coherent topology is one that is uniquely determined by a family of subspaces. Loosely speaking, a topological space is coherent with a family of subspaces if it is a topological union of those subspaces.-Definition:...
with a family of subspaces if it has the final topology coinduced by the inclusion maps. - The direct limitDirect limitIn mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of any direct system of spaces and continuous maps is the set-theoretic direct limit together with the final topology determined by the canonical morphisms. - Given a familyFamily of setsIn set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
of topologies {τi} on a fixed set X the final topology on X with respect to the functions idX : (X, τi) → X is the infimumInfimumIn mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
(or meet) of the topologies {τi} in the lattice of topologies on X. That is, the final topology τ is the intersectionIntersection (set theory)In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of the topologies {τi}.
Properties
A subset of is closed/open if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
its preimage under fi is closed/open in
for each i ∈ I.The final topology on X can be characterized by the following universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
: a function
from to some space is continuous if and only if is continuous for each i ∈ I.If the family of maps fi covers X (i.e. each x in X lies in the image of some fi) then the map f will be a quotient map if and only if X has the final topology determined by the maps fi.
Categorical description
In the language of category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the final topology construction can be described as follows. Let Y be a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from a discrete category
Discrete category
In mathematics, especially category theory, a discrete category is a category whose only morphisms are the identity morphisms. It is the simplest kind of category...
J to the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
Top which selects the spaces Yi for i in J. Let Δ be the diagonal functor from Top to the functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
TopJ (this functor sends each space X to the constant functor to X). The comma category
Comma category
In mathematics, a comma category is a construction in category theory. It provides another way of looking at morphisms: instead of simply relating objects of a category to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W...
(Y ↓ Δ) is then the category of cones from Y, i.e. objects in (Y ↓ Δ) are pairs (X, f) where fi : Yi → X is a family of continuous maps to X. If U is the forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
from Top to Set and Δ′ is the diagonal functor from Set to SetJ then the comma category (UY ↓ Δ′) is the category of all cones from UY. The final topology construction can then be described as a functor from (UY ↓ Δ′) to (Y ↓ Δ). This functor is left adjoint
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
to the corresponding forgetful functor.