.gif)
Disjoint union (topology)
Encyclopedia
In general topology
and related areas of mathematics
, the disjoint union (also called the direct sum, free union, free sum, topological sum, or coproduct) of a family of topological space
s is a space formed by equipping the disjoint union
of the underlying sets with a natural topology
called the disjoint union topology. Roughly speaking, two or more spaces may be considered together, each looking as it would alone.
The name coproduct originates from the fact that the disjoint union is the categorical dual of the product space construction.
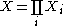
be the disjoint union
of the underlying sets. For each i in I, let
be the canonical injection (defined by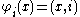
). The disjoint union topology on X is defined as the finest topology on X for which the canonical injections are continuous (i.e. the final topology
for the family of functions {φi}).
Explicitly, the disjoint union topology can be described as follows. A subset U of X is open
in X if and only if
its preimage
is open in Xi for each i ∈ I.
Yet another formulation is that a subset V of X is open relative to X iff
its intersection with Xi is open relative to Xi for each i.
: If Y is a topological space, and fi : Xi → Y is a continuous map for each i ∈ I, then there exists precisely one continuous map f : X → Y such that the following set of diagrams commute
:
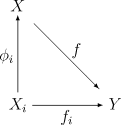This shows that the disjoint union is the coproduct
in the category of topological spaces
. It follows from the above universal property that a map f : X → Y is continuous iff
fi = f o φi is continuous for all i in I.
In addition to being continuous, the canonical injections φi : Xi → X are open and closed maps
. It follows that the injections are topological embeddings so that each Xi may be canonically thought of as a subspace of X.
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
and related areas of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the disjoint union (also called the direct sum, free union, free sum, topological sum, or coproduct) of a family of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s is a space formed by equipping the disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of the underlying sets with a natural topology
Natural topology
In any domain of mathematics, a space has a natural topology if there is a topology on the space which is "best adapted" to its study within the domain in question...
called the disjoint union topology. Roughly speaking, two or more spaces may be considered together, each looking as it would alone.
The name coproduct originates from the fact that the disjoint union is the categorical dual of the product space construction.
Definition
Let {Xi : i ∈ I} be a family of topological spaces indexed by I. Letbe the disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of the underlying sets. For each i in I, let
be the canonical injection (defined by
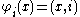). The disjoint union topology on X is defined as the finest topology on X for which the canonical injections are continuous (i.e. the final topologyFinal topology
In general topology and related areas of mathematics, the final topology on a set X, with respect to a family of functions into X, is the finest topology on X which makes those functions continuous.- Definition :Given a set X and a family of topological spaces Y_i with functionsf_i: Y_i \to Xthe...
for the family of functions {φi}).
Explicitly, the disjoint union topology can be described as follows. A subset U of X is open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in X if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
its preimage
is open in Xi for each i ∈ I.Yet another formulation is that a subset V of X is open relative to X iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
its intersection with Xi is open relative to Xi for each i.
Properties
The disjoint union space X, together with the canonical injections, can be characterized by the following universal propertyUniversal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
: If Y is a topological space, and fi : Xi → Y is a continuous map for each i ∈ I, then there exists precisely one continuous map f : X → Y such that the following set of diagrams commute
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
in the category of topological spaces
Category of topological spaces
In mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
. It follows from the above universal property that a map f : X → Y is continuous iff
IFF
IFF, Iff or iff may refer to:Technology/Science:* Identification friend or foe, an electronic radio-based identification system using transponders...
fi = f o φi is continuous for all i in I.
In addition to being continuous, the canonical injections φi : Xi → X are open and closed maps
Open and closed maps
In topology, an open map is a function between two topological spaces which maps open sets to open sets. That is, a function f : X → Y is open if for any open set U in X, the image f is open in Y. Likewise, a closed map is a function which maps closed sets to closed sets...
. It follows that the injections are topological embeddings so that each Xi may be canonically thought of as a subspace of X.
Examples
If each Xi is homeomorphic to a fixed space A, then the disjoint union X will be homeomorphic to A × I where I is given the discrete topology.Preservation of topological properties
- every disjoint union of discrete spaceDiscrete spaceIn topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
s is discrete - Separation
- every disjoint union of T0 spaces is T0
- every disjoint union of T1 spaceT1 spaceIn topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
s is T1 - every disjoint union of Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s is Hausdorff
- Connectedness
- the disjoint union of two or more nonempty topological spaces is disconnected
See also
- product topologyProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
, the dual construction - subspace topologySubspace topologyIn topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
and its dual quotient topology - topological union, a generalization to the case where the pieces are not disjoint