Universal property
Encyclopedia
In various branches of mathematics
, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory
to make this notion precise and to study it abstractly.
This article gives a general treatment of universal properties. To understand the concept, it is useful to study several examples first, of which there are many: all free object
s, direct product
and direct sum
, free group
, free lattice
, Grothendieck group
, product topology
, Stone–Čech compactification
, tensor product
, inverse limit
and direct limit
, kernel
and cokernel
, pullback
, pushout
and equalizer.
from a category
D to a category C, and let X be an object of C. Consider the following dual (opposite) notions:
An initial morphism from X to U is an initial object
in the category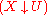
of morphisms from X to U
. In other words, it consists of a pair (A, φ) where A is an object of D and φ: X → U(A) is a morphism in C, such that the following initial property is satisfied:
A terminal morphism from U to X is a terminal object in the comma category
of morphisms from U to X. In other words, it consists of a pair (A, φ) where A is an object of D and φ: U(A) → X is a morphism in C, such that the following terminal property is satisfied:
The term universal morphism refers either to an initial morphism or a terminal morphism, and the term universal property refers either to an initial property or a terminal property. In each definition, the existence of the morphism g intuitively expresses the fact that (A, φ) is "general enough", while the uniqueness of the morphism ensures that (A, φ) is "not too general".
Note: some authors may call only one of these constructions a universal morphism and the other one a co-universal morphism. Which is which depends on the author, although in order to be consistent with the naming of limits and colimits
the latter construction should be named universal and the former couniversal. This article uses the unambiguous terminology of initial and terminal objects.
K-Vect over a field
K and let D be the category of algebras
K-Alg over K (assumed to be unital and associative
). Let
be the forgetful functor
which assigns to each algebra its underlying vector space.
Given any vector space
V over K we can construct the tensor algebra
T(V) of V. The tensor algebra is characterized by the fact:
This statement is an initial property of the tensor algebra since it expresses the fact that the pair (T(V), i), where i : V → T(V) is the inclusion map, is an initial morphism from the vector space V to the functor U.
Since this construction works for any vector space V, we conclude that T is a functor from K-Vect to K-Alg. This means that T is left adjoint to the forgetful functor U (see the section below on relation to adjoint functors).
in Set, the direct product
in Grp, or the product topology
in Top.
Let X and Y be objects of a category D. The product of X and Y is an object X × Y together with two morphisms
such that for any other object Z of D and morphisms f : Z → X and g : Z → Y there exists a unique morphism h : Z → X × Y such that f = π1∘h and g = π2∘h.
To understand this characterization as a terminal property we take the category C to be the product category
D × D and define the diagonal functor
by Δ(X) = (X, X) and Δ(f : X → Y) = (f, f). Then (X × Y, (π1, π2)) is a terminal morphism from Δ to the object (X, Y) of D × D. This is just a restatement of the above since the pair (f, g) represents an (arbitrary) morphism from Δ(Z) to (X, Y).
in category theory. One can generalize the above example to arbitrary limits and colimits.
Let J and C be categories with J a small index category and let CJ be the corresponding functor category
. The diagonal functor
is the functor that maps each object N in C to the constant functor Δ(N): J → C to N (i.e. Δ(N)(X) = N for each X in J).
Given a functor F : J → C (thought of as an object in CJ), the limit of F, if it exists, is nothing but a terminal morphism from Δ to F. Dually, the colimit of F is an initial morphism from F to Δ.
a unique isomorphism
: if (A′, φ′) is another such pair, then there exists a unique isomorphism k: A → A′ such that φ′ = U(k)φ. This is easily seen by substituting (A′, φ′) for (Y, f) in the definition of the initial property.
It is the pair (A, φ) which is essentially unique in this fashion. The object A itself is only unique up to isomorphism. Indeed, if (A, φ) is an initial morphism and k: A → A′ is any isomorphism then the pair (A′, φ′), where φ′ = U(k)φ, is also an initial morphism.
The dual statements are also equivalent:
If every object Xi of C admits a initial morphism to U, then the assignment
and 
defines a functor V from C to D. The maps φi then define a natural transformation
from 1C (the identity functor on C) to UV. The functors (V, U) are then a pair of adjoint functors, with V left-adjoint to U and U right-adjoint to V.
Similar statements apply to the dual situation of terminal morphisms from U. If such morphisms exist for every X in C one obtains a functor V: C → D which is right-adjoint to U (so U is left-adjoint to V).
Indeed, all pairs of adjoint functors arise from universal constructions in this manner. Let F and G be a pair of adjoint functors with unit η and co-unit ε (see the article on adjoint functors
for the definitions). Then we have a universal morphism for each object in C and D:
Universal constructions are more general than adjoint functor pairs: a universal construction is like an optimization problem; it gives rise to an adjoint pair if and only if this problem has a solution for every object of C (equivalently, every object of D).
in 1948. They were later used extensively by Bourbaki. The closely related concept of adjoint functors was introduced independently by Daniel Kan
in 1958.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
to make this notion precise and to study it abstractly.
This article gives a general treatment of universal properties. To understand the concept, it is useful to study several examples first, of which there are many: all free object
Free object
In mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
s, direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
and direct sum
Direct sum
In mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
, free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
, free lattice
Free lattice
In mathematics, in the area of order theory, a free lattice is the free object corresponding to a lattice. As free objects, they have the universal property. The word problem for free lattices is also challenging.-Formal definition:...
, Grothendieck group
Grothendieck group
In mathematics, the Grothendieck group construction in abstract algebra constructs an abelian group from a commutative monoid in the best possible way...
, product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
, Stone–Čech compactification
Stone–Cech compactification
In the mathematical discipline of general topology, Stone–Čech compactification is a technique for constructing a universal map from a topological space X to a compact Hausdorff space βX...
, tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
, inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
and direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
, kernel
Kernel (category theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
and cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
, pullback
Pullback (category theory)
In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain; it is the limit of the cospan X \rightarrow Z \leftarrow Y...
, pushout
Pushout (category theory)
In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
and equalizer.
Motivation
Before giving a formal definition of universal properties, we offer some motivation for studying such constructions.- The concrete details of a given construction may be messy, but if the construction satisfies a universal property, one can forget all those details: all there is to know about the construct is already contained in the universal property. Proofs often become short and elegant if the universal property is used rather than the concrete details. For example, the tensor algebra of a vector space is slightly painful to actually construct, but using its universal property makes it much easier to deal with.
- Universal properties define objects uniquely up to isomorphism. Therefore, one strategy to prove that two objects are isomorphic is to show that they satisfy the same universal property.
- Universal constructions are functorial in nature: if one can carry out the construction for every object in a category C then one obtains a functorFunctorIn category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
on C. Furthermore, this functor is a right or left adjointAdjoint functorsIn mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
to the functor U used in the definition of the universal property. - Universal properties occur everywhere in mathematics. By understanding their abstract properties, one obtains information about all these constructions and can avoid repeating the same analysis for each individual instance.
Formal definition
Suppose that U: D → C is a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
D to a category C, and let X be an object of C. Consider the following dual (opposite) notions:
An initial morphism from X to U is an initial object
Initial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
in the category
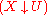of morphisms from X to UComma category
In mathematics, a comma category is a construction in category theory. It provides another way of looking at morphisms: instead of simply relating objects of a category to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W...
. In other words, it consists of a pair (A, φ) where A is an object of D and φ: X → U(A) is a morphism in C, such that the following initial property is satisfied:
- Whenever Y is an object of D and f: X → U(Y) is a morphism in C, then there exists a unique morphism g: A → Y such that the following diagram commutesCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
A terminal morphism from U to X is a terminal object in the comma category
Comma category
In mathematics, a comma category is a construction in category theory. It provides another way of looking at morphisms: instead of simply relating objects of a category to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W...
of morphisms from U to X. In other words, it consists of a pair (A, φ) where A is an object of D and φ: U(A) → X is a morphism in C, such that the following terminal property is satisfied:
- Whenever Y is an object of D and f: U(Y) → X is a morphism in C, then there exists a unique morphism g: Y → A such that the following diagram commutes:
The term universal morphism refers either to an initial morphism or a terminal morphism, and the term universal property refers either to an initial property or a terminal property. In each definition, the existence of the morphism g intuitively expresses the fact that (A, φ) is "general enough", while the uniqueness of the morphism ensures that (A, φ) is "not too general".
Duality
Since the notions of initial and terminal are dual, it is often enough to discuss only one of them, and simply reverse arrows in C for the dual discussion. Alternatively, the word universal is often used in place of both words.Note: some authors may call only one of these constructions a universal morphism and the other one a co-universal morphism. Which is which depends on the author, although in order to be consistent with the naming of limits and colimits
Limit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
the latter construction should be named universal and the former couniversal. This article uses the unambiguous terminology of initial and terminal objects.
Examples
Below are a few worked examples, to highlight the general idea. The reader can construct numerous other examples by consulting the articles mentioned in the introduction.Tensor algebras
Let C be the category of vector spacesCategory of vector spaces
In mathematics, especially category theory, the category K-Vect has all vector spaces over a fixed field K as objects and K-linear transformations as morphisms...
K-Vect over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K and let D be the category of algebras
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
K-Alg over K (assumed to be unital and associative
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
). Let
- U : K-Alg → K-Vect
be the forgetful functor
Forgetful functor
In mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
which assigns to each algebra its underlying vector space.
Given any vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V over K we can construct the tensor algebra
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
T(V) of V. The tensor algebra is characterized by the fact:
- “Any linear map from V to an algebra A can be uniquely extended to an algebra homomorphismAlgebra homomorphismA homomorphism between two algebras, A and B, over a field K, is a map F:A\rightarrow B such that for all k in K and x,y in A,* F = kF* F = F + F...
from T(V) to A.”
This statement is an initial property of the tensor algebra since it expresses the fact that the pair (T(V), i), where i : V → T(V) is the inclusion map, is an initial morphism from the vector space V to the functor U.
Since this construction works for any vector space V, we conclude that T is a functor from K-Vect to K-Alg. This means that T is left adjoint to the forgetful functor U (see the section below on relation to adjoint functors).
Products
A categorical product can be characterized by a terminal property. For concreteness, one may consider the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
in Set, the direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
in Grp, or the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
in Top.
Let X and Y be objects of a category D. The product of X and Y is an object X × Y together with two morphisms
- π1 : X × Y → X
- π2 : X × Y → Y
such that for any other object Z of D and morphisms f : Z → X and g : Z → Y there exists a unique morphism h : Z → X × Y such that f = π1∘h and g = π2∘h.
To understand this characterization as a terminal property we take the category C to be the product category
Product category
In the mathematical field of category theory, the product of two categories C and D, denoted and called a product category, is a straightforward extension of the concept of the Cartesian product of two sets.-Definition:...
D × D and define the diagonal functor
- Δ : D → D × D
by Δ(X) = (X, X) and Δ(f : X → Y) = (f, f). Then (X × Y, (π1, π2)) is a terminal morphism from Δ to the object (X, Y) of D × D. This is just a restatement of the above since the pair (f, g) represents an (arbitrary) morphism from Δ(Z) to (X, Y).
Limits and colimits
Categorical products are a particular kind of limitLimit (category theory)
In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
in category theory. One can generalize the above example to arbitrary limits and colimits.
Let J and C be categories with J a small index category and let CJ be the corresponding functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
. The diagonal functor
- Δ : C → CJ
is the functor that maps each object N in C to the constant functor Δ(N): J → C to N (i.e. Δ(N)(X) = N for each X in J).
Given a functor F : J → C (thought of as an object in CJ), the limit of F, if it exists, is nothing but a terminal morphism from Δ to F. Dually, the colimit of F is an initial morphism from F to Δ.
Existence and uniqueness
Defining a quantity does not guarantee its existence. Given a functor U and an object X as above, there may or may not exist an initial morphism from X to U. If, however, an initial morphism (A, φ) does exist then it is essentially unique. Specifically, it is unique up toUp to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a unique isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
: if (A′, φ′) is another such pair, then there exists a unique isomorphism k: A → A′ such that φ′ = U(k)φ. This is easily seen by substituting (A′, φ′) for (Y, f) in the definition of the initial property.
It is the pair (A, φ) which is essentially unique in this fashion. The object A itself is only unique up to isomorphism. Indeed, if (A, φ) is an initial morphism and k: A → A′ is any isomorphism then the pair (A′, φ′), where φ′ = U(k)φ, is also an initial morphism.
Equivalent formulations
The definition of a universal morphism can be rephrased in a variety of ways. Let U be a functor from D to C, and let X be an object of C. Then the following statements are equivalent:- (A, φ) is an initial morphism from X to U
- (A, φ) is an initial objectInitial objectIn category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
of the comma categoryComma categoryIn mathematics, a comma category is a construction in category theory. It provides another way of looking at morphisms: instead of simply relating objects of a category to one another, morphisms become objects in their own right. This notion was introduced in 1963 by F. W...
(X ↓ U) - (A, φ) is a representationRepresentable functorIn mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
of HomC(X, U—)
The dual statements are also equivalent:
- (A, φ) is a terminal morphism from U to X
- (A, φ) is a terminal object of the comma category (U ↓ X)
- (A, φ) is a representation of HomC(U—, X)
Relation to adjoint functors
Suppose (A1, φ1) is an initial morphism from X1 to U and (A2, φ2) is an initial morphism from X2 to U. By the initial property, given any morphism h: X1 → X2 there exists a unique morphism g: A1 → A2 such that the following diagram commutes:If every object Xi of C admits a initial morphism to U, then the assignment
and defines a functor V from C to D. The maps φi then define a natural transformationNatural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
from 1C (the identity functor on C) to UV. The functors (V, U) are then a pair of adjoint functors, with V left-adjoint to U and U right-adjoint to V.
Similar statements apply to the dual situation of terminal morphisms from U. If such morphisms exist for every X in C one obtains a functor V: C → D which is right-adjoint to U (so U is left-adjoint to V).
Indeed, all pairs of adjoint functors arise from universal constructions in this manner. Let F and G be a pair of adjoint functors with unit η and co-unit ε (see the article on adjoint functors
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
for the definitions). Then we have a universal morphism for each object in C and D:
- For each object X in C, (F(X), ηX) is an initial morphism from X to G. That is, for all f: X → G(Y) there exists a unique g: F(X) → Y for which the following diagrams commute.
- For each object Y in D, (G(Y), εY) is a terminal morphism from F to Y. That is, for all g: F(X) → Y there exists a unique f: X → G(Y) for which the following diagrams commute.
Universal constructions are more general than adjoint functor pairs: a universal construction is like an optimization problem; it gives rise to an adjoint pair if and only if this problem has a solution for every object of C (equivalently, every object of D).
History
Universal properties of various topological constructions were presented by Pierre SamuelPierre Samuel
Pierre Samuel was a French mathematician, known for his work in commutative algebra and its applications to algebraic geometry. The two-volume work Commutative Algebra that he wrote with Oscar Zariski is a classic. Other books of his covered projective geometry and algebraic number theory...
in 1948. They were later used extensively by Bourbaki. The closely related concept of adjoint functors was introduced independently by Daniel Kan
Daniel Kan
Daniel Marinus Kan is a mathematician working in homotopy theory. He has been a prolific contributor to the field for the last five decades, having authored or coauthored several dozen research papers and monographs. The general theme of his career has been abstract homotopy theory.He is an...
in 1958.
See also
- Free objectFree objectIn mathematics, the idea of a free object is one of the basic concepts of abstract algebra. It is a part of universal algebra, in the sense that it relates to all types of algebraic structure . It also has a formulation in terms of category theory, although this is in yet more abstract terms....
- Monad (category theory)Monad (category theory)In category theory, a branch of mathematics, a monad, Kleisli triple, or triple is an functor, together with two natural transformations...
- Variety of algebras
- Cartesian closed categoryCartesian closed categoryIn category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...