.gif)
Limit (category theory)
Encyclopedia
In category theory
, a branch of mathematics
, the abstract notion of a limit captures the essential properties of universal constructions such as products
and inverse limit
s.
The dual notion of a colimit generalizes constructions such as disjoint union
s, direct sum
s, coproduct
s, pushout
s and direct limit
s.
Limits and colimits, like the strongly related notions of universal properties
and adjoint functors
, exist at a high level of abstraction. In order to understand them, it is helpful to first study the specific examples these concepts are meant to generalize.
C are defined by means of diagrams in C. Formally, a diagram
of type J in C is a functor
from J to C:
The category J is thought of as index category, and the diagram F is thought of as indexing a collection of objects and morphisms in C patterned on J. The actual objects and morphisms in J are largely irrelevant—only the way in which they are interrelated matters.
One is most often interested in the case where the category J is a small or even finite category. A diagram is said to be small or finite whenever J is.
to F is an object N of C together with a family ψX : N → F(X) of morphisms indexed by the objects of J, such that for every morphism f : X → Y in J, we have F(f) o ψX = ψY.
A limit of the diagram F : J → C is a cone (L, φ) to F such that for any other cone (N, ψ) to F there exists a unique morphism u : N → L such that φX o u = ψX for all X in J.
.svg.png) One says that the cone (N, ψ) factors through the cone (L, φ) with
One says that the cone (N, ψ) factors through the cone (L, φ) with
the unique factorization u. The morphism u is sometimes called the mediating morphism.
Limits are also referred to as universal cones, since they are characterized by a universal property
(see below for more information). As with every universal property, the above definition describes a balanced state of generality: The limit object L has to be general enough to allow any other cone to factor through it; on the other hand, L has to be sufficiently specific, so that only one such factorization is possible for every cone.
Limits may also be characterized as terminal objects in the category of cones to F.
It is possible that a diagram does not have a limit at all. However, if a diagram does have a limit then this limit is essentially unique: it is unique up to
a unique isomorphism. For this reason one often speaks of the limit of F.
of limits and cones are colimits and co-cones. Although it is straightforward to obtain the definitions of these by inverting all morphisms in the above definitions, we will explicitly state them here:
A co-cone of a diagram F : J → C is an object N of C together with a family of morphisms
for every object X of J, such that for every morphism f : X → Y in J, we have ψY o F(f)= ψX.
A colimit of a diagram F : J → C is a co-cone (L, ) of F such that for any other co-cone (N, ψ) of F there exists a unique morphism u : L → N such that u o
) of F such that for any other co-cone (N, ψ) of F there exists a unique morphism u : L → N such that u o  X = ψX for all X in J.
X = ψX for all X in J.
.svg.png) Colimits are also referred to as universal co-cones. They can be characterized as initial object
Colimits are also referred to as universal co-cones. They can be characterized as initial object
s in the category of co-cones from F.
As with limits, if a diagram F has a colimit then this colimit is unique up to a unique isomorphism.
G. If we let J be the free category generated by G, there is a universal diagram F : J → C whose image contains G. The limit (or colimit) of this diagram is the same as the limit (or colimit) of the original collection of objects and morphisms.
Weak limit and weak colimits are defined like limits and colimits, except that the uniqueness property of the mediating morphism is dropped.
A category C is said to have limits of type J if every diagram of type J has a limit in C. Specifically, a category C is said to
A complete category
is a category that has all small limits (i.e. all limits of type J for every small category J).
One can also make the dual definitions. A category has colimits of type J if every diagram of type J has a colimit in C. A cocomplete category is one that has all small colimits.
The existence theorem for limits states that if a category C has equalizers and all products indexed by the classes Ob(J) and Hom(J), then C has all limits of type J. In this case, the limit of a diagram F : J → C can be constructed as the equalizer of the two morphisms
given (in component form) by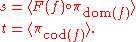
There is a dual existence theorem for colimits in terms of coequalizers and coproducts. Both of these theorems give sufficient but not necessary conditions for the existence of all (co)limits of type J.
CJ may be thought of the category of all diagrams of type J in C. The diagonal functor
is the functor that maps each object N in C to the constant functor Δ(N) : J → C to N. That is, Δ(N)(X) = N for each object X in J and Δ(N)(f) = idN for each morphism f in J.
Given a diagram F: J → C (thought of as an object in CJ), a natural transformation
ψ : Δ(N) → F (which is just a morphism in the category CJ) is the same thing as a cone from N to F. The components of ψ are the morphisms ψX : N → F(X). Dually, a natural transformation ψ : F → Δ(N) is the same thing as a co-cone from F to N.
The definitions of limits and colimits can then be restated in the form:

which assigns each diagram its limit and each natural transformation
η : F → G the unique morphism lim η : lim F → lim G commuting with the corresponding universal cones. This functor is right adjoint to the diagonal functor Δ : C → CJ.
This adjunction gives a bijection between the set of all morphisms from N to lim F and the set of all cones from N to F
which is natural in the variables N and F. The counit of this adjunction is simply the universal cone from lim F to F. If the index category J is connected (and nonempty) then the unit of the adjunction is an isomorphism so that lim is a left inverse of Δ. This fails if J is not connected. For example, if J is a discrete category, the components of the unit are the diagonal morphisms δ : N → NJ.
Dually, if every diagram of type J has a colimit in C (for J small) there exists a colimit functor
which assigns each diagram its colimit. This functor is left adjoint to the diagonal functor Δ : C → CJ, and one has a natural isomorphism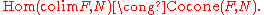
The unit of this adjunction is the universal cocone from F to colim F. If J is connected (and nonempty) then the counit is an isomorphism, so that colim is a left inverse of Δ.
Note that both the limit and the colimit functors are covariant functors.
s to relate limits and colimits in a category C to limits in Set, the category of sets
. This follows, in part, from the fact the covariant Hom functor Hom(N, –) : C → Set preserves all limits in C. By duality, the contravariant Hom functor must take colimits to limits.
If a diagram F : J → C has a limit in C, denoted by lim F, there is a canonical isomorphism
which is natural in the variable N. Here the functor Hom(N, F–) is the composition of the Hom functor Hom(N, –) with F. This isomorphism is the unique one which respects the limiting cones.
One can use the above relationship to define the limit of F in C. The first step is to observe that the limit of the functor Hom(N, F–) can be identified with the set of all cones from N to F:
The limiting cone is given by the family of maps πX : Cone(N, F) → Hom(N, FX) where πX(ψ) = ψX. If one is given an object L of C together with a natural isomorphism Φ : Hom(–, L) → Cone(–, F), the object L will be a limit of F with the limiting cone given by ΦL(idL). In fancy language, this amounts to saying that a limit of F is a representation
of the functor Cone(–, F) : C → Set.
Dually, if a diagram F : J → C has a colimit in C, denoted colim F, there is a unique canonical isomorphism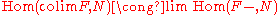
which is natural in the variable N and respects the colimiting cones. Identifying the limit of Hom(F–, N) with the set Cocone(F, N), this relationship can be used to define the colimit of the diagram F as a representation of the functor Cocone(F, –).
. For any bifunctor
there is a natural isomorphism

In words, filtered colimits in Set commute with finite limits.
then by composition (recall that a diagram is just a functor) one obtains a diagram GF : J → D. A natural question is then:
preserves the limits of F.)
A functor G is said to preserve all limits of type J if it preserves the limits of all diagrams F : J → C. For example, one can say that G preserves products, equalizers, pullbacks, etc. A continuous functor is one that preserves all small limits.
One can make analogous definitions for colimits. For instance, a functor G preserves the colimits of F if G(L, φ) is a colimit of GF whenever (L, φ) is a colimit of F. A cocontinuous functor is one that preserves all small colimits.
If C is a complete category
, then, by the above existence theorem for limits, a functor G : C → D is continuous if and only if it preserves (small) products and equalizers. Dually, G is cocontinuous if and only if it preserves (small) coproducts and coequalizers.
An important property of adjoint functors
is that every right adjoint functor is continuous and every left adjoint functor is cocontinuous. Since adjoint functors exist in abundance, this gives numerous examples of continuous and cocontinuous functors.
For a given diagram F : J → C and functor G : C → D, if both F and GF have specified limits there is a unique canonical morphism
which respects the corresponding limit cones. The functor G preserves the limits of F if and only this map is an isomorphism. If the categories C and D have all limits of type J then lim is a functor and the morphisms τF form the components of a natural transformation
The functor G preserves all limits of type J if and only if τ is a natural isomorphism. In this sense, the functor G can be said to commute with limits (up to
a canonical natural isomorphism).
Preservation of limits and colimits is a concept that only applies to covariant functors. For contravariant functors the corresponding notions would be a functor that takes colimits to limits, or one that takes limits to colimits.
A functor G lifts limits uniquely for a diagram F if there is a unique preimage cone (L′, φ′) such that (L′, φ′) is a limit of F and G(L′, φ′) = (L, φ). One can show that G lifts limits uniquely if and only if it lifts limits and is amnestic
.
Lifting of limits is clearly related to preservation of limits. If G lifts limits for a diagram F and GF has a limit, then F also has a limit and G preserves the limits of F. It follows that:
The dual statements for colimits are equally valid.
Dually, one can define creation and reflection of colimits.
The following statements are easily seen to be equivalent:
There are examples of functors which lift limits uniquely but neither create nor reflect them.
There are several ways to remember the modern terminology. First of all,
are types of colimits, whereas
are types of limits. Second, the prefix "co" implies "first variable of the ". Terms like "cohomology" and "cofibration" all have a slightly stronger association with the first variable, i.e., the contravariant variable, of the
". Terms like "cohomology" and "cofibration" all have a slightly stronger association with the first variable, i.e., the contravariant variable, of the  bifunctor.
bifunctor.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the abstract notion of a limit captures the essential properties of universal constructions such as products
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
and inverse limit
Inverse limit
In mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
s.
The dual notion of a colimit generalizes constructions such as disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
s, direct sum
Direct sum
In mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
s, coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
s, pushout
Pushout (category theory)
In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
s and direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
s.
Limits and colimits, like the strongly related notions of universal properties
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
and adjoint functors
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
, exist at a high level of abstraction. In order to understand them, it is helpful to first study the specific examples these concepts are meant to generalize.
Definition
Limits and colimits in a categoryCategory (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
C are defined by means of diagrams in C. Formally, a diagram
Diagram (category theory)
In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function...
of type J in C is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from J to C:
- F : J → C.
The category J is thought of as index category, and the diagram F is thought of as indexing a collection of objects and morphisms in C patterned on J. The actual objects and morphisms in J are largely irrelevant—only the way in which they are interrelated matters.
One is most often interested in the case where the category J is a small or even finite category. A diagram is said to be small or finite whenever J is.
Limits
Let F : J → C be a diagram of type J in a category C. A coneCone (category theory)
In category theory, a branch of mathematics, the cone of a functor is an abstract notion used to define the limit of that functor. Cones make other appearances in category theory as well.-Definition:...
to F is an object N of C together with a family ψX : N → F(X) of morphisms indexed by the objects of J, such that for every morphism f : X → Y in J, we have F(f) o ψX = ψY.
A limit of the diagram F : J → C is a cone (L, φ) to F such that for any other cone (N, ψ) to F there exists a unique morphism u : N → L such that φX o u = ψX for all X in J.
.svg.png)
the unique factorization u. The morphism u is sometimes called the mediating morphism.
Limits are also referred to as universal cones, since they are characterized by a universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
(see below for more information). As with every universal property, the above definition describes a balanced state of generality: The limit object L has to be general enough to allow any other cone to factor through it; on the other hand, L has to be sufficiently specific, so that only one such factorization is possible for every cone.
Limits may also be characterized as terminal objects in the category of cones to F.
It is possible that a diagram does not have a limit at all. However, if a diagram does have a limit then this limit is essentially unique: it is unique up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a unique isomorphism. For this reason one often speaks of the limit of F.
Colimits
The dual notionsDual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
of limits and cones are colimits and co-cones. Although it is straightforward to obtain the definitions of these by inverting all morphisms in the above definitions, we will explicitly state them here:
A co-cone of a diagram F : J → C is an object N of C together with a family of morphisms
- ψX : F(X) → N
for every object X of J, such that for every morphism f : X → Y in J, we have ψY o F(f)= ψX.
A colimit of a diagram F : J → C is a co-cone (L,
 ) of F such that for any other co-cone (N, ψ) of F there exists a unique morphism u : L → N such that u o
) of F such that for any other co-cone (N, ψ) of F there exists a unique morphism u : L → N such that u o  X = ψX for all X in J.
X = ψX for all X in J..svg.png)
Initial object
In category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
s in the category of co-cones from F.
As with limits, if a diagram F has a colimit then this colimit is unique up to a unique isomorphism.
Variations
Limits and colimits can also be defined for collections of objects and morphisms without the use of diagrams. The definitions are the same (note that in definitions above we never needed to use composition of morphisms in J). This variation, however, adds no new information. Any collection of objects and morphisms defines a (possibly large) directed graphDirected graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
G. If we let J be the free category generated by G, there is a universal diagram F : J → C whose image contains G. The limit (or colimit) of this diagram is the same as the limit (or colimit) of the original collection of objects and morphisms.
Weak limit and weak colimits are defined like limits and colimits, except that the uniqueness property of the mediating morphism is dropped.
Limits
The definition of limits is general enough to subsume several constructions useful in practical settings. In the following we will consider the limit (L, φ) of a diagram F : J → C.- Terminal objects. If J is the empty category there is only one diagram of type J: the empty one (similar to the empty functionEmpty functionIn mathematics, an empty function is a function whose domain is the empty set. For each set A, there is exactly one such empty functionf_A: \varnothing \rightarrow A....
in set theory). A cone to the empty diagram is essentially just an object of C. The limit of F is any object that has a unique factorization through any other object. This is just the definition of a terminal object. - ProductsProduct (category theory)In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
. If J is a discrete categoryDiscrete categoryIn mathematics, especially category theory, a discrete category is a category whose only morphisms are the identity morphisms. It is the simplest kind of category...
then a diagram F is essentially nothing but a familyIndexed familyIn mathematics, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers....
of objects of C, indexed by J. The limit L of F is called the product of these objects. The cone φ consists of a family of morphisms φX : L → F(X) called the projections of the product. In the category of setsCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, for instance, the products are given by Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
s and the projections are just the natural projections onto the various factors.- Powers. A special case of a product is when the diagram F is a constant functor to an object X of C. The limit of this diagram is called the Jth power of X and denoted XJ.
- Equalizers. If J is a category with two objects and two parallel morphisms from object 1 to object 2 then a diagram of type J is a pair of parallel morphisms in C. The limit L of such a diagram is called an equalizer of those morphisms.
- KernelKernel (category theory)In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
s. A kernel is a special case of an equalizer where one of the morphisms is a zero morphismZero morphismIn category theory, a zero morphism is a special kind of morphism exhibiting properties like those to and from a zero object.Suppose C is a category, and f : X → Y is a morphism in C...
.
- Kernel
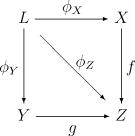
- PullbacksPullback (category theory)In category theory, a branch of mathematics, a pullback is the limit of a diagram consisting of two morphisms f : X → Z and g : Y → Z with a common codomain; it is the limit of the cospan X \rightarrow Z \leftarrow Y...
. Let F be a diagram that picks out three objects X, Y, and Z in C, where the only non-identity morphisms are f : X → Z and g : Y → Z. The limit L of F is called a pullback or a fiber product. It can nicely be visualized as a commutative squareCommutative diagramIn mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:

- Inverse limitInverse limitIn mathematics, the inverse limit is a construction which allows one to "glue together" several related objects, the precise manner of the gluing process being specified by morphisms between the objects...
s. Let J be a directedDirected setIn mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
poset (considered as a small category by adding arrows i → j if and only if i ≤ j) and let F : Jop → C be a diagram. The limit of F is called (confusingly) an inverse limit, projective limit, or directed limit. - If J = 1, the category with a single object and morphism, then a diagram of type J is essentially just an object of C. A cone to an object X is just a morphism with codomain X. A morphism f : Y → X is a limit of the diagram X if and only if f is an isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
. More generally, if J is any category with an initial objectInitial objectIn category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
i, then any diagram of type J has a limit, namely any object isomorphic to F(i). Such an isomorphism uniquely determines a universal cone to F.
Colimits
Examples of colimits are given by the dual versions of the examples above:- Initial objectInitial objectIn category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
s are colimits of empty diagrams. - CoproductCoproductIn category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
s are colimits of diagrams indexed by discrete categories.- Copowers are colimits of constant diagrams from discrete categories.
- CoequalizerCoequalizerIn category theory, a coequalizer is a generalization of a quotient by an equivalence relation to objects in an arbitrary category...
s are colimits of a parallel pair of morphisms.- CokernelCokernelIn mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
s are coequalizers of a morphism and a parallel zero morphism.
- Cokernel
- PushoutsPushout (category theory)In category theory, a branch of mathematics, a pushout is the colimit of a diagram consisting of two morphisms f : Z → X and g : Z → Y with a common domain: it is the colimit of the span X \leftarrow Z \rightarrow Y.The pushout is the...
are colimits of a pair of morphisms with common domain. - Direct limitDirect limitIn mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
s are colimits of diagrams indexed by directed sets.
Existence of limits
A given diagram F : J → C may or may not have a limit (or colimit) in C. Indeed, there may not even be a cone to F, let alone a universal cone.A category C is said to have limits of type J if every diagram of type J has a limit in C. Specifically, a category C is said to
- have products if it has limits of type J for every small discrete category J (it need not have large products),
- have equalizers if it has limits of type
 (i.e. every parallel pair of morphisms has an equalizer),
(i.e. every parallel pair of morphisms has an equalizer), - have pullbacks if it has limits of type
 (i.e. every pair of morphisms with common codomain has a pullback).
(i.e. every pair of morphisms with common codomain has a pullback).
A complete category
Complete category
In mathematics, a complete category is a category in which all small limits exist. That is, a category C is complete if every diagram F : J → C where J is small has a limit in C. Dually, a cocomplete category is one in which all small colimits exist...
is a category that has all small limits (i.e. all limits of type J for every small category J).
One can also make the dual definitions. A category has colimits of type J if every diagram of type J has a colimit in C. A cocomplete category is one that has all small colimits.
The existence theorem for limits states that if a category C has equalizers and all products indexed by the classes Ob(J) and Hom(J), then C has all limits of type J. In this case, the limit of a diagram F : J → C can be constructed as the equalizer of the two morphisms

given (in component form) by
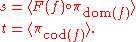
There is a dual existence theorem for colimits in terms of coequalizers and coproducts. Both of these theorems give sufficient but not necessary conditions for the existence of all (co)limits of type J.
Universal property
Limits and colimits are important special cases of universal constructions. Let C be a category and let J be a small index category. The functor categoryFunctor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
CJ may be thought of the category of all diagrams of type J in C. The diagonal functor

is the functor that maps each object N in C to the constant functor Δ(N) : J → C to N. That is, Δ(N)(X) = N for each object X in J and Δ(N)(f) = idN for each morphism f in J.
Given a diagram F: J → C (thought of as an object in CJ), a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
ψ : Δ(N) → F (which is just a morphism in the category CJ) is the same thing as a cone from N to F. The components of ψ are the morphisms ψX : N → F(X). Dually, a natural transformation ψ : F → Δ(N) is the same thing as a co-cone from F to N.
The definitions of limits and colimits can then be restated in the form:
- A limit of F is a universal morphism from Δ to F.
- A colimit of F is a universal morphism from F to Δ.
Adjunctions
Like all universal constructions, the formation of limits and colimits is functorial in nature. In other words, if every diagram of type J has a limit in C (for J small) there exists a limit functor
which assigns each diagram its limit and each natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
η : F → G the unique morphism lim η : lim F → lim G commuting with the corresponding universal cones. This functor is right adjoint to the diagonal functor Δ : C → CJ.
This adjunction gives a bijection between the set of all morphisms from N to lim F and the set of all cones from N to F

which is natural in the variables N and F. The counit of this adjunction is simply the universal cone from lim F to F. If the index category J is connected (and nonempty) then the unit of the adjunction is an isomorphism so that lim is a left inverse of Δ. This fails if J is not connected. For example, if J is a discrete category, the components of the unit are the diagonal morphisms δ : N → NJ.
Dually, if every diagram of type J has a colimit in C (for J small) there exists a colimit functor

which assigns each diagram its colimit. This functor is left adjoint to the diagonal functor Δ : C → CJ, and one has a natural isomorphism
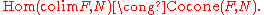
The unit of this adjunction is the universal cocone from F to colim F. If J is connected (and nonempty) then the counit is an isomorphism, so that colim is a left inverse of Δ.
Note that both the limit and the colimit functors are covariant functors.
As representations of functors
One can use Hom functorHom functor
In mathematics, specifically in category theory, hom-sets, i.e. sets of morphisms between objects, give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.-Formal...
s to relate limits and colimits in a category C to limits in Set, the category of sets
Category of sets
In the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
. This follows, in part, from the fact the covariant Hom functor Hom(N, –) : C → Set preserves all limits in C. By duality, the contravariant Hom functor must take colimits to limits.
If a diagram F : J → C has a limit in C, denoted by lim F, there is a canonical isomorphism

which is natural in the variable N. Here the functor Hom(N, F–) is the composition of the Hom functor Hom(N, –) with F. This isomorphism is the unique one which respects the limiting cones.
One can use the above relationship to define the limit of F in C. The first step is to observe that the limit of the functor Hom(N, F–) can be identified with the set of all cones from N to F:

The limiting cone is given by the family of maps πX : Cone(N, F) → Hom(N, FX) where πX(ψ) = ψX. If one is given an object L of C together with a natural isomorphism Φ : Hom(–, L) → Cone(–, F), the object L will be a limit of F with the limiting cone given by ΦL(idL). In fancy language, this amounts to saying that a limit of F is a representation
Representable functor
In mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
of the functor Cone(–, F) : C → Set.
Dually, if a diagram F : J → C has a colimit in C, denoted colim F, there is a unique canonical isomorphism
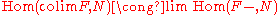
which is natural in the variable N and respects the colimiting cones. Identifying the limit of Hom(F–, N) with the set Cocone(F, N), this relationship can be used to define the colimit of the diagram F as a representation of the functor Cocone(F, –).
Interchange of limits and colimits of sets
Let I be a finite category and J be a small filtered categoryFiltered category
In category theory, filtered categories generalize the notion of directed set understood as a category .A category J is filtered when...
. For any bifunctor
- F : I × J → Set
there is a natural isomorphism

In words, filtered colimits in Set commute with finite limits.
Functors and limits
If F : J → C is a diagram in C and G : C → D is a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
then by composition (recall that a diagram is just a functor) one obtains a diagram GF : J → D. A natural question is then:
- “How are the limits of GF related to those of F?”
Preservation of limits
A functor G : C → D induces a map from Cone(F) to Cone(GF): if Ψ is a cone from N to F then GΨ is a cone from GN to GF. The functor G is said to preserve the limits of F if (GL, Gφ) is a limit of GF whenever (L, φ) is a limit of F. (Note that if the limit of F does not exist, then G vacuouslyVacuous truth
A vacuous truth is a truth that is devoid of content because it asserts something about all members of a class that is empty or because it says "If A then B" when in fact A is inherently false. For example, the statement "all cell phones in the room are turned off" may be true...
preserves the limits of F.)
A functor G is said to preserve all limits of type J if it preserves the limits of all diagrams F : J → C. For example, one can say that G preserves products, equalizers, pullbacks, etc. A continuous functor is one that preserves all small limits.
One can make analogous definitions for colimits. For instance, a functor G preserves the colimits of F if G(L, φ) is a colimit of GF whenever (L, φ) is a colimit of F. A cocontinuous functor is one that preserves all small colimits.
If C is a complete category
Complete category
In mathematics, a complete category is a category in which all small limits exist. That is, a category C is complete if every diagram F : J → C where J is small has a limit in C. Dually, a cocomplete category is one in which all small colimits exist...
, then, by the above existence theorem for limits, a functor G : C → D is continuous if and only if it preserves (small) products and equalizers. Dually, G is cocontinuous if and only if it preserves (small) coproducts and coequalizers.
An important property of adjoint functors
Adjoint functors
In mathematics, adjoint functors are pairs of functors which stand in a particular relationship with one another, called an adjunction. The relationship of adjunction is ubiquitous in mathematics, as it rigorously reflects the intuitive notions of optimization and efficiency...
is that every right adjoint functor is continuous and every left adjoint functor is cocontinuous. Since adjoint functors exist in abundance, this gives numerous examples of continuous and cocontinuous functors.
For a given diagram F : J → C and functor G : C → D, if both F and GF have specified limits there is a unique canonical morphism
- τF : G lim F → lim GF
which respects the corresponding limit cones. The functor G preserves the limits of F if and only this map is an isomorphism. If the categories C and D have all limits of type J then lim is a functor and the morphisms τF form the components of a natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
- τ : G lim → lim GJ.
The functor G preserves all limits of type J if and only if τ is a natural isomorphism. In this sense, the functor G can be said to commute with limits (up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
a canonical natural isomorphism).
Preservation of limits and colimits is a concept that only applies to covariant functors. For contravariant functors the corresponding notions would be a functor that takes colimits to limits, or one that takes limits to colimits.
Lifting of limits
A functor G : C → D is said to lift limits for a diagram F : J → C if whenever (L, φ) is a limit of GF there exists a limit (L′, φ′) of F such that G(L′, φ′) = (L, φ). A functor G lifts limits of type J if it lifts limits for all diagrams of type J. One can therefore talk about lifting products, equalizers, pullbacks, etc. Finally, one says that G lifts limits if it lifts all limits. There are dual definitions for the lifting of colimits.A functor G lifts limits uniquely for a diagram F if there is a unique preimage cone (L′, φ′) such that (L′, φ′) is a limit of F and G(L′, φ′) = (L, φ). One can show that G lifts limits uniquely if and only if it lifts limits and is amnestic
Amnestic functor
In the mathematical field of category theory, an amnestic functor F : A → B is a functor for which A-isomorphism ƒ is an identity whenever Fƒ is an identity.- References :...
.
Lifting of limits is clearly related to preservation of limits. If G lifts limits for a diagram F and GF has a limit, then F also has a limit and G preserves the limits of F. It follows that:
- If G lifts limits of all type J and D has all limits of type J, then C also has all limits of type J and G preserves these limits.
- If G lifts all small limits and D is complete, then C is also complete and G is continuous.
The dual statements for colimits are equally valid.
Creation and reflection of limits
Let F : J → C be a diagram. A functor G : C → D is said to- create limits for F if whenever (L, φ) is a limit of GF there exists a unique cone (L′, φ′) to F such that G(L′, φ′) = (L, φ), and furthermore, this cone is a limit of F.
- reflect limits for F if each cone to F whose image under G is a limit of GF is already a limit of F.
Dually, one can define creation and reflection of colimits.
The following statements are easily seen to be equivalent:
- The functor G creates limits.
- The functor G lifts limits uniquely and reflects limits.
There are examples of functors which lift limits uniquely but neither create nor reflect them.
Examples
- For any category C and object A of C the Hom functorHom functorIn mathematics, specifically in category theory, hom-sets, i.e. sets of morphisms between objects, give rise to important functors to the category of sets. These functors are called hom-functors and have numerous applications in category theory and other branches of mathematics.-Formal...
Hom(A,–) : C → Set preserves all limits in C. In particular, Hom functors are continuous. Hom functors need not preserve colimits. - Every representable functorRepresentable functorIn mathematics, particularly category theory, a representable functor is a functor of a special form from an arbitrary category into the category of sets. Such functors give representations of an abstract category in terms of known structures In mathematics, particularly category theory, a...
C → Set preserves limits (but not necessarily colimits). - The forgetful functorForgetful functorIn mathematics, in the area of category theory, a forgetful functor is a type of functor. The nomenclature is suggestive of such a functor's behaviour: given some object with structure as input, some or all of the object's structure or properties is 'forgotten' in the output...
U : Grp → Set creates (and preserves) all small limits and filtered colimits; however, U does not preserve coproducts. This situation is typical of algebraic forgetful functors. - The free functor F : Set → Grp (which assigns to every set S the free groupFree groupIn mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
over S) is left adjoint to forgetful functor U and is, therefore, cocontinuous. This explains why the free productFree productIn mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
of two free groups G and H is the free group generated by the disjoint unionDisjoint unionIn mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of the generators of G and H. - The inclusion functor Ab → Grp creates limits but does not preserve coproducts (the coproduct of two abelian groups being the direct sum).
- The forgetful functor Top → Set lifts limits and colimits uniquely but creates neither.
- Let Metc be the category of metric spaceMetric spaceIn mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
s with continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s for morphisms. The forgetful functor Metc → Set lifts finite limits but does not lift them uniquely.
A note on terminology
Older terminology referred to limits as "inverse limits" or "projective limits," and to colimits as "direct limits" or "inductive limits." This has been the source of a lot of confusion.There are several ways to remember the modern terminology. First of all,
- cokernels,
- coequalizers, and
- codomains
are types of colimits, whereas
- kernels,
- equalizers, and
- domains
are types of limits. Second, the prefix "co" implies "first variable of the
 ". Terms like "cohomology" and "cofibration" all have a slightly stronger association with the first variable, i.e., the contravariant variable, of the
". Terms like "cohomology" and "cofibration" all have a slightly stronger association with the first variable, i.e., the contravariant variable, of the  bifunctor.
bifunctor.External links
- Interactive Web page which generates examples of limits and colimits in the category of finite sets. Written by Jocelyn Paine.

