Zero morphism
Encyclopedia
In category theory
, a zero morphism is a special kind of morphism
exhibiting properties like those to and from a zero object.
Suppose C is a category
, and f : X → Y is a morphism in C. The morphism f is called a constant morphism (or sometimes left zero morphism) if for any object W in C and any g, h : W → X, fg = fh. Dually, f is called a coconstant morphism (or sometimes right zero morphism) if for any object Z in C and any g, h ∈ MorC(Y, Z), gf = hf. A zero morphism is one that is both a constant morphism and a coconstant morphism.
If C has a zero object 0, given two objects X and Y in C, there are canonical morphisms f : 0 → X and g : Y → 0. Then, fg is a zero morphism in MorC(Y, X).
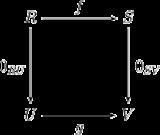
A category with zero morphisms is one where, for any two objects A and B in C, there is a fixed morphism 0AB : A → B such that for all objects X, Y, Z in C and all morphisms f : Y → Z, g : X → Y, the following diagram commutes:
The morphisms 0XY are forced to be zero morphisms and form a compatible system of such. If C is a category with zero morphisms, then the collection of 0XY is unique. A category with a zero object is a category with zero morphisms (given by the composition 0XY : X → 0 → Y described above).
If a category has zero morphisms, then one can define the notions of kernel
and cokernel
for any morphism in that category.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a zero morphism is a special kind of morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
exhibiting properties like those to and from a zero object.
Suppose C is a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
, and f : X → Y is a morphism in C. The morphism f is called a constant morphism (or sometimes left zero morphism) if for any object W in C and any g, h : W → X, fg = fh. Dually, f is called a coconstant morphism (or sometimes right zero morphism) if for any object Z in C and any g, h ∈ MorC(Y, Z), gf = hf. A zero morphism is one that is both a constant morphism and a coconstant morphism.
If C has a zero object 0, given two objects X and Y in C, there are canonical morphisms f : 0 → X and g : Y → 0. Then, fg is a zero morphism in MorC(Y, X).
A category with zero morphisms is one where, for any two objects A and B in C, there is a fixed morphism 0AB : A → B such that for all objects X, Y, Z in C and all morphisms f : Y → Z, g : X → Y, the following diagram commutes:
The morphisms 0XY are forced to be zero morphisms and form a compatible system of such. If C is a category with zero morphisms, then the collection of 0XY is unique. A category with a zero object is a category with zero morphisms (given by the composition 0XY : X → 0 → Y described above).
If a category has zero morphisms, then one can define the notions of kernel
Kernel (category theory)
In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
and cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
for any morphism in that category.
Examples
- In the category of groupsCategory of groupsIn mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
(or of modulesModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
), a zero morphism is a homomorphismHomomorphismIn abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
f : G → H that maps all of G to the identity elementIdentity elementIn mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
of H. The null object in the category of groups is the trivial groupTrivial groupIn mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
1 = {1}, which is unique up to isomorphism. Every zero morphism can be factored through 1, i. e., f : G → 1 → H.
- More generally, suppose C is any category with a zero object 0. Then for all objects X and Y there is a unique sequence of morphisms
-
- 0XY : X → 0 → Y
- The family of all morphisms so constructed endows C with the structure of a category with zero morphisms.
- If C is a preadditive categoryPreadditive categoryIn mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
, then every morphism set Mor(X,Y) is an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
and therefore has a zero element. These zero elements form a compatible family of zero morphisms for C making it into a category with zero morphisms.
- The category SetCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
(sets with functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s as morphisms) does not have a zero object, but it does have an initial objectInitial objectIn category theory, an abstract branch of mathematics, an initial object of a category C is an object I in C such that for every object X in C, there exists precisely one morphism I → X...
, the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
∅. The only zero morphisms in Set are the functions ∅ → X for a set X.

