Indexed family
Encyclopedia
In mathematics
, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers.
Formally, an indexed family is the same thing as a function
. A function with domain J and codomain X is equivalent to a family of elements of X indexed by elements of J. The only difference is that indexed families are thought of as collections instead of as functions. A value is considered to be an element of a family whenever it is an element of the image of the family's underlying function.
When a function f : J → X is treated as a family, J is called the index set
of the family, the functional image f(j) for j ∈ J is denoted xj, and the mapping f is denoted {xj}j∈J or simply {xj}.
Next, if the set X is the power set of a set U, then the family {xj}j∈J is called a family of sets indexed by J .
. An indexed family is denoted by 
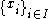, where it is understood that there is a function x that maps i to 
.
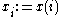An indexed family can be turned into a set by considering the set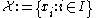
, that is, the range of x, but this will collapse the elements 
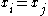with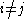 
into elements in 
.
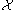Definition. Let S be a set. An indexed family of sets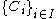
is an indexed family that maps I to elements of the power set of S.
Hence, an indexed family of sets is conceptually different from a family of sets (which is just a synonym for "set of sets"), but in practice the distinction is sometimes fuzzy and the indexed family is identified with its range and treated like an ordinary family.
is used the indexed objects form a family. For example, consider the following sentence.
Here (vi)i ∈ {1, …, n} denotes a family of vectors. The i-th vector vi only makes sense with respect to this family, as sets are unordered and there is no i-th vector of a set. Furthermore, linear independence
is only defined as the property of a collection; it therefore is important if those vectors are linearly independent as a set or as a family.
If we consider n = 2 and v1 = v2 = (1, 0), the set of them consists of only one element and is linearly independent, but the family contains the same element twice and is linearly dependent.
As in the previous example it is important that the rows of A are linearly independent as a family, not as a set. For, consider the matrix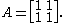
The set of rows only consists of a single element (1, 1) and is linearly independent, but the matrix is not invertible. The family of rows contains two elements and is linearly dependent. The statement is therefore correct if it refers to the family of rows, but wrong if it refers to the set of rows.
and families are formally equivalent, as any function f with domain
I induces a family (f(i))i∈I. In practice, however, a family is viewed as a collection, not as a function: being an element of a family is equivalent with being in the range of the corresponding function. A family contains any element exactly once, if and only if
the corresponding function is injective.
Like a set, a family is a container and any set X gives rise to a family (x)x∈X. Thus any set naturally becomes a family. For any family (Ai)i∈I there is the set of all elements {Ai | i∈I}, but this does not carry any information on multiple containment or the structure of I. Hence, by using a set instead of the family, some information might be lost.
.
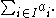
When (Ai)i∈I is a family of sets
, the union
of all those sets is denoted by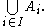
Likewise for intersection
s and cartesian product
s.
J is a subset of I and for all i in J
is called a diagram
. A diagram is a functor
giving rise to an indexed family of objects in a category
C, indexed by another category J, and related by morphism
s depending on two indices.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an indexed family is a collection of values that are associated with indexes. For example, a family of real numbers, indexed by the integers is a collection of real numbers, where each integer is associated with one of the real numbers.
Formally, an indexed family is the same thing as a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. A function with domain J and codomain X is equivalent to a family of elements of X indexed by elements of J. The only difference is that indexed families are thought of as collections instead of as functions. A value is considered to be an element of a family whenever it is an element of the image of the family's underlying function.
When a function f : J → X is treated as a family, J is called the index set
Index set
In mathematics, the elements of a set A may be indexed or labeled by means of a set J that is on that account called an index set...
of the family, the functional image f(j) for j ∈ J is denoted xj, and the mapping f is denoted {xj}j∈J or simply {xj}.
Next, if the set X is the power set of a set U, then the family {xj}j∈J is called a family of sets indexed by J .
Mathematical statement
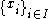Definition. Let X and I be any sets. Then by family of elements in X indexed by I , we mean a function. An indexed family is denoted by , where it is understood that there is a function x that maps i to 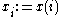.An indexed family can be turned into a set by considering the set
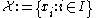, that is, the range of x, but this will collapse the elements 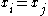with 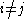into elements in 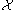.Definition. Let S be a set. An indexed family of sets
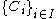is an indexed family that maps I to elements of the power set of S.Hence, an indexed family of sets is conceptually different from a family of sets (which is just a synonym for "set of sets"), but in practice the distinction is sometimes fuzzy and the indexed family is identified with its range and treated like an ordinary family.
Index notation
Whenever index notationIndex notation
Index notation is used in mathematics and computer programming to specify the elements of matrices or the components of a vector. The formalism of how indices are used varies according to the discipline...
is used the indexed objects form a family. For example, consider the following sentence.
- The vectors v1, …, vn are linearly independent.
Here (vi)i ∈ {1, …, n} denotes a family of vectors. The i-th vector vi only makes sense with respect to this family, as sets are unordered and there is no i-th vector of a set. Furthermore, linear independence
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
is only defined as the property of a collection; it therefore is important if those vectors are linearly independent as a set or as a family.
If we consider n = 2 and v1 = v2 = (1, 0), the set of them consists of only one element and is linearly independent, but the family contains the same element twice and is linearly dependent.
Matrices
Suppose a text states the following:- A square matrix A is invertible, if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the rows of A are linearly independent.
As in the previous example it is important that the rows of A are linearly independent as a family, not as a set. For, consider the matrix
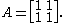
The set of rows only consists of a single element (1, 1) and is linearly independent, but the matrix is not invertible. The family of rows contains two elements and is linearly dependent. The statement is therefore correct if it refers to the family of rows, but wrong if it refers to the set of rows.
Functions, sets and families
Surjective functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
and families are formally equivalent, as any function f with domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
I induces a family (f(i))i∈I. In practice, however, a family is viewed as a collection, not as a function: being an element of a family is equivalent with being in the range of the corresponding function. A family contains any element exactly once, if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the corresponding function is injective.
Like a set, a family is a container and any set X gives rise to a family (x)x∈X. Thus any set naturally becomes a family. For any family (Ai)i∈I there is the set of all elements {Ai | i∈I}, but this does not carry any information on multiple containment or the structure of I. Hence, by using a set instead of the family, some information might be lost.
Examples
Let n be the finite set {1, 2, …, n}, where n is a positive integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
.
- An ordered pairOrdered pairIn mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
is a family indexed by the two element set 2 = {1, 2}. - An n-tupleTupleIn mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
is a family indexed by n. - An infinite sequenceSequenceIn mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
is a family indexed by the natural numbers. - A listTupleIn mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
is an n-tuple for an unspecified n, or an infinite sequence. - An n×m matrixMatrix (mathematics)In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
is a family indexed by the cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
n×m. - A netNet (mathematics)In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
is a family indexed by a directed setDirected setIn mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
.
Operations on families
Index sets are often used in sums and other similar operations. For example, if (ai)i∈I is a family of numbers, the sum of all those numbers is denoted by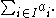When (Ai)i∈I is a family of sets
Family of sets
In set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
, the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of all those sets is denoted by
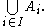
Likewise for intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
s and cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
s.
Subfamily
A family (Bi)i∈J is a subfamily of a family (Ai)i∈I, if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
J is a subset of I and for all i in J
- Bi = Ai
Usage in category theory
The analogous concept in category theoryCategory theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
is called a diagram
Diagram (category theory)
In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function...
. A diagram is a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
giving rise to an indexed family of objects in a category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
C, indexed by another category J, and related by morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s depending on two indices.
See also
- CoproductCoproductIn category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
- Disjoint unionDisjoint unionIn mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
- Tagged unionTagged unionIn computer science, a tagged union, also called a variant, variant record, discriminated union, or disjoint union, is a data structure used to hold a value that could take on several different, but fixed types. Only one of the types can be in use at any one time, and a tag field explicitly...
- Index notationIndex notationIndex notation is used in mathematics and computer programming to specify the elements of matrices or the components of a vector. The formalism of how indices are used varies according to the discipline...
- ArrayArrayIn computer science, an array data structure or simply array is a data structure consisting of a collection of elements , each identified by at least one index...
- Net (mathematics)Net (mathematics)In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
- Diagram (category theory)Diagram (category theory)In category theory, a branch of mathematics, a diagram is the categorical analogue of an indexed family in set theory. The primary difference is that in the categorical setting one has morphisms. An indexed family of sets is a collection of sets, indexed by a fixed set; equivalently, a function...
- Parametric familyParametric familyIn mathematics and its applications, a parametric family or a parameterized family is a family of objects whose definitions depend on a set of parameters....