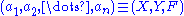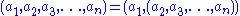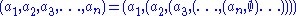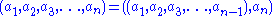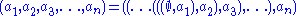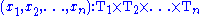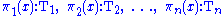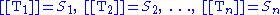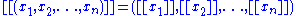Tuple
Encyclopedia
In mathematics
and computer science
, a tuple is an ordered list of elements. In set theory
, an (ordered) -tuple is a sequence
-tuple is a sequence
(or ordered list) of elements, where
elements, where  is a positive integer. There is also one
is a positive integer. There is also one  -tuple, an empty sequence. An
-tuple, an empty sequence. An  -tuple is defined inductively
-tuple is defined inductively
using the construction of an ordered pair
. Tuples are usually written by listing the elements within parentheses " " and separated by commas; for example,
" and separated by commas; for example, 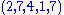 denotes a
denotes a 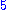 -tuple. Sometimes other delimiters are used, such as square brackets "
-tuple. Sometimes other delimiters are used, such as square brackets " " or angle brackets "
" or angle brackets " ". Braces "" are almost never used for tuples, as they are the standard notation for sets.
". Braces "" are almost never used for tuples, as they are the standard notation for sets.
Tuples are often used to describe other mathematical objects, such as vectors
. In algebra
, a ring
is commonly defined as a 3-tuple , where
, where  is some set, and "
is some set, and " ", and "
", and " " are functions
" are functions
mapping the Cartesian product
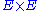 to
to  with specific properties. In computer science, tuples are directly implemented as product types in most functional programming languages. More commonly, they are implemented as record types
with specific properties. In computer science, tuples are directly implemented as product types in most functional programming languages. More commonly, they are implemented as record types
, where the components are labeled instead of being identified by position alone. This approach is also used in relational algebra
.
 ‑tuple, ..., where the prefixes are taken from the Latin
‑tuple, ..., where the prefixes are taken from the Latin
names of the numerals. The unique ‑tuple is called the null tuple. A
‑tuple is called the null tuple. A 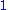 ‑tuple is called a singleton, a
‑tuple is called a singleton, a 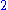 ‑tuple is called a pair and a
‑tuple is called a pair and a 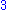 ‑tuple is a triple or triplet. The
‑tuple is a triple or triplet. The  can be any nonnegative integer. For example, a complex number
can be any nonnegative integer. For example, a complex number
can be represented as a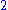 ‑tuple, a quaternion
‑tuple, a quaternion
can be represented as a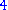 ‑tuple, an octonion
‑tuple, an octonion
can be represented as an octuple, (many mathematicians write the abbreviation "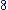 ‑tuple") and a sedenion
‑tuple") and a sedenion
can be represented as a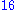 ‑tuple.
‑tuple.
Although these uses treat ‑tuple as the suffix, the original suffix was ‑ple as in "triple" (three-fold) or "decuple" (ten‑fold). This originates from a medieval Latin suffix ‑plus (meaning "more") related to Greek ‑πλοῦς, which replaced the classical and late antique ‑plex (meaning "folded").
 -tuples is
-tuples is
Thus a tuple has properties that distinguish it from a set.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, a tuple is an ordered list of elements. In set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, an (ordered)
 -tuple is a sequence
-tuple is a sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
(or ordered list) of
 elements, where
elements, where  is a positive integer. There is also one
is a positive integer. There is also one  -tuple, an empty sequence. An
-tuple, an empty sequence. An  -tuple is defined inductively
-tuple is defined inductivelyRecursive definition
In mathematical logic and computer science, a recursive definition is used to define an object in terms of itself ....
using the construction of an ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
. Tuples are usually written by listing the elements within parentheses "
 " and separated by commas; for example,
" and separated by commas; for example, 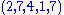 denotes a
denotes a 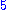 -tuple. Sometimes other delimiters are used, such as square brackets "
-tuple. Sometimes other delimiters are used, such as square brackets " " or angle brackets "
" or angle brackets " ". Braces "" are almost never used for tuples, as they are the standard notation for sets.
". Braces "" are almost never used for tuples, as they are the standard notation for sets.Tuples are often used to describe other mathematical objects, such as vectors
Vector (mathematics and physics)
In mathematics and physics, a vector is an element of a vector space. If n is a non negative integer and K is either the field of the real numbers or the field of the complex number, then K^n is naturally endowed with a structure of vector space, where K^n is the set of the ordered sequences of n...
. In algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
is commonly defined as a 3-tuple
 , where
, where  is some set, and "
is some set, and " ", and "
", and " " are functions
" are functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
mapping the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
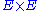 to
to  with specific properties. In computer science, tuples are directly implemented as product types in most functional programming languages. More commonly, they are implemented as record types
with specific properties. In computer science, tuples are directly implemented as product types in most functional programming languages. More commonly, they are implemented as record typesRecord (computer science)
In computer science, a record is an instance of a product of primitive data types called a tuple. In C it is the compound data in a struct. Records are among the simplest data structures. A record is a value that contains other values, typically in fixed number and sequence and typically indexed...
, where the components are labeled instead of being identified by position alone. This approach is also used in relational algebra
Relational algebra
Relational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
.
Etymology
The term originated as an abstraction of the sequence: single, double, triple, quadruple, quintuple, sextuple, septuple, octuple, ..., ‑tuple, ..., where the prefixes are taken from the Latin
‑tuple, ..., where the prefixes are taken from the LatinLatin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
names of the numerals. The unique
 ‑tuple is called the null tuple. A
‑tuple is called the null tuple. A 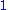 ‑tuple is called a singleton, a
‑tuple is called a singleton, a 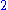 ‑tuple is called a pair and a
‑tuple is called a pair and a 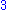 ‑tuple is a triple or triplet. The
‑tuple is a triple or triplet. The  can be any nonnegative integer. For example, a complex number
can be any nonnegative integer. For example, a complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
can be represented as a
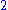 ‑tuple, a quaternion
‑tuple, a quaternionQuaternion
In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...
can be represented as a
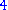 ‑tuple, an octonion
‑tuple, an octonionOctonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
can be represented as an octuple, (many mathematicians write the abbreviation "
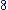 ‑tuple") and a sedenion
‑tuple") and a sedenionSedenion
In abstract algebra, sedenions form a 16-dimensional non-associative algebra over the reals obtained by applying the Cayley–Dickson construction to the octonions...
can be represented as a
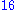 ‑tuple.
‑tuple.Although these uses treat ‑tuple as the suffix, the original suffix was ‑ple as in "triple" (three-fold) or "decuple" (ten‑fold). This originates from a medieval Latin suffix ‑plus (meaning "more") related to Greek ‑πλοῦς, which replaced the classical and late antique ‑plex (meaning "folded").
Characteristic properties
The general rule for the identity of two -tuples is
-tuples is
-
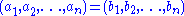 if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
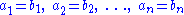
Thus a tuple has properties that distinguish it from a set.
- A tuple may contain multiple instances of the same element, so tuple
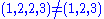 ; but multisetMultisetIn mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
; but multisetMultisetIn mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
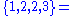 set
set 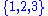 .
.
- Tuple elements are ordered: tuple
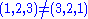 , but set
, but set 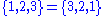 .
. - A tuple has a finite number of elements, while a set or a multiset may have an infinite number of elements.
Tuples as functions
An -tuple can also be regarded as a function, F, whose domain is the tuple's implicit set of element indices, X, and whose codomain, Y, is the tuple's set of elements. Formally:
-tuple can also be regarded as a function, F, whose domain is the tuple's implicit set of element indices, X, and whose codomain, Y, is the tuple's set of elements. Formally:
where:-
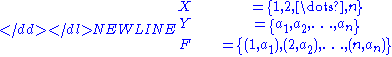
Tuples as nested ordered pairs
Another way of formalizing tuples is as nested ordered pairOrdered pairIn mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
s:- The
 -tuple (i.e. the empty tuple) is represented by the empty set
-tuple (i.e. the empty tuple) is represented by the empty set  .
. - An
 -tuple, with
-tuple, with  , can be defined as an ordered pairOrdered pairIn mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
, can be defined as an ordered pairOrdered pairIn mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
of its first entry and an -tuple (which contains the remaining entries when
-tuple (which contains the remaining entries when  ):
):
-
This definition can be applied recursively to the -tuple:
-tuple:
Thus, for example:-
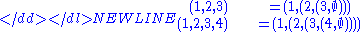
A variant of this definition starts "peeling off" elements from the other end:- The
 -tuple is the empty set
-tuple is the empty set  .
. - For
 :
:
-
This definition can be applied recursively:
Thus, for example:-
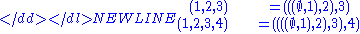
Tuples as nested sets
Using Kuratowski's representation for an ordered pair, the second definition above can be reformulated in terms of pure set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
:- The
 -tuple (i.e. the empty tuple) is represented by the empty set
-tuple (i.e. the empty tuple) is represented by the empty set  ;
; - Let
 be an
be an  -tuple
-tuple 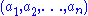 , and let
, and let 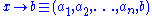 . Then,
. Then, 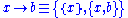 . (The right arrow,
. (The right arrow,  , could be read as "adjoined with".)
, could be read as "adjoined with".)
In this formulation:-
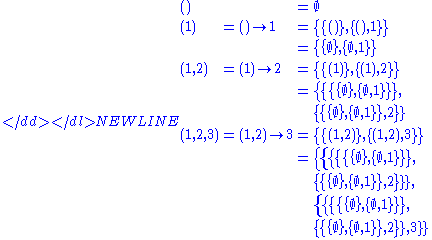
Relational model
In database theoryDatabase theoryDatabase theory encapsulates a broad range of topics related to the study and research of the theoretical realm of databases and database management systems....
, the relational modelRelational modelThe relational model for database management is a database model based on first-order predicate logic, first formulated and proposed in 1969 by Edgar F...
uses a tuple definition similar to tuples as functions, but each tuple element is identified by a distinct name, called an attribute, instead of a number; this leads to a more user-friendly and practical notation, A tuple in the relational model is formally defined as a finite functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that maps attributes to values. For example:- (player : "Harry", score : 25)
In this notation, attribute–value pairs may appear in any order. The distinction between tuples in the relational model and those in set theory is only superficial; the above example can be interpreted as a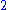 -tuple if an arbitrary total orderTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
-tuple if an arbitrary total orderTotal orderIn set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
is imposed on the attributes (e.g.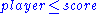 ) and then the elements are distinguished by this ordering rather than by the attributes themselves. Conversely, a
) and then the elements are distinguished by this ordering rather than by the attributes themselves. Conversely, a 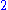 -tuple may be interpreted as relational model tuple over the attributes
-tuple may be interpreted as relational model tuple over the attributes 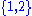 .
.
In the relational model, a relationRelation (database)In relational model:A relation value, which is assigned to a certain relation variable, is time-varying. By using a Data Definition Language , it is able to define relation variables.The following is an example of a heading which consists of three attributes....
is a (possibly empty) finite set of tuples all having the same finite set of attributes. This set of attributes is more formally called the sort of the relation, or more casually referred to as the set of column namesColumn (database)In the context of a relational database table, a column is a set of data values of a particular simple type, one for each row of the table. The columns provide the structure according to which the rows are composed....
. A tuple is usually implemented as a rowRow (database)In the context of a relational database, a row—also called a record or tuple—represents a single, implicitly structured data item in a table. In simple terms, a database table can be thought of as consisting of rows and columns or fields...
in a database table, but see relational algebraRelational algebraRelational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
for means of deriving tuples not physically represented in a table.
Type theory
In type theoryType theoryIn mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
, commonly used in programming languageProgramming languageA programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s, a tuple has a product typeProduct typeIn programming languages and type theory, a product of types is another, compounded, type in a structure. The "operands" of the product are types, and the structure of a product type is determined by the fixed order of the operands in the product. An instance of a product type retains the fixed...
; this fixes not only the length, but also the underlying types of each component. Formally:
and the projectionProjection (mathematics)Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
s are term constructors:
The tuple with labeled elements used in the relational model has a record type. Both of these types can be defined as simple extensions of the simply typed lambda calculusSimply typed lambda calculusThe simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...
.
The notion of a tuple in type theory and that in set theory are related in the following way: If we consider the natural modelModel theoryIn mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of a type theory, and use the Scott brackets to indicate the semantic interpretation, then the model consists of some sets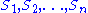 (note: the use of italics here that distinguishes sets from types) such that:
(note: the use of italics here that distinguishes sets from types) such that:
and the interpretation of the basic terms is:-
 .
.
The -tuple of type theory has the natural interpretation as an
-tuple of type theory has the natural interpretation as an  -tuple of set theory:
-tuple of set theory:
The unit typeUnit typeIn the area of mathematical logic, and computer science known as type theory, a unit type is a type that allows only one value . The carrier associated with a unit type can be any singleton set. There is an isomorphism between any two such sets, so it is customary to talk about the unit type and...
has as semantic interpretation the -tuple.
-tuple.
See also
- ArityArityIn logic, mathematics, and computer science, the arity of a function or operation is the number of arguments or operands that the function takes. The arity of a relation is the dimension of the domain in the corresponding Cartesian product...
- Exponential objectExponential objectIn mathematics, specifically in category theory, an exponential object is the categorical equivalent of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories...
- Formal languageFormal languageA formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
- OLAP: Multidimensional Expressions
- Relation (mathematics)Relation (mathematics)In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
- Tuplespace
External links
- The
- The
- The
- Tuple elements are ordered: tuple