Set theory - AbsoluteAstronomy.com

Set theory is the branch of mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics. The language of set theory can be used in the definitions of nearly all mathematical objects.

The modern study of set theory was initiated by Georg Cantor

Georg Cantor

Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...

and Richard Dedekind

Richard Dedekind

Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...

in the 1870s. After the discovery of paradoxes

Paradoxes of set theory

This article contains a discussion of paradoxes of set theory. As with most mathematical paradoxes, they generally reveal surprising and counter-intuitive mathematical results, rather than actual logical contradictions within modern axiomatic set theory....

in naive set theory

Naive set theory

Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...

, numerous axiom systems

Axiomatic system

In mathematics, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A mathematical theory consists of an axiomatic system and all its derived theorems...

were proposed in the early twentieth century, of which the Zermelo–Fraenkel axioms

Zermelo–Fraenkel set theory

In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...

, with the axiom of choice, are the best-known.

Set theory is commonly employed as a foundational system for mathematics, particularly in the form of Zermelo–Fraenkel set theory

Zermelo–Fraenkel set theory

with the axiom of choice. Beyond its foundational role, set theory is a branch of mathematics

Mathematics

in its own right, with an active research community. Contemporary research into set theory includes a diverse collection of topics, ranging from the structure of the real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

line to the study of the consistency

Consistency

Consistency can refer to:* Consistency , the psychological need to be consistent with prior acts and statements* "Consistency", an 1887 speech by Mark Twain...

of large cardinals.

History

Mathematical topics typically emerge and evolve through interactions among many researchers. Set theory, however, was founded by a single paper in 1874 by Georg Cantor

Georg Cantor

: "On a Characteristic Property of All Real Algebraic Numbers".

Since the 5th century BC, beginning with Greek

Greek mathematics

Greek mathematics, as that term is used in this article, is the mathematics written in Greek, developed from the 7th century BC to the 4th century AD around the Eastern shores of the Mediterranean. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to...

mathematician Zeno of Elea

Zeno of Elea

Zeno of Elea was a pre-Socratic Greek philosopher of southern Italy and a member of the Eleatic School founded by Parmenides. Aristotle called him the inventor of the dialectic. He is best known for his paradoxes, which Bertrand Russell has described as "immeasurably subtle and profound".- Life...

in the West and early Indian mathematicians

Indian mathematics

Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics , important contributions were made by scholars like Aryabhata, Brahmagupta, and Bhaskara II. The decimal number system in use today was first...

in the East, mathematicians had struggled with the concept of infinity

Infinity

Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...

. Especially notable is the work of Bernard Bolzano

Bernard Bolzano

Bernhard Placidus Johann Nepomuk Bolzano , Bernard Bolzano in English, was a Bohemian mathematician, logician, philosopher, theologian, Catholic priest and antimilitarist of German mother tongue.-Family:Bolzano was the son of two pious Catholics...

in the first half of the 19th century. The modern understanding of infinity began in 1867-71, with Cantor's work on number theory. An 1872 meeting between Cantor and Richard Dedekind

Richard Dedekind

Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...

influenced Cantor's thinking and culminated in Cantor's 1874 paper.

Cantor's work initially polarized the mathematicians of his day. While Karl Weierstrass

Karl Weierstrass

Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....

and Dedekind supported Cantor, Leopold Kronecker

Leopold Kronecker

Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...

, now seen as a founder of mathematical constructivism, did not. Cantorian set theory eventually became widespread, due to the utility of Cantorian concepts, such as one-to-one correspondence among sets, his proof that there are more real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s than integers, and the "infinity of infinities" ("Cantor's paradise") resulting from the power set operation. This utility of set theory led to the article "Mengenlehre" contributed in 1898 by Arthur Schoenflies to Klein's encyclopedia

Klein's encyclopedia

In mathematics, Klein’s encyclopedia refers to a German mathematical encyclopedia published in six volumes from 1898 to 1933. Felix Klein and Wilhelm Meyer were organizers of the encyclopedia. Its title in English is "Encyclopedia of mathematical sciences including their applications", which is...

.

The next wave of excitement in set theory came around 1900, when it was discovered that Cantorian set theory gave rise to several contradictions, called antinomies or paradox

Paradox

Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...

es. Bertrand Russell

Bertrand Russell

Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...

and Ernst Zermelo

Ernst Zermelo

Ernst Friedrich Ferdinand Zermelo was a German mathematician, whose work has major implications for the foundations of mathematics and hence on philosophy. He is known for his role in developing Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem.-Life:He graduated...

independently found the simplest and best known paradox, now called Russell's paradox

Russell's paradox

In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...

: consider "the set of all sets that are not members of themselves", which leads to a contradiction since it must be a member of itself, and not a member of itself. In 1899 Cantor had himself posed the question "What is the cardinal number

Cardinal number

In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...

of the set of all sets?", and obtained a related paradox. Russell used his paradox as a theme in his 1903 review of continental mathematics in his Principles of Mathematics.

The momentum of set theory was such that debate on the paradoxes did not lead to its abandonment. The work of Zermelo in 1908 and Abraham Fraenkel in 1922 resulted in the canonical axiomatic set theory ZFC, which is thought to be free of paradoxes. The work of analysts

Real analysis

Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...

such as Henri Lebesgue

Henri Lebesgue

Henri Léon Lebesgue was a French mathematician most famous for his theory of integration, which was a generalization of the seventeenth century concept of integration—summing the area between an axis and the curve of a function defined for that axis...

demonstrated the great mathematical utility of set theory. Axiomatic set theory has become woven into the fabric of modern mathematics.

Basic concepts

Set theory begins with a fundamental binary relation

Binary relation

In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...

between an object and a set . If is a member (or element) of , write . Since sets are objects, the membership relation can relate sets as well.

A derived binary relation

Binary relation

between two sets is the subset relation, also called set inclusion. If all the members of set are also members of set , then is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

of , denoted . For example, is a subset of , but is not. From this definition, it is clear that a set is a subset of itself; in cases where one wishes to avoid this, the term proper subset is defined to exclude this possibility.

Just as arithmetic

Arithmetic

Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...

features binary operation

Binary operation

In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....

s on number

Number

A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....

s, set theory features binary operations on sets. The:

Union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...

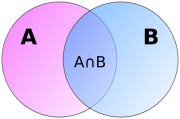
of the sets and , denoted , is the set of all objects that are a member of , or , or both. The union of and is the set .
Intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....

of the sets and , denoted , is the set of all objects that are members of both and . The intersection of and is the set .
Set difference of and , denoted is the set of all members of that are not members of . The set difference is , while, conversely, the set difference is . When is a subset of , the set difference is also called the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...

of in . In this case, if the choice of is clear from the context, the notation is sometimes used instead of , particularly if is a universal set
Universal set
In set theory, a universal set is a set which contains all objects, including itself. In set theory as usually formulated, the conception of a set of all sets leads to a paradox...

as in the study of Venn diagram
Venn diagram
Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...

s.
Symmetric difference
Symmetric difference
In mathematics, the symmetric difference of two sets is the set of elements which are in either of the sets and not in their intersection. The symmetric difference of the sets A and B is commonly denoted by A\,\Delta\,B\,orA \ominus B....

of sets and is the set of all objects that are a member of exactly one of and (elements which are in one of the sets, but not in both). For instance, for the sets and , the symmetric difference set is . It is the set difference of the union and the intersection, .
Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

of and , denoted , is the set whose members are all possible ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...

s where is a member of and is a member of . The cartesian product of
Power set of a set is the set whose members are all possible subsets of . For example, the power set of is .

Some basic sets of central importance are the empty set

Empty set

In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...

(the unique set containing no elements), the set of natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

s, and the set of real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

Some ontology

A set is pure if all of its members are sets, all members of its members are sets, and so on. For example, the set containing only the empty set is a nonempty pure set. In modern set theory, it is common to restrict attention to the von Neumann universe
Von Neumann universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...

of pure sets, and many systems of axiomatic set theory are designed to axiomatize the pure sets only. There are many technical advantages to this restriction, and little generality is lost, since essentially all mathematical concepts can be modeled by pure sets. Sets in the von Neumann universe are organized into a cumulative hierarchy, based on how deeply their members, members of members, etc. are nested. Each set in this hierarchy is assigned (by transfinite recursion) an ordinal number

Ordinal number

In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...

α, known as its rank. The rank of a pure set X is defined to be one more than the least upper bound of the ranks of all members of X. For example, the empty set is assigned rank 0, while the set containing only the empty set is assigned rank 1. For each ordinal α, the set V_α is defined to consist of all pure sets with rank less than α. The entire von Neumann universe is denoted V.

Axiomatic set theory

Elementary set theory can be studied informally and intuitively, and so can be taught in primary schools using, say, Venn diagram

Venn diagram

Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...

s. The intuitive approach tacitly assumes that a set may be formed from the class of all objects satisfying any particular defining condition. This assumption gives rise to paradoxes, the simplest and best known of which are Russell's paradox

Russell's paradox

In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...

and the Burali-Forti paradox

Burali-Forti paradox

In set theory, a field of mathematics, the Burali-Forti paradox demonstrates that naively constructing "the set of all ordinal numbers" leads to a contradiction and therefore shows an antinomy in a system that allows its construction...

. Axiomatic set theory was originally devised to rid set theory of such paradoxes.

The most widely studied systems of axiomatic set theory imply that all sets form a cumulative hierarchy. Such systems come in two flavors, those whose ontology

Ontology

Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...

consists of:

Sets alone. This includes the most common axiomatic set theory, Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...

(ZFC), which includes the axiom of choice. Fragments of ZFC include:
- Zermelo set theory
  Zermelo set theory
  Zermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo, is the ancestor of modern set theory. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted...
  
  , which replaces the axiom schema of replacement
  Axiom schema of replacement
  In set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
  
  with that of separation;
- General set theory
  General set theory
  General set theory is George Boolos's name for a fragment of the axiomatic set theory Z. GST is sufficient for all mathematics not requiring infinite sets, and is the weakest known set theory whose theorems include the Peano axioms.-Ontology:...
  
  , a small fragment of Zermelo set theory
  Zermelo set theory
  Zermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo, is the ancestor of modern set theory. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted...
  
  sufficient for the Peano axioms
  Peano axioms
  In mathematical logic, the Peano axioms, also known as the Dedekind–Peano axioms or the Peano postulates, are a set of axioms for the natural numbers presented by the 19th century Italian mathematician Giuseppe Peano...
  
  and finite sets;
- Kripke-Platek set theory, which omits the axioms of infinity, powerset
  Axiom of power set
  In mathematics, the axiom of power set is one of the Zermelo–Fraenkel axioms of axiomatic set theory.In the formal language of the Zermelo–Fraenkel axioms, the axiom reads:...
  
  , and choice, and weakens the axiom schemata of separation and replacement
  Axiom schema of replacement
  In set theory, the axiom schema of replacement is a schema of axioms in Zermelo–Fraenkel set theory that asserts that the image of any set under any definable mapping is also a set...
  
  .
Sets and proper classes. This includes Von Neumann-Bernays-Gödel set theory, which has the same strength as ZFC for theorems about sets alone, and Morse-Kelley set theory, which is stronger than ZFC.

The above systems can be modified to allow urelements, objects that can be members of sets but that are not themselves sets and do not have any members.

The systems of New Foundations
New Foundations
In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...

NFU (allowing urelements) and NF (lacking them) are not based on a cumulative hierarchy. NF and NFU include a "set of everything," relative to which every set has a complement. In these systems urelements matter, because NF, but not NFU, produces sets for which the axiom of choice does not hold.

Systems of constructive set theory

Constructive set theory

Constructive set theory is an approach to mathematical constructivism following the program of axiomatic set theory. That is, it uses the usual first-order language of classical set theory, and although of course the logic is constructive, there is no explicit use of constructive types...

, such as CST, CZF, and IZF, embed their set axioms in intuitionistic logic

Intuitionistic logic

Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...

instead of first order logic. Yet other systems accept standard first order logic but feature a nonstandard membership relation. These include rough set theory

Rough set

In computer science, a rough set, first described by a Polish computer scientist Zdzisław I. Pawlak, is a formal approximation of a crisp set in terms of a pair of sets which give the lower and the upper approximation of the original set...

and fuzzy set theory, in which the value of an atomic formula

Atomic formula

In mathematical logic, an atomic formula is a formula with no deeper propositional structure, that is, a formula that contains no logical connectives or equivalently a formula that has no strict subformulas. Atoms are thus the simplest well-formed formulas of the logic...

embodying the membership relation is not simply True or False. The Boolean-valued model

Boolean-valued model

In mathematical logic, a Boolean-valued model is a generalization of the ordinary Tarskian notion of structure from model theory. In a Boolean-valued model, the truth values of propositions are not limited to "true" and "false", but instead take values in some fixed complete Boolean...

s of ZFC are a related subject.

An enrichment of ZFC called Internal Set Theory

Internal set theory

Internal set theory is a mathematical theory of sets developed by Edward Nelson that provides an axiomatic basis for a portion of the non-standard analysis introduced by Abraham Robinson. Instead of adding new elements to the real numbers, the axioms introduce a new term, "standard", which can be...

was proposed by Edward Nelson

Edward Nelson

Edward Nelson is a professor in the Mathematics Department at Princeton University. He is known for his work on mathematical physics and mathematical logic...

in 1977.

Applications

Many mathematical concepts can be defined precisely using only set theoretic concepts. For example, mathematical structures as diverse as graphs

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

, manifolds, rings

Ring (mathematics)

In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...

, and vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

s can all be defined as sets satisfying various (axiomatic) properties. Equivalence

Equivalence relation

In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...

and order relations are ubiquitous in mathematics, and the theory of mathematical relations

Relation (mathematics)

In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...

can be described in set theory.

Set theory is also a promising foundational system for much of mathematics. Since the publication of the first volume of Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...

, it has been claimed that most or even all mathematical theorems can be derived using an aptly designed set of axioms for set theory, augmented with many definitions, using first or second order logic. For example, properties of the natural

Natural number

and real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s can be derived within set theory, as each number system can be identified with a set of equivalence classes under a suitable equivalence relation

Equivalence relation

whose field is some infinite set.

Set theory as a foundation for mathematical analysis

Mathematical analysis

Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...

, topology

Topology

Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...

, abstract algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

, and discrete mathematics

Discrete mathematics

Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...

is likewise uncontroversial; mathematicians accept that (in principle) theorems in these areas can be derived from the relevant definitions and the axioms of set theory. Few full derivations of complex mathematical theorems from set theory have been formally verified, however, because such formal derivations are often much longer than the natural language proofs mathematicians commonly present. One verification project, Metamath

Metamath

Metamath is a computer-assisted proof checker. It has no specific logic embedded and can simply be regarded as a device to apply inference rules to formulas...

, includes derivations of more than 10,000 theorems starting from the ZFC axioms and using first order logic.

Areas of study

Set theory is a major area of research in mathematics, with many interrelated subfields.

Combinatorial set theory

Combinatorial set theory concerns extensions of finite combinatorics

Combinatorics

Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...

to infinite sets. This includes the study of cardinal arithmetic and the study of extensions of Ramsey's theorem

Ramsey's theorem

In combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...

such as the Erdős–Rado theorem

Erdős–Rado theorem

In partition calculus, part of combinatorial set theory, which is a branch of mathematics, the Erdős–Rado theorem is a basic result, extending Ramsey's theorem to uncountable sets.-Statement of the theorem:If r≥2 is finite, κ is an infinite cardinal, then...

Descriptive set theory

Descriptive set theory is the study of subsets of the real line

Real line

In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...

and, more generally, subsets of Polish space

Polish space

In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...

s. It begins with the study of pointclass

Pointclass

In the mathematical field of descriptive set theory, a pointclass is a collection of sets of points, where a point is ordinarily understood to be an element of some perfect Polish space. In practice, a pointclass is usually characterized by some sort of definability property; for example, the...

es in the Borel hierarchy

Borel hierarchy

In mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set...

and extends to the study of more complex hierarchies such as the projective hierarchy and the Wadge hierarchy

Wadge hierarchy

In descriptive set theory, Wadge degrees are levels of complexity for sets of reals. Sets are compared by continuous reductions. The Wadge hierarchy is the structure of Wadge degrees.- Wadge degrees :...

. Many properties of Borel sets can be established in ZFC, but proving these properties hold for more complicated sets requires additional axioms related to determinacy and large cardinals.

The field of effective descriptive set theory

Effective descriptive set theory

Effective descriptive set theory is the branch of descriptive set theory dealing with sets of reals having lightface definitions; that is, definitions that do not require an arbitrary real parameter. Thus effective descriptive set theory combines descriptive set theory with recursion theory....

is between set theory and recursion theory

Recursion theory

Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...

. It includes the study of lightface pointclasses, and is closely related to hyperarithmetical theory

Hyperarithmetical theory

In recursion theory, hyperarithmetic theory is a generalization of Turing computability. It has close connections with definability in second-order arithmetic and with weak systems of set theory such as Kripke–Platek set theory...

. In many cases, results of classical descriptive set theory have effective versions; in some cases, new results are obtained by proving the effective version first and then extending ("relativizing") it to make it more broadly applicable.

A recent area of research concerns Borel equivalence relation

Borel equivalence relation

In mathematics, a Borel equivalence relation on a Polish space X is an equivalence relation on X that is a Borel subset of X × X....

s and more complicated definable equivalence relation

Equivalence relation

s. This has important applications to the study of invariants

Invariant (mathematics)

In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...

in many fields of mathematics.

Fuzzy set theory

In set theory as Cantor

Georg Cantor

defined and Zermelo and Fraenkel axiomatized, an object is either a member of a set or not. In fuzzy set theory this condition was relaxed by Lotfi A. Zadeh so an object has a degree of membership in a set, as number between 0 and 1. For example, the degree of membership of a person in the set of "tall people" is more flexible than a simple yes or no answer and can be a real number such as 0.75.

Inner model theory

An inner model of Zermelo–Fraenkel set theory (ZF) is a transitive class that includes all the ordinals and satisfies all the axioms of ZF. The canonical example is the constructible universe

Constructible universe

In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...

L developed by Gödel.
One reason that the study of inner models is of interest is that it can be used to prove consistency results. For example, it can be shown that regardless whether a model V of ZF satisfies the continuum hypothesis

Continuum hypothesis

In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...

or the axiom of choice, the inner model L constructed inside the original model will satisfy both the generalized continuum hypothesis and the axiom of choice. Thus the assumption that ZF is consistent (has any model whatsoever) implies that ZF together with these two principles is consistent.

The study of inner models is common in the study of determinacy

Axiom of determinacy

The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...

and large cardinals, especially when considering axioms such as the axiom of determinacy that contradict the axiom of choice. Even if a fixed model of set theory satisfies the axiom of choice, it is possible for an inner model to fail to satisfy the axiom of choice. For example, the existence of sufficiently large cardinals implies that there is an inner model satisfying the axiom of determinacy (and thus not satisfying the axiom of choice).

Large cardinals

A large cardinal is a cardinal number with an extra property. Many such properties are studied, including inaccessible cardinal

Inaccessible cardinal

In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...

s, measurable cardinal

Measurable cardinal

- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...

s, and many more. These properties typically imply the cardinal number must be very large, with the existence of a cardinal with the specified property unprovable in Zermelo-Fraenkel set theory.

Determinacy

Determinacy refers to the fact that, under appropriate assumptions, certain two-player games of perfect information are determined from the start in the sense that one player must have a winning strategy. The existence of these strategies has important consequences in descriptive set theory, as the assumption that a broader class of games is determined often implies that a broader class of sets will have a topological property. The axiom of determinacy

Axiom of determinacy

The axiom of determinacy is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person games of length ω with perfect information...

(AD) is an important object of study; although incompatible with the axiom of choice, AD implies that all subsets of the real line are well behaved (in particular, measurable and with the perfect set property). AD can be used to prove that the Wadge degrees have an elegant structure.

Forcing

Paul Cohen

Paul Cohen (mathematician)

Paul Joseph Cohen was an American mathematician best known for his proof of the independence of the continuum hypothesis and the axiom of choice from Zermelo–Fraenkel set theory, the most widely accepted axiomatization of set theory.-Early years:Cohen was born in Long Branch, New Jersey, into a...

invented the method of forcing

Forcing (mathematics)

In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...

while searching for a model

Model theory

In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....

of ZFC in which the axiom of choice or the continuum hypothesis

Continuum hypothesis

fails. Forcing adjoins to some given model of set theory additional sets in order to create a larger model with properties determined (i.e. "forced") by the construction and the original model. For example, Cohen's construction adjoins additional subsets of the natural number

Natural number

s without changing any of the cardinal number

Cardinal number

s of the original model. Forcing is also one of two methods for proving relative consistency by finitistic methods, the other method being Boolean-valued model

Boolean-valued model

Cardinal invariants

A cardinal invariant is a property of the real line measured by a cardinal number. For example, a well-studied invariant is the smallest cardinality of a collection of meagre set

Meagre set

In the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...

s of reals whose union is the entire real line. These are invariants in the sense that any two isomorphic models of set theory must give the same cardinal for each invariant. Many cardinal invariants have been studied, and the relationships between them are often complex and related to axioms of set theory.

Set-theoretic topology

Set-theoretic topology studies questions of general topology

General topology

In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...

that are set-theoretic in nature or that require advanced methods of set theory for their solution. Many of these theorems are independent of ZFC, requiring stronger axioms for their proof. A famous problem is the normal Moore space question

Moore space (topology)

In mathematics, more specifically point-set topology, a Moore space is a developable regular Hausdorff space. Equivalently, a topological space X is a Moore space if the following conditions hold:...

, a question in general topology that was the subject of intense research. The answer to the normal Moore space question was eventually proved to be independent of ZFC.

Objections to set theory as a foundation for mathematics

From set theory's inception, some mathematicians objected to it

Controversy over Cantor's theory

In mathematical logic, the theory of infinite sets was first developed by Georg Cantor. Although this work has found wide acceptance in the mathematics community, it has been criticized in several areas by mathematicians and philosophers....

as a foundation for mathematics

Foundations of mathematics

Foundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...

, arguing, for example, that it is just a game which includes elements of fantasy. The most common objection to set theory, one Kronecker voiced in set theory's earliest years, starts from the constructivist view that mathematics is loosely related to computation. If this view is granted, then the treatment of infinite sets, both in naive

Naive set theory

and in axiomatic set theory, introduces into mathematics methods and objects that are not computable even in principle. Ludwig Wittgenstein

Ludwig Wittgenstein

Ludwig Josef Johann Wittgenstein was an Austrian philosopher who worked primarily in logic, the philosophy of mathematics, the philosophy of mind, and the philosophy of language. He was professor in philosophy at the University of Cambridge from 1939 until 1947...

questioned the way Zermelo–Fraenkel set theory

Zermelo–Fraenkel set theory

handled infinities. Wittgenstein's views about the foundations of mathematics were later criticised by Georg Kreisel

Georg Kreisel

Georg Kreisel FRS is an Austrian-born mathematical logician who has studied and worked in Great Britain and America. Kreisel came from a Jewish background; his family sent him to England before the Anschluss, where he studied mathematics at Trinity College, Cambridge and then, during World War...

and Paul Bernays

Paul Bernays

Paul Isaac Bernays was a Swiss mathematician, who made significant contributions to mathematical logic, axiomatic set theory, and the philosophy of mathematics. He was an assistant to, and close collaborator of, David Hilbert.-Biography:Bernays spent his childhood in Berlin. Bernays attended the...

, and closely investigated by Crispin Wright

Crispin Wright

Crispin Wright is a British philosopher, who has written on neo-Fregean philosophy of mathematics, Wittgenstein's later philosophy, and on issues related to truth, realism, cognitivism, skepticism, knowledge, and objectivity....

, among others.

Category theorists

Category theory

Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...

have proposed topos theory as an alternative to traditional axiomatic set theory. Topos theory can interpret various alternatives to that theory, such as constructivism, finite set theory, and computable

Turing machine

A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...

set theory.

External links

Foreman, M.
Matthew Foreman
Matthew Dean Foreman is a set theorist at University of California, Irvine. He has made contributions in widely varying areas of set theory, including descriptive set theory, forcing, and infinitary combinatorics....

, Akihiro Kanamori
Akihiro Kanamori
is a Japan-born American mathematician. He specializes in set theory and is the author of the successful monograph on large cardinals, The Higher Infinite. He wrote several essays on the history of mathematics, especially set theory.Kanamori graduated from California Institute of Technology and...

, eds. Handbook of Set Theory. 3 vols., 2010. Each chapter surveys some aspect of contemporary research in set theory. Does not cover established elementary set theory, on which see Devlin (1993).
Arthur Schoenflies (1898) Mengenlehre in Klein's encyclopedia
Klein's encyclopedia
In mathematics, Klein’s encyclopedia refers to a German mathematical encyclopedia published in six volumes from 1898 to 1933. Felix Klein and Wilhelm Meyer were organizers of the encyclopedia. Its title in English is "Encyclopedia of mathematical sciences including their applications", which is...

.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

History

Basic concepts

Some ontology

Axiomatic set theory

Applications

Areas of study

Combinatorial set theory

Descriptive set theory

Fuzzy set theory

Inner model theory

Large cardinals

Determinacy

Forcing

Cardinal invariants

Set-theoretic topology

Objections to set theory as a foundation for mathematics

See also

Further reading

External links