Graph (mathematics) - AbsoluteAstronomy.com

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges. Typically, a graph is depicted in diagrammatic form as a set of dots for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics

Discrete mathematics

Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...

.

The edges may be directed (asymmetric) or undirected (symmetric). For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this is an undirected graph, because if person A shook hands with person B, then person B also shook hands with person A. On the other hand, if the vertices represent people at a party, and there is an edge from person A to person B when person A knows of person B, then this graph is directed, because knowing of someone is not necessarily a symmetric relation

Symmetric relation

In mathematics, a binary relation R over a set X is symmetric if it holds for all a and b in X that if a is related to b then b is related to a.In mathematical notation, this is:...

(that is, one person knowing of another person does not necessarily imply the reverse; for example, many fans may know of a celebrity

Celebrity

A celebrity, also referred to as a celeb in popular culture, is a person who has a prominent profile and commands a great degree of public fascination and influence in day-to-day media...

, but the celebrity is unlikely to know of all their fans). This latter type of graph is called a directed graph and the edges are called directed edges or arcs.

Vertices are also called nodes or points, and edges are also called lines. Graphs are the basic subject studied by graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

. The word "graph" was first used in this sense by J.J. Sylvester

James Joseph Sylvester

James Joseph Sylvester was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory and combinatorics...

in 1878.

Definitions

Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures.

Graph

In the most common sense of the term, a graph is an ordered pair

Ordered pair

In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...

G = (V, E) comprising a set V of vertices or nodes together with a set E of edges or lines, which are 2-element subsets of V (i.e., an edge is related with two vertices, and the relation is represented as unordered pair of the vertices with respect to the particular edge). To avoid ambiguity, this type of graph may be described precisely as undirected and simple.

Other senses of graph stem from different conceptions of the edge set. In one more generalized notion, E is a set together with a relation of incidence that associates with each edge two vertices. In another generalized notion, E is a multiset
Multiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...

of unordered pairs of (not necessarily distinct) vertices. Many authors call this type of object a multigraph
Multigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....

or pseudograph.

All of these variants and others are described more fully below.

The vertices belonging to an edge are called the ends, endpoints, or end vertices of the edge. A vertex may exist in a graph and not belong to an edge.

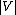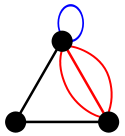
V and E are usually taken to be finite, and many of the well-known results are not true (or are rather different) for infinite graphs because many of the arguments fail in the infinite case. The order of a graph is (the number of vertices). A graph's size is 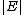, the number of edges. The degree of a vertex is the number of edges that connect to it, where an edge that connects to the vertex at both ends (a loop

Loop (graph theory)

In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....

) is counted twice.

For an edge {u, v}, graph theorists usually use the somewhat shorter notation uv.

Adjacency relation

The edges E of an undirected graph G induce a symmetric binary relation ~ on V that is called the adjacency relation of G. Specifically, for each edge {u, v} the vertices u and v are said to be adjacent to one another, which is denoted u ~ v.

Distinction in terms of the main definition

As stated above, in different contexts it may be useful to define the term graph with different degrees of generality. Whenever it is necessary to draw a strict distinction, the following terms are used. Most commonly, in modern texts in graph theory, unless stated otherwise, graph means "undirected simple finite graph" (see the definitions below).

Undirected graph

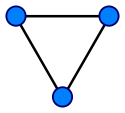
An undirected graph is one in which edges have no orientation. The edge (a, b) is identical to the edge (b, a), i.e., they are not ordered pairs, but sets {u, v} (or 2-multisets) of vertices.

Directed graph

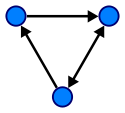
A directed graph or digraph is an ordered pair D = (V, A) with

V a set whose elements are called vertices or nodes, and

A a set of ordered pairs of vertices, called arcs, directed edges, or arrows.

An arc a = (x, y) is considered to be directed from x to y; y is called the head and x is called the tail of the arc; y is said to be a direct successor of x, and x is said to be a direct predecessor of y. If a path
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...

leads from x to y, then y is said to be a successor of x and reachable from x, and x is said to be a predecessor of y. The arc (y, x) is called the arc (x, y) inverted.

A directed graph D is called symmetric if, for every arc in D, the corresponding inverted arc also belongs to D. A symmetric loopless directed graph D = (V, A) is equivalent to a simple undirected graph G = (V, E), where the pairs of inverse arcs in A correspond 1-to-1 with the edges in E; thus the edges in G number |E| = |A|/2, or half the number of arcs in D.

A variation on this definition is the oriented graph, in which not more than one of (x, y) and (y, x) may be arcs.

Mixed graph
A mixed graph G is a graph in which some edges may be directed and some may be undirected.
It is written as an ordered triple G = (V, E, A) with V, E, and A defined as above.
Directed and undirected graphs are special cases.

Multigraph

A loop

Loop (graph theory)

In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....

is an edge (directed or undirected) which starts and ends on the same vertex; these may be permitted or not permitted according to the application. In this context, an edge with two different ends is called a link.

The term "multigraph

Multigraph

In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....

" is generally understood to mean that multiple edges

Multiple edges

In graph theory, multiple edges , are two or more edges that are incident to the same two vertices...

(and sometimes loops) are allowed. Where graphs are defined so as to allow loops and multiple edges, a multigraph is often defined to mean a graph without loops, however, where graphs are defined so as to disallow loops and multiple edges, the term is often defined to mean a "graph" which can have both multiple edges and loops, although many use the term "pseudograph" for this meaning.

Simple graph

As opposed to a multigraph, a simple graph is an undirected graph that has no loops

Loop (graph theory)

In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....

and no more than one edge between any two different vertices. In a simple graph the edges of the graph form a set (rather than a multiset

Multiset

In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...

) and each edge is a distinct pair of vertices. In a simple graph with n vertices every vertex has a degree that is less than n (the converse, however, is not true - there exist non-simple graphs with n vertices in which every vertex has a degree smaller than n).

Weighted graph

A graph is a weighted graph if a number (weight) is assigned to each edge. Such weights might represent, for example, costs, lengths or capacities, etc. depending on the problem at hand.

Half-edges, loose edges

In exceptional situations it is even necessary to have edges with only one end, called half-edges, or no ends (loose edges); see for example signed graphs and biased graph

Biased graph

In mathematics, a biased graph is a graph with a list of distinguished circles , such that if two circles in the list are contained in a theta graph, then so is the third circle of the theta graph...

Regular graph

A regular graph is a graph where each vertex has the same number of neighbors, i.e., every vertex has the same degree or valency. A regular graph with vertices of degree k is called a k‑regular graph or regular graph of degree k.

Complete graph

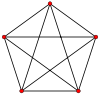
Complete graphs have the feature that each pair of vertices has an edge connecting them.

Finite and infinite graphs

A finite graph is a graph G = (V, E) such that V and E are finite sets. An infinite graph is one with an infinite set of vertices or edges or both.

Most commonly in graph theory it is implied that the graphs discussed are finite. If the graphs are infinite, that is usually specifically stated.

Graph classes in terms of connectivity

In an undirected graph G, two vertices

Vertex (graph theory)

In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

u and v are called connected if G contains a path
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...

from u to v. Otherwise, they are called disconnected. A graph is called connected if every pair of distinct vertices in the graph is connected; otherwise, it is called disconnected.

A graph is called k-vertex-connected

K-vertex-connected graph

In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...

or k-edge-connected
K-edge-connected graph
In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G = be an arbitrary graph....

if no set of k-1 vertices (respectively, edges) exists that, when removed, disconnects the graph. A k-vertex-connected graph is often called simply k-connected.

A directed graph

Directed graph

A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...

is called weakly connected if replacing all of its directed edges with undirected edges produces a connected (undirected) graph. It is strongly connected or strong if it contains a directed path from u to v and a directed path from v to u for every pair of vertices u, v.

Properties of graphs

Two edges of a graph are called adjacent (sometimes coincident) if they share a common vertex. Two arrows of a directed graph are called consecutive if the head of the first one is at the nock (notch end) of the second one. Similarly, two vertices are called adjacent if they share a common edge (consecutive if they are at the notch and at the head of an arrow), in which case the common edge is said to join the two vertices. An edge and a vertex on that edge are called incident.

The graph with only one vertex and no edges is called the trivial graph. A graph with only vertices and no edges is known as an edgeless graph. The graph with no vertices and no edges is sometimes called the null graph or empty graph, but the terminology is not consistent and not all mathematicians allow this object.

In a weighted graph or digraph, each edge is associated with some value, variously called its cost, weight, length or other term depending on the application; such graphs arise in many contexts, for example in optimal routing problems such as the traveling salesman problem.

Normally, the vertices of a graph, by their nature as elements of a set, are distinguishable. This kind of graph may be called vertex-labeled. However, for many questions it is better to treat vertices as indistinguishable; then the graph may be called unlabeled. (Of course, the vertices may be still distinguishable by the properties of the graph itself, e.g., by the numbers of incident edges). The same remarks apply to edges, so graphs with labeled edges are called edge-labeled graphs. Graphs with labels attached to edges or vertices are more generally designated as labeled. Consequently, graphs in which vertices are indistinguishable and edges are indistinguishable are called unlabeled. (Note that in the literature the term labeled may apply to other kinds of labeling, besides that which serves only to distinguish different vertices or edges.)

Examples

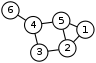
The diagram at right is a graphic representation of the following graph:

V = {1, 2, 3, 4, 5, 6}

E = .

In category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...

a small category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...

can be represented by a directed multigraph
Multigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....

in which the objects of the category represented as vertices and the morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...

s as directed edges. Then, the functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....

s between categories induce some, but not necessarily all, of the digraph morphisms of the graph.
In computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...

, directed graphs are used to represent knowledge (e.g., Conceptual graph
Conceptual graph
Conceptual graphs are a formalism for knowledge representation. In the first published paper on CGs, John F. Sowa used them to represent the conceptual schemas used in database systems...

), finite state machine
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...

s, and many other discrete structures.
A binary relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...

R on a set X defines a directed graph. An element x of X is a direct predecessor of an element y of X iff xRy.

Important graphs

Basic examples are:

In a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

, each pair of vertices is joined by an edge; that is, the graph contains all possible edges.
In a bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...

, the vertex set can be partitioned
Partition of a set
In mathematics, a partition of a set X is a division of X into non-overlapping and non-empty "parts" or "blocks" or "cells" that cover all of X...

into two sets, W and X, so that no two vertices in W are adjacent and no two vertices in X are adjacent. Alternatively, it is a graph with a chromatic number of 2.
In a complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...

, the vertex set is the union of two disjoint sets, W and X, so that every vertex in W is adjacent to every vertex in X but there are no edges within W or X.
In a linear graph or path graph
Path graph
In the mathematical field of graph theory, a path graph or linear graph is a particularly simple example of a tree, namely a tree with two or more vertices that is not branched at all, that is, contains only vertices of degree 2 and 1...

of length n, the vertices can be listed in order, v₀, v₁, ..., v_n, so that the edges are v_i−1v_i for each i = 1, 2, ..., n. If a linear graph occurs as a subgraph of another graph, it is a path
Path (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...

in that graph.
In a cycle graph
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...

of length n ≥ 3, vertices can be named v₁, ..., v_n so that the edges are v_i−1v_i for each i = 2,...,n in addition to v_nv₁. Cycle graphs can be characterized as connected
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...

2-regular
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...

graphs. If a cycle graph occurs as a subgraph of another graph, it is a cycle or circuit in that graph.
A planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...

is a graph whose vertices and edges can be drawn in a plane such that no two of the edges intersect (i.e., embedded in a plane).
A tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...

is a connected graph with no cycles.
A forest is a graph with no cycles (i.e. the disjoint union of one or more trees).

More advanced kinds of graphs are:

The Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...

and its generalizations
Perfect graph
Perfect graph
In graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....

s
Cograph
Cograph
In graph theory, a cograph, or complement-reducible graph, or P4-free graph, is a graph that can be generated from the single-vertex graph K1 by complementation and disjoint union...

s
Chordal graph
Chordal graph
In the mathematical area of graph theory, a graph is chordal if each of its cycles of four or more nodes has a chord, which is an edge joining two nodes that are not adjacent in the cycle. An equivalent definition is that any chordless cycles have at most three nodes...

s
Other graphs with large automorphism groups
Graph automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....

: vertex-transitive
Vertex-transitive graph
In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...

, arc-transitive, and distance-transitive graph
Distance-transitive graph
In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y.A distance transitive...

s.
Strongly regular graph
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...

s and their generalization distance-regular graph
Distance-regular graph
In mathematics, a distance-regular graph is a regular graph such that for any two vertices v and w at distance i the number of vertices adjacent to w and at distance j from v is the same. Every distance-transitive graph is distance-regular...

s.

Operations on graphs

There are several operations that produce new graphs from old ones, which might be classified into the following categories:

Elementary operations, sometimes called "editing operations" on graphs, which create a new graph from the original one by a simple, local change, such as addition or deletion of a vertex or an edge, merging and splitting of vertices, etc.
Graph rewrite operations
Graph rewriting
Graph transformation, or Graph rewriting, concerns the technique of creating a new graph out of an original graph using some automatic machine. It has numerous applications, ranging from software verification to layout algorithms....

replacing the occurrence of some pattern graph within the host graph by an instance of the corresponding replacement graph.
Unary operations, which create a significantly new graph from the old one. Examples:
- Line graph
  Line graph
  In graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...
- Dual graph
  Dual graph
  In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
- Complement graph
  Complement graph
  In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
Binary operations, which create new graph from two initial graphs. Examples:
- Disjoint union of graphs
- Cartesian product of graphs
  Cartesian product of graphs
  In graph theory, the Cartesian product G \square H of graphs G and H is a graph such that* the vertex set of G \square H is the Cartesian product V × V; and...
- Tensor product of graphs
  Tensor product of graphs
  In graph theory, the tensor product G × H of graphs G and H is a graph such that* the vertex set of G × H is the Cartesian product V × V; and...
- Strong product of graphs
  Strong product of graphs
  In graph theory, the strong product G ⊠ H of graphs G and H is a graph such that* the vertex set of G ⊠ H is the Cartesian product V × V; and...
- Lexicographic product of graphs
  Lexicographic product of graphs
  In graph theory, the lexicographic product or graph composition of graphs and is a graph such that* the vertex set of is the cartesian product ; and...

Generalizations

In a hypergraph

Hypergraph

In mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...

, an edge can join more than two vertices.

An undirected graph can be seen as a simplicial complex

Simplicial complex

In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...

consisting of 1-simplices

Simplex

In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...

(the edges) and 0-simplices (the vertices). As such, complexes are generalizations of graphs since they allow for higher-dimensional simplices.

Every graph gives rise to a matroid

Matroid

In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....

.

In model theory

Model theory

In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....

, a graph is just a structure. But in that case, there is no limitation on the number of edges: it can be any cardinal number

Cardinal number

In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...

, see continuous graph.

In computational biology

Computational biology

Computational biology involves the development and application of data-analytical and theoretical methods, mathematical modeling and computational simulation techniques to the study of biological, behavioral, and social systems...

, power graph analysis

Power graph analysis

In computational biology, power graph analysis is a method for the analysis andrepresentation of complex networks. Power graph analysis is the computation, analysis and visual representation of a power graph from a graphs ....

introduces power graphs as an alternative representation of undirected graphs.

In geographic information systems, geometric networks

Geometric networks

A geometric network is an object commonly used in geographic information systems to model a series of interconnected features. A geometric network is similar to a graph in mathematics and computer science, and can be described and analyzed using theories and concepts similar to graph theory...

are closely modeled after graphs, and borrow many concepts from graph theory

Graph theory

to perform spatial analysis on road networks or utility grids.

External links

A searchable database of small connected graphs
VisualComplexity.com — A visual exploration on mapping complex networks
Intelligent Graph Visualizer — IGV create and edit graph, automatically places graph, search shortest path (+coloring vertices), center, degree, eccentricity, etc.
Visual Graph Editor 2 — VGE2 designed for quick and easy creation, editing and saving of graphs and analysis of problems connected with graphs.
GraphsJ 2 — GraphsJ is a didactic Java software which features an easy-to-use GUI and interactively solves step-by-step many graph problems executing their associated algorithms.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Definitions

Graph

Adjacency relation

Distinction in terms of the main definition

Undirected graph

Directed graph

Mixed graph

Multigraph

Simple graph

Weighted graph

Half-edges, loose edges

Regular graph

Complete graph

Finite and infinite graphs

Graph classes in terms of connectivity

Properties of graphs

Examples

Important graphs

Operations on graphs

Generalizations

See also

External links