In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = (V,E) be a regular graph

Regular graph

In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...

 with v vertices and degree k. G is said to be strongly regular if there are also integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s λ and μ such that:

• Every two adjacent vertices have λ common neighbours.

• Every two non-adjacent vertices have μ common neighbours.

A graph of this kind is sometimes said to be an srg(v,k,λ,μ).

Some authors exclude graphs which satisfy the definition trivially, namely those graphs which are the disjoint union of one or more equal-sized complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

s, and their complements

Complement graph

In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...

, the Turán graph

Turán graph

The Turán graph T is a graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge whenever they belong to different subsets. The graph will have subsets of size \lceil n/r\rceil, and r- subsets of size \lfloor n/r\rfloor...

s.

A strongly regular graph is a distance-regular graph

Distance-regular graph

In mathematics, a distance-regular graph is a regular graph such that for any two vertices v and w at distance i the number of vertices adjacent to w and at distance j from v is the same. Every distance-transitive graph is distance-regular...

 with diameter 2, but only if μ is non-zero.

Properties

• The four parameters in an srg(v,k,λ,μ) are not independent, as it is easy to show that:

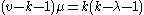
• Let I denote the identity matrix (of order v) and let J denote the matrix whose entries all equal 1. The adjacency matrix
  Adjacency matrix
  In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
  
   A of a strongly regular graph satisfies these properties :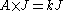
  • 
    (This is a trivial restatement of the vertex degree requirement).
  • 
    (The first term gives the number of 2-step paths from each vertex to all vertices. For the vertex pairs directly connected by an edge, the equation reduces to the number of such 2-step paths being equal to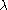 . For the vertex pairs not directly connected by an edge, the equation reduces to the number of such 2-step paths being equal to 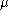. For the trivial self-pairs, the equation reduces to the degree being equal to k).

• The graph has exactly three eigenvalues:
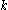  • whose multiplicity is 1
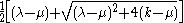  • whose multiplicity is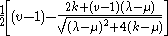
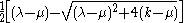  • whose multiplicity is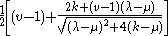

• Strongly regular graphs for which 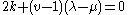are called conference graph
  Conference graph
  In the mathematical area of graph theory, a conference graph is a strongly regular graph with parameters v, and It is the graph associated with a symmetric conference matrix, and consequently its order v must be 1 and a sum of two squares....
  
  s because of their connection with symmetric conference matrices
  Conference matrix
  In mathematics, a conference matrix is a square matrix C with 0 on the diagonal and +1 and −1 off the diagonal, such that CTC is a multiple of the identity matrix I...
  
  . Their parameters reduce to .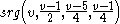

• Strongly regular graphs for which 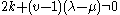have integer eigenvalues with unequal multiplicities.

• The complement
  Complement graph
  In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
  
   of an srg(v,k,λ,μ) is also strongly regular. It is an srg(v, v−k−1, v−2−2k+μ, v−2k+λ).

Examples

• The Shrikhande graph
  Shrikhande graph
  In the mathematical field of graph theory, the Shrikhande graph is a named graph discovered by S. S. Shrikhande in 1959. It is a strongly regular graph with 16 vertices and 48 edges, with each vertex having a degree of 6.-Properties:...
  
   is an srg(16,6,2,2) which is not a distance-transitive graph
  Distance-transitive graph
  In the mathematical field of graph theory, a distance-transitive graph is a graph such that, given any two vertices v and w at any distance i, and any other two vertices x and y at the same distance, there is an automorphism of the graph that carries v to x and w to y.A distance transitive...
  
  .
• The cycle
  Cycle graph
  In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
  
   of length 5 is an srg(5,2,0,1).
• The Petersen graph
  Petersen graph
  In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
  
   is an srg(10,3,0,1).
• The Chang graphs
  Chang graphs
  In the mathematical field of graph theory, the Chang graphs are a set of three 18-regular undirected graphs, each with 28 vertices and 168 edges.-External links:* * *...
  
   are srg(28,12,6,4).
• The Hoffman–Singleton graph is an srg(50,7,0,1).
• The M22 graph is an srg(77,16,0,4).
• The Higman–Sims graph is an srg(100,22,0,6).
• The Paley graph
  Paley graph
  In mathematics, and specifically graph theory, Paley graphs, named after Raymond Paley, are dense undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ in a quadratic residue. The Paley graphs form an infinite family of conference...
  
   of order q is an srg(q, (q − 1)/2, (q − 5)/4, (q − 1)/4).
• The n × n square rook's graph
  Rook's graph
  In graph theory, a rook's graph is a graph that represents all legal moves of the rook chess piece on a chessboard: each vertex represents a square on a chessboard and each edge represents a legal move...
  
   is an srg(n², 2n − 2, n − 2, 2).
• The Brouwer–Haemers graph
  Brouwer–Haemers graph
  In the mathematical field of graph theory, the Brouwer–Haemers graph is a 20-regular undirected graph with 81 vertices and 810 edges. It is the unique strongly regular graph with parameters .-External links:* *...
  
   is an srg(81,20,1,6).
• The Schläfli graph
  Schläfli graph
  In the mathematical field of graph theory, the Schläfli graph, named after Ludwig Schläfli, is a 16-regular undirected graph with 27 vertices and 216 edges. It is a strongly regular graph with parameters srg.-Construction:...
  
   is an srg(27,16,10,8).
• The Local McLaughlin graph
  Local McLaughlin graph
  In the mathematical field of graph theory, the local McLaughlin graph is a regular undirected graph with 162 vertices and 4536 edges. It is a strongly regular graph with parameters ....
  
   is an srg(162,56,10,24).

External links

• Eric W. Weisstein
  Eric W. Weisstein
  Eric W. Weisstein is an encyclopedist who created and maintains MathWorld and Eric Weisstein's World of Science . He currently works for Wolfram Research, Inc.-Education:...
  
  , Mathworld article with numerous examples.
• Gordon Royle
  Gordon Royle
  Gordon F. Royle is a Professor at the School of Mathematics and Statistics at The University of Western Australia. He is well known for his research into the mathematics of Sudoku and his search for the Sudoku puzzle with the smallest number of entries that has a unique solution.-See...
  
  , List of larger graphs and families.
• Andries E. Brouwer, Parameters of Strongly Regular Graphs.
• Brendan McKay
  Brendan McKay
  Brendan Damien McKay is a Professor in the Research School of Computer Science at the Australian National University . He has published extensively in combinatorics....
  
  , Some collections of graphs.
• Ted Spence, Strongly regular graphs on at most 64 vertices.