Petersen graph
Encyclopedia
In the mathematical
field of graph theory
, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen
, who in 1898 constructed it to be the smallest bridgeless
cubic graph
with no three-edge-coloring. Although the graph is generally credited to Petersen, it had in fact first appeared 12 years earlier, in a paper by .
Donald Knuth
states that the Petersen graph is "a remarkable configuration that serves as a counterexample to many optimistic predictions about what might be true for graphs in general."
of the line graph
of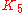
. It is also the Kneser graph
; this means that it has one vertex for each 2-element subset of a 5-element set, and two vertices are connected by an edge if and only if the corresponding 2-element subsets are disjoint from each other. As a Kneser graph of the form 
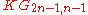it is an example of an odd graph
.
Geometrically, the Petersen graph is the graph formed by the vertices and edges of the hemi-dodecahedron
, that is, a dodecahedron with opposite points, lines and faces identified together.
. Any nonplanar graph has as minor
s either the complete graph
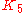, or the complete bipartite graph
, but the Petersen graph has both as minors. The 
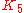minor can be formed by contracting the edges of a perfect matching, for instance the five short edges in the first picture. The 
minor can be formed by deleting one vertex (for instance the central vertex of the 3-symmetric drawing) and contracting an edge incident to each neighbor of the deleted vertex.
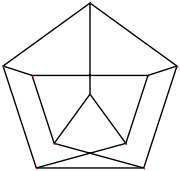The most common and symmetric plane drawing of the Petersen graph, as a pentagram within a pentagon, has five crossings. However, this is not the best drawing for minimizing crossings; there exists another drawing (shown in the figure) with only two crossings. Thus, the Petersen graph has crossing number 2. On a torus
the Petersen graph can be drawn without edge crossings; it therefore has orientable genus
1.
The Petersen graph can also be drawn (with crossings) in the plane in such a way that all the edges have equal length. That is, it is a unit distance graph
.
The simplest non-orientable surface
on which the Petersen graph can be embedded without crossings is the projective plane
. This is the embedding given by the hemi-dodecahedron
construction of the Petersen graph. The projective plane embedding can also be formed from the standard pentagonal drawing of the Petersen graph by placing a cross-cap
within the five-point star at the center of the drawing, and routing the star edges through this cross-cap; the resulting drawing has six pentagonal faces. This construction forms a regular map
and shows that the Petersen graph has non-orientable genus
1.
(with signature srg(10,3,0,1)). It is also symmetric
, meaning that it is edge transitive
and vertex transitive
. More strongly, it is 3-arc-transitive: every directed three-edge path in the Petersen graph can be transformed into every other such path by a symmetry of the graph.
It is one of only 13 cubic distance-regular graph
s.
The automorphism group
of the Petersen graph is the symmetric group
; the action of 
on the Petersen graph follows from its construction as a Kneser graph
. Every homomorphism
of the Petersen graph to itself that doesn't identify adjacent vertices is an automorphism. As shown in the figures, the drawings of the Petersen graph may exhibit five-way or three-way symmetry, but it is not possible to draw the Petersen graph in the plane in such a way that the drawing exhibits the full symmetry group of the graph.
Despite its high degree of symmetry, the Petersen graph is not a Cayley graph
. It is the smallest vertex-transitive graph that is not a Cayley graph.
but no Hamiltonian cycle. It is the smallest bridgeless cubic graph with no Hamiltonian cycle. It is hypohamiltonian
, meaning that although it has no Hamiltonian cycle, deleting any vertex makes it Hamiltonian, and is the smallest hypohamiltonian graph.
As a finite connected vertex-transitive graph that does not have a Hamiltonian cycle, the Petersen graph is a counterexample to a variant of the Lovász conjecture
, but the canonical formulation of the conjecture asks for a Hamiltonian path and is verified by the Petersen graph.
Only five vertex-transitive graphs with no Hamiltonian cycles are known: the complete graph
K2, the Petersen graph, the Coxeter graph
and two graphs derived from the Petersen and Coxeter graphs by replacing each vertex with a triangle. If G is a 2-connected, r-regular graph with at most 3r + 1 vertices, then G is Hamiltonian or G is the Petersen graph.
To see that the Petersen graph has no Hamiltonian cycle C, we describe the ten-vertex 3-regular graphs
that do have a Hamiltonian cycle and show that none of them is the Petersen graph, by finding a cycle in each of them that is shorter than any cycle in the Petersen graph. Any ten-vertex Hamiltonian 3-regular graph consists of a ten-vertex cycle C plus five chords. If any chord connects two vertices at distance two or three along C from each other, the graph has a 3-cycle or 4-cycle, and therefore cannot be the Petersen graph. If two chords connect opposite vertices of C to vertices at distance four along C, there is again a 4-cycle. The only remaining case is a Möbius ladder
formed by connecting each pair of opposite vertices by a chord, which again has a 4-cycle. Since the Petersen graph has girth five, it cannot be formed in this way and has no Hamiltonian cycle.
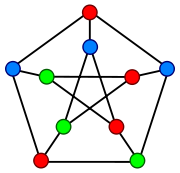The Petersen graph has chromatic number 3, meaning that its vertices can be colored
with three colors — but not with two — such that no edge connects vertices of the same color.
The Petersen graph has chromatic index 4; coloring the edges requires four colors. A proof of this requires checking four cases to demonstrate that no 3-edge-coloring exists. As a connected bridgeless cubic graph with chromatic index four, the Petersen graph is a snark
. It is the smallest possible snark, and was the only known snark from 1898 until 1946. The snark theorem
, a result conjectured by W. T. Tutte
and announced in 2001 by Robertson, Sanders, Seymour, and Thomas, states that every snark has the Petersen graph as a minor
.
Additionally, the graph has fractional chromatic index 3, proving that the difference between the chromatic index and fractional chromatic index can be as large as 1. The long-standing Goldberg-Seymour Conjecture proposes that this is the largest gap possible.
The Thue number
(a variant of the chromatic index) of the Petersen graph is 5.
G(n,k) is formed by connecting the vertices of a regular n-gon
to the corresponding vertices of a star polygon with Schläfli symbol {n/k}. For instance, in this notation, the Petersen graph is G(5,2): it can be formed by connecting corresponding vertices of a pentagon and five-point star, and the edges in the star connect every second vertex.
The generalized Petersen graphs also include the n-prism G(n,1)
the Dürer graph
G(6,2), the Möbius-Kantor graph
G(8,3), the dodecahedron G(10,2), the Desargues graph
G(10,3) and the Nauru graph
G(12,5).
The Petersen family
consists of the seven graphs that can be formed from the Petersen graph by zero or more applications of Δ-Y or Y-Δ transforms. The complete graph
K6 is also in the Petersen family. These graphs form the forbidden minors for linklessly embeddable graphs
, graphs that can be embedded into three-dimensional space in such a way that no two cycles in the graph are linked
.
The Clebsch graph
contains many copies of the Petersen graph as induced subgraphs: for each vertex v of the Clebsch graph, the ten non-neighbors of v induce a copy of the Petersen graph.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen
Julius Petersen
Julius Peter Christian Petersen was a Danish mathematician.-Biography:Petersen's interests in mathematics were manifold .His famous paper Die Theorie der regulären graphs was a fundamental...
, who in 1898 constructed it to be the smallest bridgeless
Bridge (graph theory)
In graph theory, a bridge is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle....
cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
with no three-edge-coloring. Although the graph is generally credited to Petersen, it had in fact first appeared 12 years earlier, in a paper by .
Donald Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
states that the Petersen graph is "a remarkable configuration that serves as a counterexample to many optimistic predictions about what might be true for graphs in general."
Constructions
The Petersen graph is the complementComplement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of the line graph
Line graph
In graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...
of
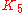. It is also the Kneser graphKneser graph
In graph theory, the Kneser graph is the graph whose vertices correspond to the -element subsets of a set of elements, and where two vertices are connected if and only if the two corresponding sets are disjoint...
; this means that it has one vertex for each 2-element subset of a 5-element set, and two vertices are connected by an edge if and only if the corresponding 2-element subsets are disjoint from each other. As a Kneser graph of the form 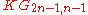it is an example of an odd graphOdd graph
In the mathematical field of graph theory, the odd graphs On are a family of symmetric graphs with high odd girth, defined from certain set systems. They include and generalize the Petersen graph.-Definition and examples:...
.
Geometrically, the Petersen graph is the graph formed by the vertices and edges of the hemi-dodecahedron
Hemi-dodecahedron
A hemi-dodecahedron is an abstract regular polyhedron, containing half the faces of a regular dodecahedron. It can be realized as a projective polyhedron , which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and...
, that is, a dodecahedron with opposite points, lines and faces identified together.
Embeddings
The Petersen graph is nonplanarPlanar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
. Any nonplanar graph has as minor
Minor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
s either the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
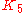, or the complete bipartite graphComplete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
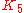, but the Petersen graph has both as minors. The minor can be formed by contracting the edges of a perfect matching, for instance the five short edges in the first picture. The minor can be formed by deleting one vertex (for instance the central vertex of the 3-symmetric drawing) and contracting an edge incident to each neighbor of the deleted vertex.Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
the Petersen graph can be drawn without edge crossings; it therefore has orientable genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
1.
Unit distance graph
In mathematics, and particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points by an edge whenever the distance between the two points is exactly one...
.
The simplest non-orientable surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
on which the Petersen graph can be embedded without crossings is the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
. This is the embedding given by the hemi-dodecahedron
Hemi-dodecahedron
A hemi-dodecahedron is an abstract regular polyhedron, containing half the faces of a regular dodecahedron. It can be realized as a projective polyhedron , which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and...
construction of the Petersen graph. The projective plane embedding can also be formed from the standard pentagonal drawing of the Petersen graph by placing a cross-cap
Cross-cap
In mathematics, a cross-cap is a two-dimensional surface that is a model of a Möbius strip with a single self intersection. This self intersection precludes the cross-cap from being topologically equivalent to a Möbius strip...
within the five-point star at the center of the drawing, and routing the star edges through this cross-cap; the resulting drawing has six pentagonal faces. This construction forms a regular map
Regular map (graph theory)
In mathematics, a regular map is a symmetric tessellation of a closed surface. More precisely, a regular map is a decomposition of a two-dimensional manifold such as a sphere, torus, or Klein bottle into topological disks, such that every flag can be transformed into any other flag by a symmetry...
and shows that the Petersen graph has non-orientable genus
Genus (mathematics)
In mathematics, genus has a few different, but closely related, meanings:-Orientable surface:The genus of a connected, orientable surface is an integer representing the maximum number of cuttings along non-intersecting closed simple curves without rendering the resultant manifold disconnected. It...
1.
Symmetries
The Petersen graph is strongly regularStrongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
(with signature srg(10,3,0,1)). It is also symmetric
Symmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
, meaning that it is edge transitive
Edge-transitive graph
In the mathematical field of graph theory, an edge-transitive graph is a graph G such that, given any two edges e1 and e2 of G, there is anautomorphism of G that maps e1 to e2....
and vertex transitive
Vertex-transitive graph
In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
. More strongly, it is 3-arc-transitive: every directed three-edge path in the Petersen graph can be transformed into every other such path by a symmetry of the graph.
It is one of only 13 cubic distance-regular graph
Distance-regular graph
In mathematics, a distance-regular graph is a regular graph such that for any two vertices v and w at distance i the number of vertices adjacent to w and at distance j from v is the same. Every distance-transitive graph is distance-regular...
s.
The automorphism group
Graph automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....
of the Petersen graph is the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
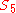; the action of 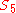on the Petersen graph follows from its construction as a Kneser graphKneser graph
In graph theory, the Kneser graph is the graph whose vertices correspond to the -element subsets of a set of elements, and where two vertices are connected if and only if the two corresponding sets are disjoint...
. Every homomorphism
Graph homomorphism
In the mathematical field of graph theory a graph homomorphism is a mapping between two graphs that respects their structure. More concretely it maps adjacent vertices to adjacent vertices.-Definitions:...
of the Petersen graph to itself that doesn't identify adjacent vertices is an automorphism. As shown in the figures, the drawings of the Petersen graph may exhibit five-way or three-way symmetry, but it is not possible to draw the Petersen graph in the plane in such a way that the drawing exhibits the full symmetry group of the graph.
Despite its high degree of symmetry, the Petersen graph is not a Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
. It is the smallest vertex-transitive graph that is not a Cayley graph.
Hamiltonian paths and cycles
The Petersen graph has a Hamiltonian pathHamiltonian path
In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected graph that visits each vertex exactly once. A Hamiltonian cycle is a cycle in an undirected graph that visits each vertex exactly once and also returns to the starting vertex...
but no Hamiltonian cycle. It is the smallest bridgeless cubic graph with no Hamiltonian cycle. It is hypohamiltonian
Hypohamiltonian graph
In the mathematical field of graph theory, a graph G is said to be hypohamiltonian if G does not itself have a Hamiltonian cycle but every graph formed by removing a single vertex from G is Hamiltonian.-History:...
, meaning that although it has no Hamiltonian cycle, deleting any vertex makes it Hamiltonian, and is the smallest hypohamiltonian graph.
As a finite connected vertex-transitive graph that does not have a Hamiltonian cycle, the Petersen graph is a counterexample to a variant of the Lovász conjecture
Lovász conjecture
In graph theory, the Lovász conjecture is a classical problem on Hamiltonian paths in graphs. It says:The original article of Lovász stated the result in the opposite, butthis version became standard...
, but the canonical formulation of the conjecture asks for a Hamiltonian path and is verified by the Petersen graph.
Only five vertex-transitive graphs with no Hamiltonian cycles are known: the complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
K2, the Petersen graph, the Coxeter graph
Coxeter graph
In the mathematical field of graph theory, the Coxeter graph is a 3-regular graph with 28 vertices and 42 edges. All the cubic distance-regular graphs are known. The Coxeter graph is one of the 13 such graphs....
and two graphs derived from the Petersen and Coxeter graphs by replacing each vertex with a triangle. If G is a 2-connected, r-regular graph with at most 3r + 1 vertices, then G is Hamiltonian or G is the Petersen graph.
To see that the Petersen graph has no Hamiltonian cycle C, we describe the ten-vertex 3-regular graphs
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
that do have a Hamiltonian cycle and show that none of them is the Petersen graph, by finding a cycle in each of them that is shorter than any cycle in the Petersen graph. Any ten-vertex Hamiltonian 3-regular graph consists of a ten-vertex cycle C plus five chords. If any chord connects two vertices at distance two or three along C from each other, the graph has a 3-cycle or 4-cycle, and therefore cannot be the Petersen graph. If two chords connect opposite vertices of C to vertices at distance four along C, there is again a 4-cycle. The only remaining case is a Möbius ladder
Möbius ladder
In graph theory, the Möbius ladder Mn is a cubic circulant graph with an even number n of vertices, formed from an n-cycle by adding edges connecting opposite pairs of vertices in the cycle...
formed by connecting each pair of opposite vertices by a chord, which again has a 4-cycle. Since the Petersen graph has girth five, it cannot be formed in this way and has no Hamiltonian cycle.
Coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
with three colors — but not with two — such that no edge connects vertices of the same color.
The Petersen graph has chromatic index 4; coloring the edges requires four colors. A proof of this requires checking four cases to demonstrate that no 3-edge-coloring exists. As a connected bridgeless cubic graph with chromatic index four, the Petersen graph is a snark
Snark (graph theory)
In the mathematical field of graph theory, a snark is a connected, bridgeless cubic graph with chromatic index equal to 4. In other words, it is a graph in which every vertex has three neighbors, and the edges cannot be colored by only three colors without two edges of the same color meeting at a...
. It is the smallest possible snark, and was the only known snark from 1898 until 1946. The snark theorem
Snark (graph theory)
In the mathematical field of graph theory, a snark is a connected, bridgeless cubic graph with chromatic index equal to 4. In other words, it is a graph in which every vertex has three neighbors, and the edges cannot be colored by only three colors without two edges of the same color meeting at a...
, a result conjectured by W. T. Tutte
W. T. Tutte
William Thomas Tutte, OC, FRS, known as Bill Tutte, was a British, later Canadian, codebreaker and mathematician. During World War II he made a brilliant and fundamental advance in Cryptanalysis of the Lorenz cipher, a major German code system, which had a significant impact on the Allied...
and announced in 2001 by Robertson, Sanders, Seymour, and Thomas, states that every snark has the Petersen graph as a minor
Minor (graph theory)
In graph theory, an undirected graph H is called a minor of the graph G if H is isomorphic to a graph that can be obtained by zero or more edge contractions on a subgraph of G....
.
Additionally, the graph has fractional chromatic index 3, proving that the difference between the chromatic index and fractional chromatic index can be as large as 1. The long-standing Goldberg-Seymour Conjecture proposes that this is the largest gap possible.
The Thue number
Thue number
In the mathematical area of graph theory, the Thue number of a graph is a variation of the chromatic index, defined by Alon et al. and named by them after mathematician Axel Thue, who studied the squarefree words used to define this number.Alon et al...
(a variant of the chromatic index) of the Petersen graph is 5.
Other properties
The Petersen graph:- is 3-connected and hence 3-edge-connected and bridgeless. See the glossary.
- has independence number 4 and is 3-partite. See the glossary.
- is cubicCubic graphIn the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
, has domination number 3, and has a perfect matching and a 2-factor. - is the smallest cubic graph of girth 5. (It is the unique
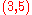-cageCage (graph theory)In the mathematical area of graph theory, a cage is a regular graph that has as few vertices as possible for its girth.Formally, an -graph is defined to be a graph in which each vertex has exactly r neighbors, and in which the shortest cycle has length exactly g. It is known that an -graph exists...
. In fact, since it has only 10 vertices, it is the unique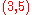
-Moore graph.) - has radius 2 and diameter 2. It is the largest cubic graph with diameter 2.
- has graph spectrumSpectral graph theoryIn mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
−2, −2, −2, −2, 1, 1, 1, 1, 1, 3. - has 2000 spanning treeSpanning tree (mathematics)In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
s, the most of any 10-vertex cubic graph. - has chromatic polynomialChromatic polynomialThe chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...
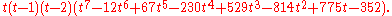
- has characteristic polynomialCharacteristic polynomialIn linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....
, making it an integral graphIntegral graphIn the mathematical field of graph theory, an integral graph is a graph whose spectrum consists entirely of integers. In other words, a graphs is an integral graph if all the eigenvalues of its characteristic polynomial are integers....
—a graph whose spectrumSpectral graph theoryIn mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
consists entirely of integers.
Related graphs
The generalized Petersen graphGeneralized Petersen graph
In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized...
G(n,k) is formed by connecting the vertices of a regular n-gon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
to the corresponding vertices of a star polygon with Schläfli symbol {n/k}. For instance, in this notation, the Petersen graph is G(5,2): it can be formed by connecting corresponding vertices of a pentagon and five-point star, and the edges in the star connect every second vertex.
The generalized Petersen graphs also include the n-prism G(n,1)
the Dürer graph
Dürer graph
In the mathematical field of graph theory, the Dürer graph is an undirected graph with 12 vertices and 18 edges. It is named after Albrecht Dürer, whose 1514 engraving Melencolia I includes a depiction of Dürer's solid, a convex polyhedron having the Dürer graph as its skeleton...
G(6,2), the Möbius-Kantor graph
G(8,3), the dodecahedron G(10,2), the Desargues graph
Desargues graph
In the mathematical field of graph theory, the Desargues graph is a distance-transitive cubic graph with 20 vertices and 30 edges. It is named after Gérard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial...
G(10,3) and the Nauru graph
Nauru graph
In the mathematical field of graph theory, the Nauru graph is a symmetric bipartite cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru....
G(12,5).
The Petersen family
Petersen family
In graph theory, the Petersen family is a set of seven undirected graphs that includes the Petersen graph and the complete graph K6. The Petersen family is named after Danish mathematician Julius Petersen, the namesake of the Petersen graph....
consists of the seven graphs that can be formed from the Petersen graph by zero or more applications of Δ-Y or Y-Δ transforms. The complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
K6 is also in the Petersen family. These graphs form the forbidden minors for linklessly embeddable graphs
Linkless embedding
In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into Euclidean space in such a way that no two cycles of the graph have nonzero linking number. A flat embedding is an embedding with the property that every cycle is the...
, graphs that can be embedded into three-dimensional space in such a way that no two cycles in the graph are linked
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
.
The Clebsch graph
Clebsch graph
In the mathematical field of graph theory, the Clebsch graph is an undirected graph with 16 vertices and 40 edges. It is named after Alfred Clebsch, a German mathematician who discovered it in 1868...
contains many copies of the Petersen graph as induced subgraphs: for each vertex v of the Clebsch graph, the ten non-neighbors of v induce a copy of the Petersen graph.
External links
- Keller, Mitch.
- Petersen Graph in the On-Line Encyclopedia of Integer SequencesOn-Line Encyclopedia of Integer SequencesThe On-Line Encyclopedia of Integer Sequences , also cited simply as Sloane's, is an online database of integer sequences, created and maintained by N. J. A. Sloane, a researcher at AT&T Labs...