In the mathematical

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 area of graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, a cage is a regular graph

Regular graph

In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...

 that has as few vertices

Vertex (graph theory)

In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...

 as possible for its girth.

Formally, an (r,g)-graph is defined to be a graph in which each vertex has exactly r neighbors, and in which the shortest cycle

Cycle graph

In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...

 has length exactly g. It is known that an (r,g)-graph exists for any combination of r ≥ 2 and g ≥ 3. An (r,g)-cage is an (r,g)-graph with the fewest possible number of vertices, among all (r,g)-graphs.

If a Moore graph exists with degree r and girth g, it must be a cage. Moreover, the bounds on the sizes of Moore graphs generalize to cages: any cage with odd girth g must have at least

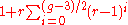
vertices, and any cage with even girth g must have at least

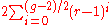
vertices. Any (r,g)-graph with exactly this many vertices is by definition a Moore graph and therefore automatically a cage.

There may exist multiple cages for a given combination of r and g. For instance there are three nonisomorphic (3,10)-cages, each with 70 vertices : the Balaban 10-cage

Balaban 10-cage

In the mathematical field of graph theory, the Balaban 10-cage or Balaban -cage is a 3-regular graph with 70 vertices and 105 edges named after A. T. Balaban. Published in 1972, It was the first -cage discovered but is not unique....

, the Harries graph

Harries graph

In the mathematical field of graph theory, the Harries graph or Harries -cage is a 3-regular undirected graph with 70 vertices and 105 edges....

 and the Harries-Wong graph. But there is only one (3,11)-cage : the Balaban 11-cage

Balaban 11-cage

In the mathematical field of graph theory, the Balaban 11-cage or Balaban -cage is a 3-regular graph with 112 vertices and 168 edges named after A. T. Balaban.The Balaban 11-cage is the unique -cage. It was discovered by Balaban in 1973...

 (with 112 vertices).

Known cages

A degree-one graph has no cycle, and a connected degree-two graph has girth equal to its number of vertices, so cages are only of interest for r ≥ 3. The (r,3)-cage is a complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

 K_r+1 on r+1 vertices, and the (r,4)-cage is a complete bipartite graph

Complete bipartite graph

In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...

 K_r,r on 2r vertices.

Other notable cages include the Moore graphs:

• (3,5)-cage: the Petersen graph
  Petersen graph
  In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
  
  , 10 vertices
• (3,6)-cage: the Heawood graph
  Heawood graph
  In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.-Combinatorial properties:...
  
  , 14 vertices
• (3,8)-cage: the Tutte–Coxeter graph, 30 vertices
• (3,10)-cage: the Balaban 10-cage
  Balaban 10-cage
  In the mathematical field of graph theory, the Balaban 10-cage or Balaban -cage is a 3-regular graph with 70 vertices and 105 edges named after A. T. Balaban. Published in 1972, It was the first -cage discovered but is not unique....
  
  , 70 vertices
• (7,5)-cage: The Hoffman–Singleton graph, 50 vertices.

The numbers of vertices in the known (r,g) cages, for values of r > 2 and g > 2 are:

g:	3	4	5	6	7	8	9	10	11	12
r = 3:	4	6	10	14	24	30	58	70	112	126
r = 4:	5	8	19	26	67	80				728
r = 5:	6	10	30	42		170				2730
r = 6:	7	12	40	62		312				7812
r = 7:	8	14	50	90

External links

• Brouwer, Andries E.
  Andries Brouwer
  Andries Evert Brouwer is a Dutch mathematician and computer programmer, a professor at Eindhoven University of Technology . His varied research interests include several branches of discrete mathematics, particularly graph theory and coding theory...
  
  Cages

• Royle, Gordon. Cubic Cages and Higher valency cages