
Complete graph
Unanswered Questions
Discussions
Encyclopedia
{infobox graph
| name = Complete graph
| image =
| image_caption = , a complete graph with 7 vertices
| vertices =
| diameter = 1
| girth =
| edges =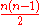
|notation =
| automorphisms =
| chromatic_number =
| chromatic_index = if is odd
if is even
| spectrum = {(-1)1, -1-1}
| properties =
In the mathematical
field of graph theory
, a complete graph is a simple undirected graph in which every pair of distinct vertices
is connected by a unique edge.
), and is denoted by (from the German komplett). It is a regular graph
of degree
. All complete graphs are their own maximal cliques
. They are maximally connected
as the only vertex cut which disconnects the graph is the complete set of vertices. The complement graph
of a complete graph is an empty graph.
If the edges of a complete graph are each given an orientation, the resulting directed graph
is called a tournament
.
. Geometrically forms the edge set of a triangle
, a tetrahedron
, etc. The Császár polyhedron
, a nonconvex polyhedron with the topology of a torus
, has the complete graph as its skeleton. Every neighborly polytope
in four or more dimensions also has a complete skeleton.
through are all planar graph
s. However, every planar drawing of a complete graph with five or more vertices must contain a crossing, and the nonplanar complete graph plays a key role in the characterizations of planar graphs: by Kuratowski's theorem, a graph is planar if and only if it contains neither nor the complete bipartite graph
as a subdivision, and by Wagner's theorem the same result holds for graph minors in place of subdivisions. As part of the Petersen family
, plays a similar role as one of the forbidden minors for linkless embedding
.
| name = Complete graph
| image =

| image_caption = , a complete graph with 7 vertices
| vertices =
| diameter = 1
| girth =

| edges =
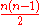
|notation =
| automorphisms =
| chromatic_number =
| chromatic_index = if is odd
if is even
| spectrum = {(-1)1, -1-1}
| properties =
In the mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a complete graph is a simple undirected graph in which every pair of distinct vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
is connected by a unique edge.
Properties
The complete graph on vertices has edges (a triangular numberTriangular number
A triangular number or triangle number numbers the objects that can form an equilateral triangle, as in the diagram on the right. The nth triangle number is the number of dots in a triangle with n dots on a side; it is the sum of the n natural numbers from 1 to n...
), and is denoted by (from the German komplett). It is a regular graph
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
of degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
. All complete graphs are their own maximal cliques
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
. They are maximally connected
Connectivity (graph theory)
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements which need to be removed to disconnect the remaining nodes from each other. It is closely related to the theory of network flow problems...
as the only vertex cut which disconnects the graph is the complete set of vertices. The complement graph
Complement graph
In graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the complement of a graph, one fills in all the missing edges required to form a complete graph, and...
of a complete graph is an empty graph.
If the edges of a complete graph are each given an orientation, the resulting directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
is called a tournament
Tournament (graph theory)
A tournament is a directed graph obtained by assigning a direction for each edge in an undirected complete graph. That is, it is a directed graph in which every pair of vertices is connected by a single directed edge....
.
Geometry and topology
A complete graph with nodes represents the edges of an -simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
. Geometrically forms the edge set of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
, a tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, etc. The Császár polyhedron
Császár polyhedron
In geometry, the Császár polyhedron is a nonconvex polyhedron, topologically a toroid, with 14 triangular faces.This polyhedron has no diagonals; every pair of vertices is connected by an edge. The seven vertices and 21 edges of the Császár polyhedron form an embedding of the complete graph K_7...
, a nonconvex polyhedron with the topology of a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
, has the complete graph as its skeleton. Every neighborly polytope
Neighborly polytope
In geometry and polyhedral combinatorics, a k-neighborly polytope is a convex polytope in which every set of k or fewer vertices forms a face. For instance, a 2-neighborly polytope is a polytope in which every pair of vertices is connected by an edge, forming a complete graph...
in four or more dimensions also has a complete skeleton.
through are all planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
s. However, every planar drawing of a complete graph with five or more vertices must contain a crossing, and the nonplanar complete graph plays a key role in the characterizations of planar graphs: by Kuratowski's theorem, a graph is planar if and only if it contains neither nor the complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
as a subdivision, and by Wagner's theorem the same result holds for graph minors in place of subdivisions. As part of the Petersen family
Petersen family
In graph theory, the Petersen family is a set of seven undirected graphs that includes the Petersen graph and the complete graph K6. The Petersen family is named after Danish mathematician Julius Petersen, the namesake of the Petersen graph....
, plays a similar role as one of the forbidden minors for linkless embedding
Linkless embedding
In topological graph theory, a mathematical discipline, a linkless embedding of an undirected graph is an embedding of the graph into Euclidean space in such a way that no two cycles of the graph have nonzero linking number. A flat embedding is an embedding with the property that every cycle is the...
.
Examples
Complete graphs on vertices, for between 1 and 12, are shown below along with the numbers of edges:  |
 |
 |
|

