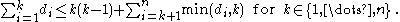Degree (graph theory)
Encyclopedia
In graph theory
, the degree (or valency) of a vertex
of a graph
is the number of edges incident to the vertex, with loop
s counted twice. The degree of a vertex is denoted
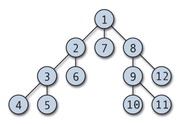
is denoted 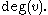 The maximum degree of a graph G, denoted by Δ(G), and the minimum degree of a graph, denoted by δ(G), are the maximum and minimum degree of its vertices. In the graph on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph
The maximum degree of a graph G, denoted by Δ(G), and the minimum degree of a graph, denoted by δ(G), are the maximum and minimum degree of its vertices. In the graph on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph
, all degrees are the same, and so we can speak of the degree of the graph.
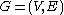 ,
,
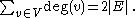
The formula implies that in any graph, the number of vertices with odd degree is even. This statement (as well as the degree sum formula) is known as the handshaking lemma
. The latter name comes from a popular mathematical problem, to prove that in any group of people the number of people who have shaken hands with an odd number of other people from the group is even.
 The degree sequence of an undirected graph is the non-increasing sequence of its vertex degrees; for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a graph invariant so isomorphic graphs
The degree sequence of an undirected graph is the non-increasing sequence of its vertex degrees; for the above graph it is (5, 3, 3, 2, 2, 1, 0). The degree sequence is a graph invariant so isomorphic graphs
have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a graph; in some cases, non-isomorphic graphs have the same degree sequence.
The degree sequence problem is the problem of finding some or all graphs with the degree sequence being a given non-increasing sequence of positive integers. (Trailing zeroes may be ignored since they are trivially realized by adding an appropriate number of isolated vertices to the graph.) A sequence which is the degree sequence of some graph, i.e. for which the degree sequence problem has a solution, is called a graphic or graphical sequence.
The problem of finding or estimating the number of graphs with a given degree sequence is a problem from the field of graph enumeration
.
As a consequence of the degree sum formula, any sequence with an odd sum, such as (3, 3, 1), cannot be realized as the degree sequence of a graph. The converse is also true: if a sequence has an even sum, it is the degree sequence of a graph. The construction of such a graph is simple: connect odd vertices in pairs, and fill with self-loops.
Often one wishes to search for simple graphs, making the degree sequence problem more challenging. Obviously the sequence (8, 4) is not the degree sequence of a simple graph, since we would have the contradiction Δ(G) > (number of vertices − 1). The sequence (3, 3, 3, 1) is also not the degree sequence of a simple graph, but in this case the reason is less obvious. Finding general criteria for degree sequences of simple graphs is a classical problem; solutions have been offered by Erdős
and Gallai
(1960), V. J. Havel
(1955) and S. L. Hakimi
(1961), S. A. Choudum and Sierksma et al. (1991).
For example, the Erdős–Gallai theorem states that a non-increasing sequence of n numbers di (for i = 1,...,n) is the degree sequence of a simple graph if and only if the sum of the sequence is even and
Havel and Hakimi proved that (d1, d2, ..., dn) is a degree sequence of a simple graph if and only if (d2 − 1, d3 − 1, ..., dd1+1 − 1, dd1+2, dd1+3, ..., dn) is. This fact leads to a simple algorithm (the Havel-Hakimi algorithm) for realizing a simple graph with a given realizable degree sequence: Begin with a graph with no edges. Maintain a list of vertices whose degree requirement has not yet been met in non-increasing order of residual degree requirement. Connect the first vertex to the next d1 vertices in this list, and then remove it from the list. Re-sort the list and repeat until all degree requirements are met.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the degree (or valency) of a vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
of a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
is the number of edges incident to the vertex, with loop
Loop (graph theory)
In graph theory, a loop is an edge that connects a vertex to itself. A simple graph contains no loops....
s counted twice. The degree of a vertex
 is denoted
is denoted 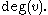 The maximum degree of a graph G, denoted by Δ(G), and the minimum degree of a graph, denoted by δ(G), are the maximum and minimum degree of its vertices. In the graph on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph
The maximum degree of a graph G, denoted by Δ(G), and the minimum degree of a graph, denoted by δ(G), are the maximum and minimum degree of its vertices. In the graph on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graphRegular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
, all degrees are the same, and so we can speak of the degree of the graph.
Handshaking lemma
The degree sum formula states that, given a graph ,
,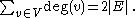
The formula implies that in any graph, the number of vertices with odd degree is even. This statement (as well as the degree sum formula) is known as the handshaking lemma
Handshaking lemma
In graph theory, a branch of mathematics, the handshaking lemma is the statement that every finite undirected graph has an even number of vertices with odd degree...
. The latter name comes from a popular mathematical problem, to prove that in any group of people the number of people who have shaken hands with an odd number of other people from the group is even.
Degree sequence

Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
have the same degree sequence. However, the degree sequence does not, in general, uniquely identify a graph; in some cases, non-isomorphic graphs have the same degree sequence.
The degree sequence problem is the problem of finding some or all graphs with the degree sequence being a given non-increasing sequence of positive integers. (Trailing zeroes may be ignored since they are trivially realized by adding an appropriate number of isolated vertices to the graph.) A sequence which is the degree sequence of some graph, i.e. for which the degree sequence problem has a solution, is called a graphic or graphical sequence.
The problem of finding or estimating the number of graphs with a given degree sequence is a problem from the field of graph enumeration
Graph enumeration
In combinatorics, an area of mathematics, graph enumeration describes a class of combinatorial enumeration problems in which one must count undirected or directed graphs of certain types, typically as a function of the number of vertices of the graph...
.
As a consequence of the degree sum formula, any sequence with an odd sum, such as (3, 3, 1), cannot be realized as the degree sequence of a graph. The converse is also true: if a sequence has an even sum, it is the degree sequence of a graph. The construction of such a graph is simple: connect odd vertices in pairs, and fill with self-loops.
Often one wishes to search for simple graphs, making the degree sequence problem more challenging. Obviously the sequence (8, 4) is not the degree sequence of a simple graph, since we would have the contradiction Δ(G) > (number of vertices − 1). The sequence (3, 3, 3, 1) is also not the degree sequence of a simple graph, but in this case the reason is less obvious. Finding general criteria for degree sequences of simple graphs is a classical problem; solutions have been offered by Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and Gallai
Tibor Gallai
Tibor Gallai was a Hungarian mathematician. He worked in combinatorics, especially in graph theory, and was a lifelong friend and collaborator of Paul Erdős. He was a student of Dénes König and an advisor of László Lovász...
(1960), V. J. Havel
V. J. Havel
V. J. Havel is a Czech mathematician known for his work with S. L. Hakimi independently on realizing a set of integers as a degree sequence of a graph. This algorithm was found out at the same time Erdős–Gallai gave their mathematical criteria.-References:...
(1955) and S. L. Hakimi
S. L. Hakimi
S. Louis Hakimi is a mathematician, a professor emeritus of mathematics at Northwestern University, IL. He is known for his work with V. J. Havel independently on realizing a set of integers as a degree sequence of a graph. This algorithm was found out at the same time Erdos-Gallai gave their...
(1961), S. A. Choudum and Sierksma et al. (1991).
For example, the Erdős–Gallai theorem states that a non-increasing sequence of n numbers di (for i = 1,...,n) is the degree sequence of a simple graph if and only if the sum of the sequence is even and
Havel and Hakimi proved that (d1, d2, ..., dn) is a degree sequence of a simple graph if and only if (d2 − 1, d3 − 1, ..., dd1+1 − 1, dd1+2, dd1+3, ..., dn) is. This fact leads to a simple algorithm (the Havel-Hakimi algorithm) for realizing a simple graph with a given realizable degree sequence: Begin with a graph with no edges. Maintain a list of vertices whose degree requirement has not yet been met in non-increasing order of residual degree requirement. Connect the first vertex to the next d1 vertices in this list, and then remove it from the list. Re-sort the list and repeat until all degree requirements are met.
Special values

- A vertex with degree 0 is called an isolated vertex.
- A vertex with degree 1 is called a leaf vertex or end vertex, and the edge incident with that vertex is called a pendant edge. In the graph on the right, {3,5} is a pendant edge. This terminology is common in the study of treeTree (graph theory)In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
s in graph theory and especially treeTree (data structure)In computer science, a tree is a widely-used data structure that emulates a hierarchical tree structure with a set of linked nodes.Mathematically, it is an ordered directed tree, more specifically an arborescence: an acyclic connected graph where each node has zero or more children nodes and at...
s as data structureData structureIn computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
s.
Global properties
- If each vertex of the graph has the same degree k the graph is called a k-regular graphRegular graphIn graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
and the graph itself is said to have degree k. - An undirected, connected graph has an Eulerian pathEulerian pathIn graph theory, an Eulerian trail is a trail in a graph which visits every edge exactly once. Similarly, an Eulerian circuit or Eulerian cycle is a Eulerian trail which starts and ends on the same vertex. They were first discussed by Leonhard Euler while solving the famous Seven Bridges of...
if and only if it has either 0 or 2 vertices of odd degree. If it has 0 vertices of odd degree, the Eulerian path is an Eulerian circuit. - A directed graph is a pseudoforestPseudoforestIn graph theory, a pseudoforest is an undirected graph in which every connected component has at most one cycle. That is, it is a system of vertices and edges connecting pairs of vertices, such that no two cycles of consecutive edges share any vertex with each other, nor can any two cycles be...
if and only if every vertex has outdegree at most 1. A functional graph is a special case of a pseudoforest in which every vertex has outdegree exactly 1. - By Brooks' theorem, any graph other than a clique or an odd cycle has chromatic number at most Δ, and by Vizing's theorem any graph has chromatic index at most Δ + 1.
- A k-degenerate graphDegeneracy (graph theory)In graph theory, a k-degenerate graph is an undirected graph in which every subgraph has a vertex of degree at most k: that is, some vertex in the subgraph touches k or fewer of the subgraph's edges. The degeneracy of a graph is the smallest value of k for which it is k-degenerate...
is a graph in which each subgraph has a vertex of degree at most k.
See also
- Indegree, outdegree for digraphs
- Degree distributionDegree distributionIn the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network.-Definition:...