Graph enumeration
Encyclopedia

Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, an area of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, graph enumeration describes a class of combinatorial enumeration problems in which one must count undirected or directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
s of certain types, typically as a function of the number of vertices of the graph. The pioneers in this area of mathematics were Polya, Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
and Redfield.
In some graphical enumeration problems, the vertices of the graph are considered to be labeled in such a way as to be distinguishable from each other, while in other problems any permutation of the vertices is considered to form the same graph. In general, labeled problems tend to be easier to solve than unlabeled problems. As with combinatorial enumeration more generally, the Pólya enumeration theorem
Pólya enumeration theorem
The Pólya enumeration theorem , also known as the Redfield–Pólya Theorem, is a theorem in combinatorics that both follows and ultimately generalizes Burnside's lemma on the number of orbits of a group action on a set. The theorem was first published by John Howard Redfield in 1927...
is an important tool for dealing with symmetries such as this.
Some important results in this area include the following.
- The number of labeled n-vertex undirected graphs is 2n(n − 1)/2.
- The number of labeled n-vertex directed graphs is 2n(n − 1).
- The number Cn of connected labeled n-vertex undirected graphs satisfies the recurrence relationRecurrence relationIn mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
-
- from which one may easily calculate, for n = 1, 2, 3, ..., that the values for Cn are
- 1, 1, 4, 38, 728, 26704, 1866256, ...
- The number of labeled n-vertex free trees is nn − 2 (Cayley's formula).
- The number of unlabeled n-vertex caterpillarsCaterpillar treeIn graph theory, a caterpillar or caterpillar tree is a tree in which all the vertices of the caterpillar are within distance 1 of a central path....
is
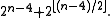
- 1, 1, 4, 38, 728, 26704, 1866256, ...