Regular graph
Encyclopedia
In graph theory
, a regular graph is a graph
where each vertex has the same number of neighbors; i.e. every vertex has the same degree
or valency. A regular directed graph
must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other. A regular graph with vertices of degree k is called a k‑regular graph or regular graph of degree k.
Regular graphs of degree at most 2 are easy to classify: A 0-regular graph consists of disconnected vertices, a 1-regular graph consists of disconnected edges, and a 2-regular graph consists of disconnected cycle
s.
A 3-regular graph is known as a cubic graph
.
A strongly regular graph
is a regular graph where every adjacent pair of vertices has the same number l of neighbors in common, and every non-adjacent pair of vertices has the same number n of neighbors in common. The smallest graphs that are regular but not strongly regular are the cycle graph
and the circulant graph
on 6 vertices.
The complete graph
is strongly regular for any 
.
A theorem by Nash-Williams
says that every k‑regular graph on 2k + 1 vertices has a Hamiltonian cycle.
of a graph. Then the graph is regular if and only if
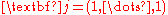is an eigenvector of A. Its eigenvalue will be the constant degree of the graph. Eigenvectors corresponding to other eigenvalues are orthogonal to 
, so for such eigenvectors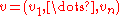 
, we have 
.
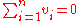A regular graph of degree k is connected if and only if the eigenvalue k has multiplicity one.
There is also a criterion for regular and connected graphs :
a graph is connected and regular if and only if the matrix J, with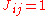
, is in the adjacency algebra
of the graph (meaning it is a linear combination of powers of A).
Let G be a k-regular graph with diameter D and eigenvalues of adjacency matrix
. If G is not bipartite
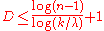
where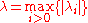
.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a regular graph is a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
where each vertex has the same number of neighbors; i.e. every vertex has the same degree
Degree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
or valency. A regular directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other. A regular graph with vertices of degree k is called a k‑regular graph or regular graph of degree k.
Regular graphs of degree at most 2 are easy to classify: A 0-regular graph consists of disconnected vertices, a 1-regular graph consists of disconnected edges, and a 2-regular graph consists of disconnected cycle
Cycle (graph theory)
In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...
s.
A 3-regular graph is known as a cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
.
A strongly regular graph
Strongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
is a regular graph where every adjacent pair of vertices has the same number l of neighbors in common, and every non-adjacent pair of vertices has the same number n of neighbors in common. The smallest graphs that are regular but not strongly regular are the cycle graph
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
and the circulant graph
Circulant graph
In graph theory, a circulant graph is an undirected graph that has a cyclic group of symmetries that includes a symmetry taking any vertex to any other vertex.-Equivalent definitions:Circulant graphs can be described in several equivalent ways:...
on 6 vertices.
The complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
is strongly regular for any .A theorem by Nash-Williams
Crispin St. J. A. Nash-Williams
Crispin St. John Alvah Nash-Williams was a British and Canadian mathematician. His research interest was in the field of discrete mathematics, especially graph theory....
says that every k‑regular graph on 2k + 1 vertices has a Hamiltonian cycle.
Algebraic properties
Let A be the adjacency matrixAdjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
of a graph. Then the graph is regular if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
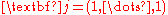is an eigenvector of A. Its eigenvalue will be the constant degree of the graph. Eigenvectors corresponding to other eigenvalues are orthogonal to , so for such eigenvectors 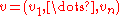, we have 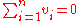.A regular graph of degree k is connected if and only if the eigenvalue k has multiplicity one.
There is also a criterion for regular and connected graphs :
a graph is connected and regular if and only if the matrix J, with
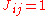, is in the adjacency algebraAdjacency algebra
In algebraic graph theory, the adjacency algebra of a graph G is the algebra of polynomials in the adjacency matrix A of the graph...
of the graph (meaning it is a linear combination of powers of A).
Let G be a k-regular graph with diameter D and eigenvalues of adjacency matrix
. If G is not bipartite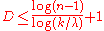where
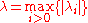.See also
- Random regular graph
- Strongly regular graphStrongly regular graphIn graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
- Moore graph
- Cage graph
External links
- GenReg software and data by Markus Meringer.