In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, a circulant graph is an undirected graph that has a cyclic group

Cyclic group

In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...

 of symmetries

Graph automorphism

In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....

 that includes a symmetry taking any vertex to any other vertex

Vertex-transitive graph

In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...

.

Equivalent definitions

Circulant graphs can be described in several equivalent ways:

• The automorphism group of the graph includes a cyclic
  Cyclic group
  In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
  
   subgroup
  Subgroup
  In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
  
   that acts transitively
  Group action
  In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
  
   on the graph's vertices.
• The graph has an adjacency matrix
  Adjacency matrix
  In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
  
   that is a circulant matrix
  Circulant matrix
  In linear algebra, a circulant matrix is a special kind of Toeplitz matrix where each row vector is rotated one element to the right relative to the preceding row vector. In numerical analysis, circulant matrices are important because they are diagonalized by a discrete Fourier transform, and hence...
  
  .
• The vertices of the graph can be numbered from 0 to in such a way that, if some two vertices numbered and are adjacent, then every two vertices numbered and are adjacent.
• The graph can be drawn (possibly with crossings) so that its vertices lie on the corners of a regular polygon, and every rotational symmetry of the polygon is also a symmetry of the drawing. (However, reflecting the polygon may give a different drawing.)

• The circulant graph with jumps is often defined as the graph with nodes labeled each node being adjacent to the nodes .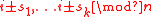

Examples

Every cycle graph

Cycle graph

In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...

 is a circulant graph, as is every crown graph

Crown graph

In graph theory, a branch of mathematics, a crown graph on 2n vertices is an undirected graph with two sets of vertices ui and vi and with an edge from ui to vj whenever i ≠ j...

.

The Paley graph

Paley graph

In mathematics, and specifically graph theory, Paley graphs, named after Raymond Paley, are dense undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ in a quadratic residue. The Paley graphs form an infinite family of conference...

s of order (where is a prime number

Prime number

A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...

 congruent to ) is a graph in which the vertices are the numbers from 0 to and two vertices are adjacent if their difference is a quadratic residue modulo . Since the presence or absence of an edge depends only on the difference modulo  of two vertex numbers, any Paley graph is a circulant graph.

Every Möbius ladder

Möbius ladder

In graph theory, the Möbius ladder Mn is a cubic circulant graph with an even number n of vertices, formed from an n-cycle by adding edges connecting opposite pairs of vertices in the cycle...

 is a circulant graph, as is every complete graph

Complete graph

In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...

. A complete bipartite graph

Complete bipartite graph

In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...

 is a circulant graph if it has the same number of vertices on both sides of its bipartition.

If two numbers and are relatively prime, then the rook's graph

Rook's graph

In graph theory, a rook's graph is a graph that represents all legal moves of the rook chess piece on a chessboard: each vertex represents a square on a chessboard and each edge represents a legal move...

 (a graph that has a vertex for each square of an chessboard and an edge for each two squares that a chess rook can move between in a single move) is a circulant graph. This is because its symmetries include as a subgroup the cyclic group . More generally, in this case, the tensor product of graphs

Tensor product of graphs

In graph theory, the tensor product G × H of graphs G and H is a graph such that* the vertex set of G × H is the Cartesian product V × V; and...

 between any - and -vertex circulants is itself a circulant.

Many of the known lower bounds on Ramsey numbers come from examples of circulant graphs that have small maximum cliques and small maximum independent sets.

Properties

From the last definiton it follows that is a 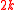regular graph. is connected if and only if 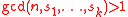. It is known that if are fixed integers then the number of spanning tree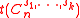s is where 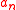satisfies a recurrence relation of order 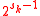. This fact can be used to derived the well known identity 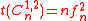where 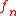denotes the n'th Fibonacci number

Fibonacci number

In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....

.

Self-complementary circulants

A self-complementary graph

Self-complementary graph

A self-complementary graph is a graph which is isomorphic to its complement. The simplest non-trivial self-complementary graphs are the 4-vertex path graph and the 5-vertex cycle graph....

 is a graph in which replacing every edge by a non-edge and vice versa produces an isomorphic

Graph isomorphism

In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...

 graph.
For instance, a five-vertex cycle graph is self-complementary, and is also a circulant graph. More generally every Paley graph

Paley graph

In mathematics, and specifically graph theory, Paley graphs, named after Raymond Paley, are dense undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ in a quadratic residue. The Paley graphs form an infinite family of conference...

 is a self-complementary circulant graph. Horst Sachs

Horst Sachs

Horst Sachs is a German mathematician, an expert in graph theory, a recipient of the Euler Medal .He earned the degree of Doctor of Science from the Martin-Luther-Universität Halle-Wittenberg in 1958...

 showed that, if a number has the property that every prime factor of must be congruent to , then there exists a self-complementary circulant with vertices. He conjectured that this condition is also necessary: that no other values of allow a self-complementary circulant to exist. The conjecture was proven some 40 years later, by Vilfred.

Ádam's conjecture

Define a circulant numbering of a circulant graph to be a labeling of the vertices of the graph by the numbers from 0 to in such a way that, if some two vertices numbered and are adjacent, then every two vertices numbered and are adjacent. Equivalently, a circulant numbering is a numbering of the vertices for which the adjacency matrix of the graph is a circulant matrix.

Let be an integer that is relatively prime to , and let be any integer. Then the linear function

Linear function

In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....

that takes a number to transforms a circulant numbering to another circulant numbering. Ádam conjectured that these linear maps are the only ways of renumbering a circulant graph while preserving the circulant property: that is, if and are isomorphic circulant graphs, with different numberings, then there is a linear map that transforms the numbering for into the numbering for . However, Ádam's conjecture is now known to be false. A counterexample is given by graphs and with 16 vertices each; a vertex in is connected to the six neighbors , , and , while in the six neighbors are , , and . These two graphs are isomorphic, but their isomorphism cannot be realized by a linear map.