Linear function
Encyclopedia
In mathematics
, the term linear function can refer to either of two different but related concepts:
In analytic geometry
, the term linear function is sometimes used to mean a first-degree polynomial
function
of one variable. These functions are known as "linear" because they are precisely the functions whose graph
in the Cartesian coordinate plane is a straight line.
Such a function can be written as
(called slope-intercept form), where
and 
are real
constants
and
is a real variable. The constant 
is often called the slope
or gradient, while
is the y-intercept
, which gives the point of intersection between the graph of the function and the
-axis. Changing 
makes the line steeper or shallower, while changing 
moves the line up or down.
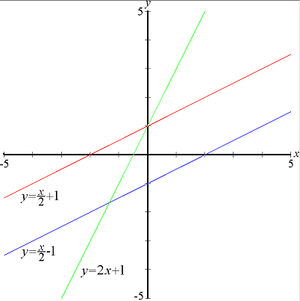
Examples of functions whose graph is a line include the following:
The graphs of these are shown in the image at right.
that is a linear map, that is, a map between two vector space
s that preserves vector addition and scalar multiplication
.
For example, if
and 
are represented as coordinate vector
s, then the linear functions are those functions
that can be expressed as
where M is a matrix
. A function
is a linear map if and only if
= 0. For other values of 
this falls in the more general class of affine maps.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the term linear function can refer to either of two different but related concepts:
- a first-degree polynomial function of one variable;
- a map between two vector spaces that preserves vector addition and scalar multiplication.
Analytic geometry
In analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
, the term linear function is sometimes used to mean a first-degree polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of one variable. These functions are known as "linear" because they are precisely the functions whose graph
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
in the Cartesian coordinate plane is a straight line.
Such a function can be written as
(called slope-intercept form), where
and are realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
constants
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
and
is a real variable. The constant is often called the slopeSlope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
or gradient, while
is the y-interceptY-intercept
In coordinate geometry, using the common convention that the horizontal axis represents a variable x and the vertical axis represents a variable y, a y-intercept is a point where the graph of a function or relation intersects with the y-axis of the coordinate system...
, which gives the point of intersection between the graph of the function and the
-axis. Changing makes the line steeper or shallower, while changing moves the line up or down.Examples of functions whose graph is a line include the following:
The graphs of these are shown in the image at right.
Vector spaces
In advanced mathematics, a linear function means a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that is a linear map, that is, a map between two vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s that preserves vector addition and scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
.
For example, if
and are represented as coordinate vectorCoordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
s, then the linear functions are those functions
that can be expressed aswhere M is a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
. A function
is a linear map if and only if
= 0. For other values of this falls in the more general class of affine maps.See also
- Nonlinear system
- Piecewise linear function
- Linear interpolationLinear interpolationLinear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...
- Discontinuous linear mapDiscontinuous linear mapIn mathematics, linear maps form an important class of "simple" functions which preserve the algebraic structure of linear spaces and are often used as approximations to more general functions . If the spaces involved are also topological spaces , then it makes sense to ask whether all linear maps...