Coordinate vector
Encyclopedia
In linear algebra
, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space
Fn.
Coordinate vectors allow calculations with abstract objects to be transformed into calculations with blocks of numbers (matrices
, column vectors and row vectors).
The idea of a coordinate vector can also be used for infinite dimensional vector spaces, as addressed below.
of dimension
n over a field
F and let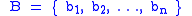
be an ordered basis for V.
Then for every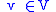
there is a unique linear combination
of the basis vectors that equals v: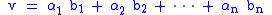
The linear independence
of vectors in the basis ensures that the α-s are determined uniquely by v and B.
Now, we define the coordinate vector of v relative to B to be the following sequence
of coordinates: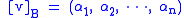
This is also called the representation of v with respect of B, or the B representation of v. The α-s are called the coordinates of v. The order of the basis becomes important here, since it determines the order in which the coefficients are listed in the coordinate vector.
Coordinate vectors of finite dimensional vector spaces can be represented as elements of a column or row vector. This depends on the author's intention of preforming linear transformation
s by matrix multiplication
on the left (pre-multiplication) or on the right (post-multiplication) of the vector. A column vector of length n can be pre-multiplied by any matrix with n columns, while a row vector of length n can be post-multiplied by any matrix with n rows.
For instance, a transformation from basis B to basis C may be obtained by pre-multiplying the column vector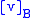
by a square matrix 
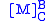(see below), resulting in a column vector 
:
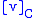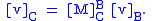
If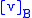
is a row vector instead of a column vector, the same basis transformation can be obtained by post-multiplying the row vector by the transposed matrix 
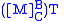to obtain the row vector 
:
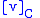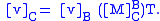
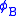, called the standard representation of V with respect to B, that takes every vector to its coordinate representation: 
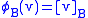. Then 
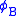is a linear transformation from V to Fn. In fact, it is an isomorphism
, and its inverse
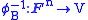is simply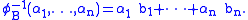
Alternatively, we could have defined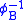
to be the above function from the beginning, realized that 
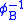is an isomorphism, and defined 
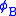to be its inverse.
matching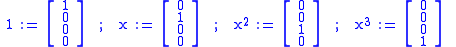
then the corresponding coordinate vector to the polynomial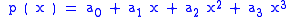
is 
.
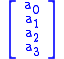According to that representation, the differentiation operator d/dx which we shall mark D will be represented by the following matrix: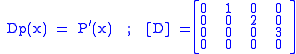
Using that method it is easy to explore the properties of the operator: such as invertibility, hermitian or anti-hermitian or none
, spectrum and eigenvalues and more.
which represent the spin
operator when transforming the spin eigenstates into vector coordinates.
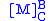the matrix
which has columns consisting of the C representation of basis vectors b1, b2, ..., bn: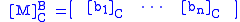
This matrix is referred to as the basis transformation matrix from B to C, and can be used for transforming any vector v from a B representation to a C representation, according to the following theorem
:
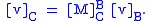
If E is the standard basis
, the transformation from B to E can be represented with the following simplified notation:
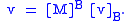
where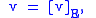
and
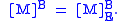
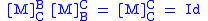
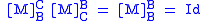
The linear transformations between (possibly) infinite dimensional vector spaces can be modeled, analogously to the finite dimensional case, with infinite matrices. The special case of the transformations from V into V is described in the full linear ring article.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space
Coordinate space
In mathematics, specifically in linear algebra, the coordinate space, Fn, is the prototypical example of an n-dimensional vector space over a field F. It can be defined as the product space of F over a finite index set.-Definition:...
Fn.
Coordinate vectors allow calculations with abstract objects to be transformed into calculations with blocks of numbers (matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, column vectors and row vectors).
The idea of a coordinate vector can also be used for infinite dimensional vector spaces, as addressed below.
Definition
Let V be a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
n over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
F and let
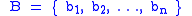
be an ordered basis for V.
Then for every
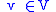there is a unique linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the basis vectors that equals v:
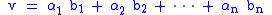
The linear independence
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
of vectors in the basis ensures that the α-s are determined uniquely by v and B.
Now, we define the coordinate vector of v relative to B to be the following sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of coordinates:
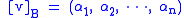
This is also called the representation of v with respect of B, or the B representation of v. The α-s are called the coordinates of v. The order of the basis becomes important here, since it determines the order in which the coefficients are listed in the coordinate vector.
Coordinate vectors of finite dimensional vector spaces can be represented as elements of a column or row vector. This depends on the author's intention of preforming linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
s by matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
on the left (pre-multiplication) or on the right (post-multiplication) of the vector. A column vector of length n can be pre-multiplied by any matrix with n columns, while a row vector of length n can be post-multiplied by any matrix with n rows.
For instance, a transformation from basis B to basis C may be obtained by pre-multiplying the column vector
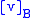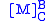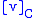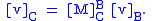
by a square matrix (see below), resulting in a column vector :If
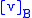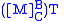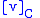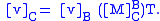
is a row vector instead of a column vector, the same basis transformation can be obtained by post-multiplying the row vector by the transposed matrix to obtain the row vector :The standard representation
We can mechanize the above transformation by defining a function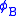, called the standard representation of V with respect to B, that takes every vector to its coordinate representation: 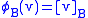. Then 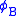is a linear transformation from V to Fn. In fact, it is an isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
, and its inverse
Inverse function
In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...
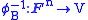is simply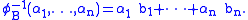Alternatively, we could have defined
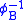to be the above function from the beginning, realized that 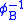is an isomorphism, and defined 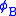to be its inverse.Example 1
Let P4 be the space of all the algebraic polynomials in degree less than 4 (i.e. the highest exponent of x can be 3). This space is linear and spanned by the following polynomials:matching
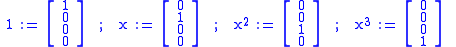
then the corresponding coordinate vector to the polynomial
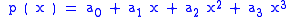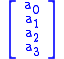is .According to that representation, the differentiation operator d/dx which we shall mark D will be represented by the following matrix:
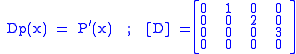
Using that method it is easy to explore the properties of the operator: such as invertibility, hermitian or anti-hermitian or none
Hermitian
A number of mathematical entities are named Hermitian, after the mathematician Charles Hermite:*Hermitian adjoint*Hermitian connection, the unique connection on a Hermitian manifold that satisfies specific conditions...
, spectrum and eigenvalues and more.
Example 2
The Pauli matricesPauli matrices
The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
which represent the spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
operator when transforming the spin eigenstates into vector coordinates.
Basis transformation matrix
Let B and C be two different bases of a vector space V, and let us mark with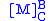 the matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
which has columns consisting of the C representation of basis vectors b1, b2, ..., bn:
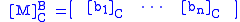
This matrix is referred to as the basis transformation matrix from B to C, and can be used for transforming any vector v from a B representation to a C representation, according to the following theorem
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
:
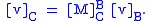
If E is the standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
, the transformation from B to E can be represented with the following simplified notation:
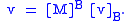
where
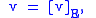and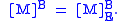Corollary
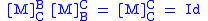
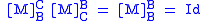
The matrix M is an invertible matrix and M-1 is the basis transformation matrix from C to B. In other words,Remarks
- The basis transformation matrix can be regarded as an automorphismAutomorphismIn mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
over V. - In order to easily remember the theorem
-
-
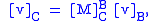
- notice that M 's superscript and v 's subscript indices are "canceling" each other and M 's subscript becomes v 's new subscript. This "canceling" of indices is not a real canceling but rather a convenient and intuitively appealing, although mathematically incorrect, manipulation of symbols, permitted by an appropriately chosen notation.
-
Infinite dimensional vector spaces
Suppose V is an infinite dimensional vector space over a field F. If the dimension is κ, then there is some basis of κ elements for V. After an order is chosen, the basis can be considered an ordered basis. The elements of V are finite linear combinations of elements in the basis, which give rise to unique coordinate representations exactly as described before. The only change is that the indexing set for the coordinates is not finite. Since a given vector v is a finite linear combination of basis elements, the only nonzero entries of the coordinate vector for v will be the nonzero coefficients of the linear combination representing v. Thus the coordinate vector for v is zero except in finitely many entries.The linear transformations between (possibly) infinite dimensional vector spaces can be modeled, analogously to the finite dimensional case, with infinite matrices. The special case of the transformations from V into V is described in the full linear ring article.