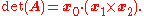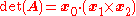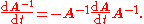Invertible matrix
Encyclopedia
In linear algebra
an n-by-n (square) matrix
A is called invertible (some authors use nonsingular or nondegenerate) if there exists an n-by-n matrix B such that
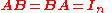
where In denotes the n-by-n identity matrix
and the multiplication used is ordinary matrix multiplication
. If this is the case, then the matrix B is uniquely determined by A and is called the inverse of A, denoted by A−1. It follows from the theory of matrices that if
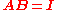
for finite square matrices A and B, then also
Non-square matrices (m-by-n matrices for which m ≠ n) do not have an inverse. However, in some cases such a matrix may have a left inverse or right inverse. If A is m-by-n and the rank
of A is equal to n, then A has a left inverse: an n-by-m matrix B such that BA = I. If A has rank m, then it has a right inverse: an n-by-m matrix B such that AB = I.
A square matrix that is not invertible is called singular or degenerate. A square matrix is singular if and only if
its determinant
is 0. Singular matrices are rare in the sense that if you pick a random square matrix, it will almost surely
not be singular.
While the most common case is that of matrices over the real
or complex
numbers, all these definitions can be given for matrices over any commutative ring
. However, in this case the condition for a square matrix to be invertible is that its determinant is invertible in the ring, which in general is a much stricter requirement than being nonzero. The conditions for existence of left-inverse resp. right-inverse are more complicated since a notion of rank does not exist over rings.
Matrix inversion is the process of finding the matrix B that satisfies the prior equation for a given invertible matrix A.
K (for example the field R of real numbers). The following statements are equivalent:
Furthermore, the following properties hold for an invertible matrix A:
A matrix that is its own inverse, i.e. A = A-1 and A2 = I, is called an involution.
, i.e., has Lebesgue
measure zero. This is true because singular matrices are the roots of the polynomial function in the entries of the matrix given by the determinant
. Thus in the language of measure theory, almost all
n-by-n matrices are invertible.
Furthermore the n-by-n invertible matrices are a dense
open set
in the topological space
of all n-by-n matrices. Equivalently, the set of singular matrices is closed
and nowhere dense in the space of n-by-n matrices.
In practice however, one may encounter non-invertible matrices. And in numerical calculations
, matrices which are invertible, but close to a non-invertible matrix, can still be problematic; such matrices are said to be ill-conditioned.
is an algorithm
that can be used to determine whether a given matrix is invertible and to find the inverse. An alternative is the LU decomposition
which generates upper and lower triangular matrices which are easier to invert. For special purposes, it may be convenient to invert matrices by treating m·n-by-m·n matrices as m-by-m matrices of n-by-n matrices, and applying one or another formula recursively (other sized matrices can be padded out with dummy rows and columns). For other purposes, a variant of Newton's method
may be convenient. Newton's method is particularly useful when dealing with families of related matrices: sometimes a good starting point for refining an approximation for the new inverse can be the already obtained inverse of a previous matrix that nearly matches the current matrix. Newton's method
is also useful for "touch up" corrections to the Gauss–Jordan algorithm
which has been contaminated by small errors due to imperfect computer arithmetic
.
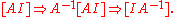
, can also be an efficient way to calculate the inverse of small matrices, but this recursive method is inefficient for large matrices. To determine the inverse, we calculate a matrix of cofactors:
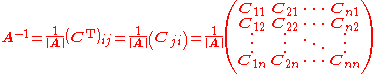
where |A| is the determinant
of A, Cij is the matrix of cofactors, and CT represents the matrix transpose
.
For most practical applications, it is not necessary to invert a matrix to solve a system of linear equations; however, for a unique solution, it is necessary that the matrix involved be invertible.
Decomposition techniques like LU decomposition
are much faster than inversion, and various fast algorithms for special classes of linear systems have also been developed.
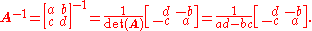
This is possible because 1/(ad-bc) is the reciprocal of the determinant of the matrix in question, and the same strategy could be used for other matrix sizes.
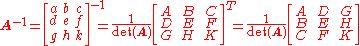
where the determinant of A can be computed by applying the rule of Sarrus
as follows:
If the determinant is non-zero, the matrix is invertible, with the elements of the above matrix on the right side given by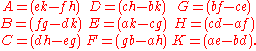
The general 3×3 inverse can be expressed concisely in terms of the cross product
and triple product
:
If a matrix
(consisting of three column vectors, 
, 
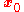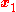, and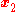 
) is invertible, its inverse is given by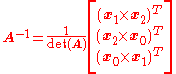
where
is a column vector and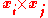 
is a row vector. Note that 
is equal to the triple product of 
, 
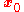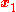, and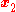 
—the volume of the parallelepiped
formed by the rows or columns:
The correctness of the formula can be checked by using cross- and triple-product properties and by noting that for groups, left and right inverses always coincide. Intuitively, because of the cross products, each row of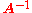
is orthogonal to the non-corresponding two columns of 
(causing the off-diagonal terms of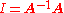 
be zero). Dividing by
causes the diagonal elements of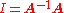
to be unity. For example, the first diagonal is: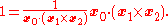
where A, B, C and D are matrix sub-blocks
of arbitrary size. (A and D must, of course, be square, so that they can be inverted. Furthermore, this is true if and only if A and D−CA−1B are nonsingular
). This strategy is particularly advantageous if A is diagonal and D−CA−1B (the Schur complement
of A) is a small matrix, since they are the only matrices requiring inversion. This technique was reinvented several times and is due to Hans Boltz (1923), who used it for the inversion of geodetic matrices, and Tadeusz Banachiewicz
(1937), who generalized it and proved its correctness.
The nullity theorem
says that the nullity of A equals the nullity of the sub-block in the lower right of the inverse matrix, and that the nullity of B equals the nullity of the sub-block in the upper right of the inverse matrix.
The inversion procedure that led to Equation (1) performed matrix block operations that operated on C and D first. Instead, if A and B are operated on first, and provided D and A−BD−1C are nonsingular
, the result is
Equating Equations (1) and (2) leads to
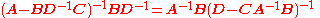
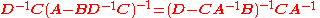
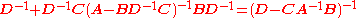
where Equation (3) is the matrix inversion lemma, which is equivalent to the binomial inverse theorem
.
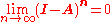
then A is nonsingular and its inverse may be expressed by a Neumann series:
Truncating the sum results in an "approximate" inverse which may be useful as a preconditioner
.
More generally, if A is "near" the invertible matrix X in the sense that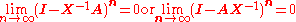
then A is nonsingular and its inverse is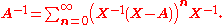
If it is also the case that A-X has rank
1 then this simplifies to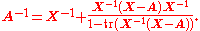
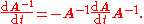
To derive the above expression for the derivative of the inverse of A, one can differentiate the definition of the matrix inverse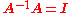
and then solve for the inverse of A:
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
an n-by-n (square) matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A is called invertible (some authors use nonsingular or nondegenerate) if there exists an n-by-n matrix B such that
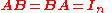
where In denotes the n-by-n identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
and the multiplication used is ordinary matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. If this is the case, then the matrix B is uniquely determined by A and is called the inverse of A, denoted by A−1. It follows from the theory of matrices that if
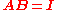
for finite square matrices A and B, then also
Non-square matrices (m-by-n matrices for which m ≠ n) do not have an inverse. However, in some cases such a matrix may have a left inverse or right inverse. If A is m-by-n and the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of A is equal to n, then A has a left inverse: an n-by-m matrix B such that BA = I. If A has rank m, then it has a right inverse: an n-by-m matrix B such that AB = I.
A square matrix that is not invertible is called singular or degenerate. A square matrix is singular if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
its determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is 0. Singular matrices are rare in the sense that if you pick a random square matrix, it will almost surely
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
not be singular.
While the most common case is that of matrices over the real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
or complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
numbers, all these definitions can be given for matrices over any commutative ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. However, in this case the condition for a square matrix to be invertible is that its determinant is invertible in the ring, which in general is a much stricter requirement than being nonzero. The conditions for existence of left-inverse resp. right-inverse are more complicated since a notion of rank does not exist over rings.
Matrix inversion is the process of finding the matrix B that satisfies the prior equation for a given invertible matrix A.
Properties
Let A be a square n by n matrix over a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K (for example the field R of real numbers). The following statements are equivalent:
- A is invertible.
- A is row-equivalent to the n-by-n identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
In. - A is column-equivalent to the n-by-n identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
In. - A has n pivot positions.
- detDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
A ≠ 0. In general, a square matrix over a commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
is invertible if and only if its determinantDeterminantIn linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is a unitUnit (ring theory)In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
in that ring. - rankRank (linear algebra)The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
A = n. - The equation Ax = 0 has only the trivial solution x = 0 (i.e., NullNull spaceIn linear algebra, the kernel or null space of a matrix A is the set of all vectors x for which Ax = 0. The kernel of a matrix with n columns is a linear subspace of n-dimensional Euclidean space...
A = {0}) - The equation Ax = b has exactly one solution for each b in Kn, (x ≠ 0).
- The columns of A are linearly independentLinear independenceIn linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
. - The columns of A span Kn (i.e. Col A = Kn).
- The columns of A form a basis of Kn.
- The linear transformation mapping x to Ax is a bijectionBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
from Kn to Kn. - There is an n by n matrix B such that AB = In = BA.
- The transposeTransposeIn linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
AT is an invertible matrix (hence rows of A are linearly independentLinear independenceIn linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
, span Kn, and form a basis of Kn). - The number 0 is not an eigenvalue of A.
- The matrix A can be expressed as a finite product of elementary matrices.
Furthermore, the following properties hold for an invertible matrix A:
- (A–1)–1 = A;
- (kA)–1 = k–1A–1 for nonzero scalar k;
- (AT)–1 = (A–1)T;
- For any invertible n-by-n matrices A and B, (AB)–1 = B–1A–1. More generally, if A1,...,Ak are invertible n-by-n matrices, then (A1A2⋯Ak–1Ak)–1 = Ak–1Ak–1–1⋯A2–1A1–1;
- det(A–1) = det(A)–1.
A matrix that is its own inverse, i.e. A = A-1 and A2 = I, is called an involution.
Density
Over the field of real numbers, the set of singular n-by-n matrices, considered as a subset of Rn×n, is a null setNull set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
, i.e., has Lebesgue
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
measure zero. This is true because singular matrices are the roots of the polynomial function in the entries of the matrix given by the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
. Thus in the language of measure theory, almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
n-by-n matrices are invertible.
Furthermore the n-by-n invertible matrices are a dense
Dense set
In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in the topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
of all n-by-n matrices. Equivalently, the set of singular matrices is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
and nowhere dense in the space of n-by-n matrices.
In practice however, one may encounter non-invertible matrices. And in numerical calculations
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, matrices which are invertible, but close to a non-invertible matrix, can still be problematic; such matrices are said to be ill-conditioned.
Gaussian elimination
Gauss–Jordan eliminationGauss–Jordan elimination
In linear algebra, Gauss–Jordan elimination is an algorithm for getting matrices in reduced row echelon form using elementary row operations. It is a variation of Gaussian elimination. Gaussian elimination places zeros below each pivot in the matrix, starting with the top row and working downwards....
is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that can be used to determine whether a given matrix is invertible and to find the inverse. An alternative is the LU decomposition
LU decomposition
In linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
which generates upper and lower triangular matrices which are easier to invert. For special purposes, it may be convenient to invert matrices by treating m·n-by-m·n matrices as m-by-m matrices of n-by-n matrices, and applying one or another formula recursively (other sized matrices can be padded out with dummy rows and columns). For other purposes, a variant of Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
may be convenient. Newton's method is particularly useful when dealing with families of related matrices: sometimes a good starting point for refining an approximation for the new inverse can be the already obtained inverse of a previous matrix that nearly matches the current matrix. Newton's method
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
is also useful for "touch up" corrections to the Gauss–Jordan algorithm
Gauss–Jordan elimination
In linear algebra, Gauss–Jordan elimination is an algorithm for getting matrices in reduced row echelon form using elementary row operations. It is a variation of Gaussian elimination. Gaussian elimination places zeros below each pivot in the matrix, starting with the top row and working downwards....
which has been contaminated by small errors due to imperfect computer arithmetic
Round-off error
A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
.
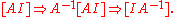
Analytic solution
Writing the transpose of the matrix of cofactors, known as an adjugate matrixAdjugate matrix
In linear algebra, the adjugate or classical adjoint of a square matrix is a matrix that plays a role similar to the inverse of a matrix; it can however be defined for any square matrix without the need to perform any divisions....
, can also be an efficient way to calculate the inverse of small matrices, but this recursive method is inefficient for large matrices. To determine the inverse, we calculate a matrix of cofactors:
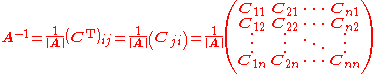
where |A| is the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of A, Cij is the matrix of cofactors, and CT represents the matrix transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
.
For most practical applications, it is not necessary to invert a matrix to solve a system of linear equations; however, for a unique solution, it is necessary that the matrix involved be invertible.
Decomposition techniques like LU decomposition
LU decomposition
In linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
are much faster than inversion, and various fast algorithms for special classes of linear systems have also been developed.
Inversion of 2×2 matrices
The cofactor equation listed above yields the following result for 2×2 matrices. Inversion of these matrices can be done easily as follows: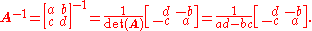This is possible because 1/(ad-bc) is the reciprocal of the determinant of the matrix in question, and the same strategy could be used for other matrix sizes.
Inversion of 3×3 matrices
A computationally efficient 3x3 matrix inversion is given by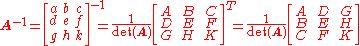where the determinant of A can be computed by applying the rule of Sarrus
Rule of Sarrus
Sarrus' rule or Sarrus' scheme is a method and a memorization scheme to compute the determinant of a 3×3 matrix. It is named after the French mathematician Pierre Frédéric Sarrus....
as follows:
If the determinant is non-zero, the matrix is invertible, with the elements of the above matrix on the right side given by
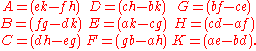
The general 3×3 inverse can be expressed concisely in terms of the cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
and triple product
Triple product
In mathematics, the triple product is a product of three vectors. The name "triple product" is used for two different products, the scalar-valued scalar triple product and, less often, the vector-valued vector triple product....
:
If a matrix
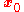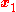(consisting of three column vectors, , , and 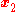) is invertible, its inverse is given by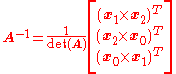where
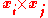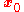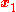is a column vector and is a row vector. Note that is equal to the triple product of , , and 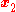—the volume of the parallelepipedParallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
formed by the rows or columns:
The correctness of the formula can be checked by using cross- and triple-product properties and by noting that for groups, left and right inverses always coincide. Intuitively, because of the cross products, each row of
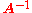is orthogonal to the non-corresponding two columns of (causing the off-diagonal terms of 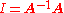be zero). Dividing by
causes the diagonal elements of
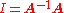to be unity. For example, the first diagonal is: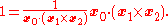Blockwise inversion
Matrices can also be inverted blockwise by using the following analytic inversion formula: |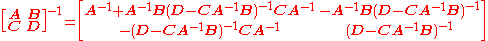
 |
where A, B, C and D are matrix sub-blocks
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
of arbitrary size. (A and D must, of course, be square, so that they can be inverted. Furthermore, this is true if and only if A and D−CA−1B are nonsingular
). This strategy is particularly advantageous if A is diagonal and D−CA−1B (the Schur complement
Schur complement
In linear algebra and the theory of matrices,the Schur complement of a matrix block is defined as follows.Suppose A, B, C, D are respectivelyp×p, p×q, q×p...
of A) is a small matrix, since they are the only matrices requiring inversion. This technique was reinvented several times and is due to Hans Boltz (1923), who used it for the inversion of geodetic matrices, and Tadeusz Banachiewicz
Tadeusz Banachiewicz
Tadeusz Banachiewicz was a Polish astronomer, mathematician and geodesist....
(1937), who generalized it and proved its correctness.
The nullity theorem
Nullity theorem
The nullity theorem is a mathematical theorem about the inverse of a partitioned matrix, which states that the nullity of a block in a matrix equals the nullity of the complementary block in its inverse matrix. Here, the nullity is the dimension of the kernel...
says that the nullity of A equals the nullity of the sub-block in the lower right of the inverse matrix, and that the nullity of B equals the nullity of the sub-block in the upper right of the inverse matrix.
The inversion procedure that led to Equation (1) performed matrix block operations that operated on C and D first. Instead, if A and B are operated on first, and provided D and A−BD−1C are nonsingular
, the result is
 |
 |
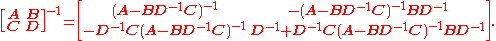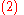Equating Equations (1) and (2) leads to
 |
 |
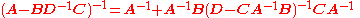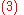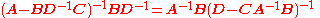
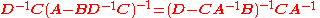
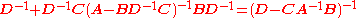
where Equation (3) is the matrix inversion lemma, which is equivalent to the binomial inverse theorem
Binomial inverse theorem
In mathematics, the Binomial Inverse Theorem is useful for expressing matrix inverses in different ways.If A, U, B, V are matrices of sizes p×p, p×q, q×q, q×p, respectively, then...
.
By Neumann series
If a matrix A has the property that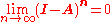then A is nonsingular and its inverse may be expressed by a Neumann series:
Truncating the sum results in an "approximate" inverse which may be useful as a preconditioner
Preconditioner
In mathematics, preconditioning is a procedure of an application of a transformation, called the preconditioner, that conditions a given problem into a form that is more suitable for numerical solution. Preconditioning is typically related to reducing a condition number of the problem...
.
More generally, if A is "near" the invertible matrix X in the sense that
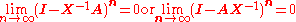
then A is nonsingular and its inverse is
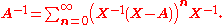
If it is also the case that A-X has rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
1 then this simplifies to
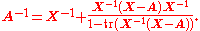
Derivative of the matrix inverse
Suppose that the invertible matrix A depends on a parameter t. Then the derivative of the inverse of A with respect to t is given by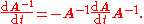To derive the above expression for the derivative of the inverse of A, one can differentiate the definition of the matrix inverse
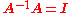and then solve for the inverse of A:
-
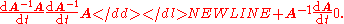
Subtracting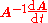
from both sides of the above and multiplying on the right by 
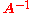gives the correct expression for the derivative of the inverse:
Similarly, if
is a small number then
-
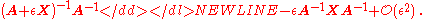
Moore–Penrose pseudoinverse
Some of the properties of inverse matrices are shared by Moore–Penrose pseudoinverses, which can be defined for any m-by-n matrix.
Matrix inverses in real-time simulations
Matrix inversion plays a significant role in computer graphicsComputer graphicsComputer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, particularly in 3D graphics rendering and 3D simulations. Examples include screen-to-world ray casting, world-to-subspace-to-world object transformations, and physical simulations.
See also
- Binomial inverse theoremBinomial inverse theoremIn mathematics, the Binomial Inverse Theorem is useful for expressing matrix inverses in different ways.If A, U, B, V are matrices of sizes p×p, p×q, q×q, q×p, respectively, then...
- LU decompositionLU decompositionIn linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
- Matrix decompositionMatrix decompositionIn the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
- PseudoinversePseudoinverseIn mathematics, and in particular linear algebra, a pseudoinverse of a matrix is a generalization of the inverse matrix. The most widely known type of matrix pseudoinverse is the Moore–Penrose pseudoinverse, which was independently described by E. H. Moore in 1920, Arne Bjerhammar in 1951 and...
- Moore–Penrose pseudoinverse
- Singular value decompositionSingular value decompositionIn linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
- Woodbury matrix identityWoodbury matrix identityIn mathematics , the Woodbury matrix identity, named after Max A. Woodbury says that the inverse of a rank-k correction of some matrix can be computed by doing a rank-k correction to the inverse of the original matrix...
External links
- Equations Solver Online
- Lecture on Inverse Matrices by Khan Academy
- Linear Algebra Lecture on Inverse Matrices by MIT
- LAPACK is a collection of FORTRAN subroutines for solving dense linear algebra problems
- ALGLIB includes a partial port of the LAPACK to C++, C#, Delphi, etc.
- Online Inverse Matrix Calculator using AJAX
- Moore Penrose Pseudoinverse
- Inverse of a Matrix Notes
- Module for the Matrix Inverse
- Calculator for Singular or Non-Square Matrix Inverse
- Binomial inverse theorem
-
