Binomial inverse theorem
Encyclopedia
In mathematics
, the Binomial Inverse Theorem is useful for expressing matrix
inverses in different ways.
If A, U, B, V are matrices of sizes p×p, p×q, q×q, q×p, respectively, then
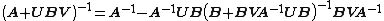
provided A and B + BVA−1UB are nonsingular. Note that if B is invertible, the two B terms flanking the quantity inverse in the right-hand side can be replaced with (B−1)−1, which results in
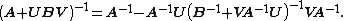
This is the matrix inversion lemma, which can also be derived using matrix blockwise inversion.
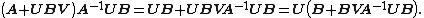
Now multiply the matrix we wish to invert by its alleged inverse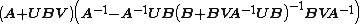
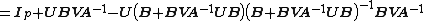
which verifies that it is the inverse.
So we get that—if A−1 and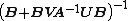
exist, then 
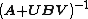exists and is given by the theorem above.
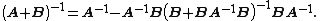
Remembering the identity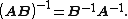
we can also express the previous equation in the simpler form as
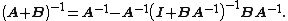
If B = Iq is the identity matrix and q = 1, then U is a column vector, written u, and V is a row vector, written vT. Then the theorem implies
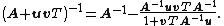
This is useful if one has a matrix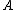
with a known inverse A−1 and one needs to invert matrices of the form A+uvT quickly.
If we set A = Ip and B = Iq, we get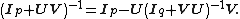
In particular, if q = 1, then
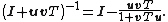
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Binomial Inverse Theorem is useful for expressing matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
inverses in different ways.
If A, U, B, V are matrices of sizes p×p, p×q, q×q, q×p, respectively, then
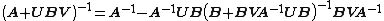
provided A and B + BVA−1UB are nonsingular. Note that if B is invertible, the two B terms flanking the quantity inverse in the right-hand side can be replaced with (B−1)−1, which results in
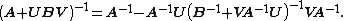
This is the matrix inversion lemma, which can also be derived using matrix blockwise inversion.
Verification
First notice that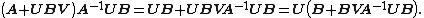Now multiply the matrix we wish to invert by its alleged inverse
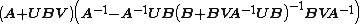
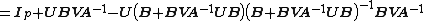
which verifies that it is the inverse.
So we get that—if A−1 and
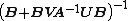exist, then 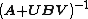exists and is given by the theorem above.Special cases
If p = q and U = V = Ip is the identity matrix, then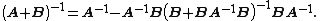Remembering the identity
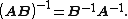
we can also express the previous equation in the simpler form as
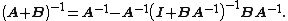
If B = Iq is the identity matrix and q = 1, then U is a column vector, written u, and V is a row vector, written vT. Then the theorem implies
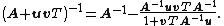
This is useful if one has a matrix
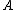with a known inverse A−1 and one needs to invert matrices of the form A+uvT quickly.If we set A = Ip and B = Iq, we get
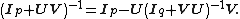
In particular, if q = 1, then
See also
- Woodbury matrix identityWoodbury matrix identityIn mathematics , the Woodbury matrix identity, named after Max A. Woodbury says that the inverse of a rank-k correction of some matrix can be computed by doing a rank-k correction to the inverse of the original matrix...
- Sherman-Morrison formulaSherman-Morrison formulaIn mathematics, in particular linear algebra, the Sherman–Morrison formula, named after Jack Sherman and Winifred J. Morrison, computes the inverse of the sum of an invertiblematrix Aand the dyadic product, u v^T,of a column vector u and a row vector v^T...
- Invertible matrix
- Matrix determinant lemmaMatrix determinant lemmaIn mathematics, in particular linear algebra, the matrix determinant lemma computes the determinant of the sum of an invertiblematrix Aand the dyadic product, u vT,of a column vector u and a row vector vT.- Statement :...
- For certain cases where A is singular and also Moore-Penrose pseudoinverse, see Kurt S. Riedel, A Sherman—Morrison—Woodbury Identity for Rank Augmenting Matrices with Application to Centering, SIAM Journal on Matrix Analysis and Applications, 13 (1992)659-662, preprint
- Moore-Penrose pseudoinverse#Updating the pseudoinverse