Gauss–Jordan elimination
Encyclopedia
In linear algebra
, Gauss–Jordan elimination is an algorithm
for getting matrices
in reduced row echelon form using elementary row operations
. It is a variation of Gaussian elimination
. Gaussian elimination places zeros below each pivot
in the matrix, starting with the top row and working downwards. Matrices containing zeros below each pivot are said to be in row echelon form. Gauss–Jordan elimination goes a step further by placing zeros above and below each pivot; such matrices are said to be in reduced row echelon form. Every matrix has a reduced row echelon form, and Gauss–Jordan elimination is guaranteed to find it.
It is named after Carl Friedrich Gauss
and Wilhelm Jordan because it is a variation of Gaussian elimination as Jordan described in 1887. However, the method also appears in an article by Clasen published in the same year. Jordan and Clasen probably discovered Gauss–Jordan elimination independently.
Computer science's complexity theory
shows Gauss–Jordan elimination to have a time complexity of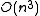
for an n by n matrix (using Big O Notation
). This result means it is efficiently solvable for most practical purposes. As a result, it is often used in computer software for a diverse set of applications. However, it is often an unnecessary step past Gaussian elimination. Gaussian elimination shares Gauss-Jordan's time complexity of
but is generally faster. Therefore, in cases in which achieving reduced row echelon form over row echelon form is unnecessary, Gaussian elimination is typically preferred.
the square matrix with the identity matrix
of the same dimensions and applying the following matrix operations: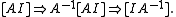
If the original square matrix,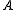
, is given by the following expression: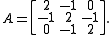
Then, after augmenting by the identity, the following is obtained:
By performing elementary row operations on the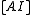
matrix until it reaches reduced row echelon form, the following is the final result:
The matrix augmentation can now be undone, which gives the following: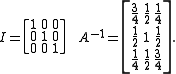
A matrix is non-singular (meaning that it has an inverse matrix) if and only if
the identity matrix can be obtained using only elementary row operations.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, Gauss–Jordan elimination is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
for getting matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
in reduced row echelon form using elementary row operations
Elementary row operations
In mathematics, an elementary matrix is a simple matrix which differs from the identity matrix by one single elementary row operation. The elementary matrices generate the general linear group of invertible matrices...
. It is a variation of Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
. Gaussian elimination places zeros below each pivot
Pivot element
The pivot or pivot element is the element of a matrix, an array, or some other kind of finite set, which is selected first by an algorithm , to do certain calculations...
in the matrix, starting with the top row and working downwards. Matrices containing zeros below each pivot are said to be in row echelon form. Gauss–Jordan elimination goes a step further by placing zeros above and below each pivot; such matrices are said to be in reduced row echelon form. Every matrix has a reduced row echelon form, and Gauss–Jordan elimination is guaranteed to find it.
It is named after Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
and Wilhelm Jordan because it is a variation of Gaussian elimination as Jordan described in 1887. However, the method also appears in an article by Clasen published in the same year. Jordan and Clasen probably discovered Gauss–Jordan elimination independently.
Computer science's complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
shows Gauss–Jordan elimination to have a time complexity of
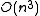for an n by n matrix (using Big O NotationBig O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
). This result means it is efficiently solvable for most practical purposes. As a result, it is often used in computer software for a diverse set of applications. However, it is often an unnecessary step past Gaussian elimination. Gaussian elimination shares Gauss-Jordan's time complexity of
but is generally faster. Therefore, in cases in which achieving reduced row echelon form over row echelon form is unnecessary, Gaussian elimination is typically preferred.Application to finding inverses
If Gauss–Jordan elimination is applied on a square matrix, it can be used to calculate the matrix's inverse. This can be done by augmentingAugmented matrix
In linear algebra, an augmented matrix is a matrix obtained by appending the columns of two given matrices, usually for the purpose of performing the same elementary row operations on each of the given matrices.Given the matrices A and B, where:A =...
the square matrix with the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
of the same dimensions and applying the following matrix operations:
If the original square matrix,
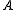, is given by the following expression: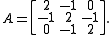Then, after augmenting by the identity, the following is obtained:
By performing elementary row operations on the
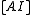matrix until it reaches reduced row echelon form, the following is the final result:The matrix augmentation can now be undone, which gives the following:
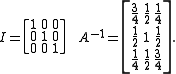
A matrix is non-singular (meaning that it has an inverse matrix) if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the identity matrix can be obtained using only elementary row operations.
External links
- Gauss-Jordan Solver Online
- Algorithm for Gauss–Jordan elimination in Octave
- Algorithm for Gauss–Jordan elimination in Python
- An online tool solve nxm linear systems using Gauss–Jordan elimination (source-code and mobile version included), by Felipe Santos de Andrade (Portuguese)
- Algorithm for Gauss–Jordan elimination in Basic
- Module for Gauss–Jordan Elimination
- Example of Gauss–Jordan Elimination "Step-by-Step"
- Gauss–Jordan Elimination Calculator
- Example of detailed solutions SLE in four unknowns using the Gauss-Jordan elimination