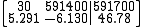Pivot element
Encyclopedia
The pivot or pivot element is the element of a matrix
, an array, or some other kind of finite set, which is selected first by an algorithm
(e.g. Gaussian elimination
, Quicksort, Simplex algorithm
, etc.), to do certain calculations. In the case of matrix algorithms, a pivot entry is usually required to be at least distinct from zero, and often distant from it; in this case finding this element is called pivoting. Pivoting may be followed by an interchange of rows or columns to bring the pivot to a fixed position and allow the algorithm to proceed successfully, and possibly to reduce round-off error.
Pivoting might be thought of as swapping or sorting rows or columns in a matrix, and thus it can be represented as multiplication
by permutation matrices
. However, algorithms rarely move the matrix elements because this would cost too much time; instead, they just keep track of the permutations.
The pivot element in quicksort is the element that is selected as the boundary for partitioning. Quicksort sorts all elements "left" and "right" of the pivot element recursively
.
Overall, pivoting adds more operations to the computational cost of an algorithm. These additional operations are sometimes necessary for the algorithm to work at all. Other times these additional operations are worthwhile because they add numerical stability
to the final result.
Interchanging rows or columns in the case of a zero pivot element is necessary. The system below requires the interchange of rows 2 and 3 to perform elimination.

The system that results from pivoting is as follows and will allow the elimination algorithm and backwards substitution to output the solution to the system.
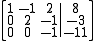
Furthermore, in Gaussian elimination it is generally desirable to choose a pivot element with large absolute value
. This improves the numerical stability
. The following system is dramatically affected by round-off error when Gaussian elimination and backwards substitution are performed.
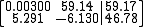
This system has the exact solution of x1 = 10.00 and x2 = 1.000, but when the elimination algorithm and backwards substitution are performed using four-digit arithmetic, the small value of a11 causes small round-off errors to be propagated. The algorithm without pivoting yields the approximation of x1 ≈ 9873.3 and x2 ≈ 4. In this case it is desirable that we interchange the two rows so that a21 is in the pivot position
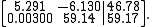
Considering this system, the elimination algorithm and backwards substitution using four-digit arithmetic yield the correct values x1 = 10.00 and x2 = 1.000.
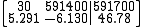
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, an array, or some other kind of finite set, which is selected first by an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
(e.g. Gaussian elimination
Gaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
, Quicksort, Simplex algorithm
Simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
, etc.), to do certain calculations. In the case of matrix algorithms, a pivot entry is usually required to be at least distinct from zero, and often distant from it; in this case finding this element is called pivoting. Pivoting may be followed by an interchange of rows or columns to bring the pivot to a fixed position and allow the algorithm to proceed successfully, and possibly to reduce round-off error.
Pivoting might be thought of as swapping or sorting rows or columns in a matrix, and thus it can be represented as multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
by permutation matrices
Permutation matrix
In mathematics, in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry 1 in each row and each column and 0s elsewhere...
. However, algorithms rarely move the matrix elements because this would cost too much time; instead, they just keep track of the permutations.
The pivot element in quicksort is the element that is selected as the boundary for partitioning. Quicksort sorts all elements "left" and "right" of the pivot element recursively
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
.
Overall, pivoting adds more operations to the computational cost of an algorithm. These additional operations are sometimes necessary for the algorithm to work at all. Other times these additional operations are worthwhile because they add numerical stability
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
to the final result.
Examples of systems that require pivoting
In the case of Gaussian elimination, the algorithm requires that pivot elements not be zero.Interchanging rows or columns in the case of a zero pivot element is necessary. The system below requires the interchange of rows 2 and 3 to perform elimination.

The system that results from pivoting is as follows and will allow the elimination algorithm and backwards substitution to output the solution to the system.
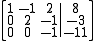
Furthermore, in Gaussian elimination it is generally desirable to choose a pivot element with large absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
. This improves the numerical stability
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
. The following system is dramatically affected by round-off error when Gaussian elimination and backwards substitution are performed.
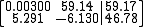
This system has the exact solution of x1 = 10.00 and x2 = 1.000, but when the elimination algorithm and backwards substitution are performed using four-digit arithmetic, the small value of a11 causes small round-off errors to be propagated. The algorithm without pivoting yields the approximation of x1 ≈ 9873.3 and x2 ≈ 4. In this case it is desirable that we interchange the two rows so that a21 is in the pivot position
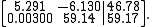
Considering this system, the elimination algorithm and backwards substitution using four-digit arithmetic yield the correct values x1 = 10.00 and x2 = 1.000.
Partial and complete pivoting
In partial pivoting, the algorithm selects the entry with largest absolute value from the column of the matrix that is currently being considered as the pivot element. Partial pivoting is generally sufficient to adequately reduce round-off error. However for certain systems and algorithms, complete pivoting (or maximal pivoting) may be required for acceptable accuracy. Complete pivoting considers all entries in the whole matrix, interchanging rows and columns to achieve the highest accuracy. Complete pivoting is usually not necessary to ensure numerical stability and, due to the additional computations it introduces, it may not always be the most appropriate pivoting strategy.Scaled pivoting
A variation of the partial pivoting strategy is scaled partial pivoting. In this approach, the algorithm selects as the pivot element the entry that is largest relative to the entries in its row. This strategy is desirable when entries' large differences in magnitude lead to the propagation of round-off error. Scaled pivoting should be used in a system like the one below where a row's entries vary greatly in magnitude. In the example below, it would be desirable to interchange the two rows because the current pivot element 30 is larger than 5.291 but it is relatively small compared with the other entries in its row. Without row interchange in this case, rounding errors will be propagated as in the previous example.