Numerical stability
Encyclopedia
In the mathematical
subfield of numerical analysis
, numerical stability is a desirable property of numerical algorithm
s. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm.
A related phenomenon is instability. Typically, algorithms would approach the right solution in the limit, if there were no round-off or truncation errors, but depending on the specific computational method, errors can be magnified, instead of damped, causing the error to grow exponentially.
Sometimes a single calculation can be achieved in several ways, all of which are algebraically equivalent in terms of ideal real or complex numbers, but in practice when performed on digital computers yield different results. Some calculations might damp out approximation errors that occur; others might magnify such errors. Calculations that can be proven not to magnify approximation errors are called numerically stable. One of the common tasks of numerical analysis is to try to select algorithms which are robust — that is to say, have good numerical stability among other desirable properties.
The naive way to do this would be the following:
That looks reasonable, but suppose the first element in the array was 1.0 and the other 99 elements were 0.01. In exact arithmetic, the answer would be 1.99. However, on our two-digit computer, once the 1.0 was added into the sum variable, adding in 0.01 would have no effect on the sum, and so the final answer would be 1.0 – not a very good approximation of the real answer. Furthermore, we see that the algorithm depends on the ordering of elements within the array, in contrast to the exact arithmetic.
A stable algorithm would first sort the array by the absolute values of the elements in ascending order. This ensures that the numbers closest to zero will be taken into consideration first. Once that change is made, all of the 0.01 elements will be added, giving 0.99, and then the 1.0 element will be added, yielding a rounded result of 2.0 – a much better approximation of the real result.
.
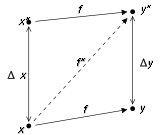Consider the problem to be solved by the numerical algorithm as a function
f mapping the data x to the solution y. The result of the algorithm, say y*, will usually deviate from the "true" solution y. The main causes of error are round-off error
and truncation error
. The forward error of the algorithm is the difference between the result and the solution; in this case, Δy = y* − y. The backward error is the smallest Δx such that f(x + Δx) = y*; in other words, the backward error tells us what problem the algorithm actually solved. The forward and backward error are related by the condition number
: the forward error is at most as big in magnitude as the condition number multiplied by the magnitude of the backward error.
In many cases, it is more natural to consider the relative error
instead of the absolute error Δx.
The algorithm is said to be backward stable if the backward error is small for all inputs x. Of course, "small" is a relative term and its definition will depend on the context. Often, we want the error to be of the same order as, or perhaps only a few orders of magnitude bigger than, the unit round-off.
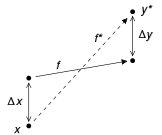The usual definition of numerical stability uses a more general concept, called mixed stability, which combines the forward error and the backward error. An algorithm is stable in this sense if it solves a nearby problem approximately, i.e., if there exists a Δx such that both Δx is small and f(x + Δx) − y* is small. Hence, a backward stable algorithm is always stable.
An algorithm is forward stable if its forward error divided by the condition number of the problem is small. This means that an algorithm is forward stable if it has a forward error of magnitude similar to some backward stable algorithm.
s, a different definition of numerical stability is used.
In numerical ordinary differential equations
, various concepts of numerical stability exist, for instance A-stability. They are related to some concept of stability in the dynamical systems sense, often Lyapunov stability
. It is important to use a stable method when solving a stiff equation
.
Yet another definition is used in numerical partial differential equations
. An algorithm for solving a linear evolutionary partial differential equation
is stable if the total variation
of the numerical solution at a fixed time remains bounded as the step size goes to zero. The Lax equivalence theorem
states that an algorithm converges if it is consistent and stable (in this sense). Stability is sometimes achieved by including numerical diffusion
. Numerical diffusion is a mathematical term which ensures that roundoff and other errors in the calculation get spread out and do not add up to cause the calculation to "blow up". von Neumann stability analysis
is a commonly used procedure for the stability analysis of finite difference schemes as applied to linear partial differential equations. These results do not hold for nonlinear PDEs, where a general, consistent definition of stability is complicated by many properties absent in linear equations.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
subfield of numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, numerical stability is a desirable property of numerical algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm.
A related phenomenon is instability. Typically, algorithms would approach the right solution in the limit, if there were no round-off or truncation errors, but depending on the specific computational method, errors can be magnified, instead of damped, causing the error to grow exponentially.
Sometimes a single calculation can be achieved in several ways, all of which are algebraically equivalent in terms of ideal real or complex numbers, but in practice when performed on digital computers yield different results. Some calculations might damp out approximation errors that occur; others might magnify such errors. Calculations that can be proven not to magnify approximation errors are called numerically stable. One of the common tasks of numerical analysis is to try to select algorithms which are robust — that is to say, have good numerical stability among other desirable properties.
Example
As an example of an unstable algorithm, consider the task of adding an array of 100 numbers. To simplify things, assume our computer only has two digits of precision (for example, numbers can be represented as 2.3, 77, 100, 110, 120, etc., but not 12.3 or 177).The naive way to do this would be the following:
function sumArray(array) is
let theSum = 0
for each element in array do
let theSum = theSum + element
end for
return theSum
end functionThat looks reasonable, but suppose the first element in the array was 1.0 and the other 99 elements were 0.01. In exact arithmetic, the answer would be 1.99. However, on our two-digit computer, once the 1.0 was added into the sum variable, adding in 0.01 would have no effect on the sum, and so the final answer would be 1.0 – not a very good approximation of the real answer. Furthermore, we see that the algorithm depends on the ordering of elements within the array, in contrast to the exact arithmetic.
A stable algorithm would first sort the array by the absolute values of the elements in ascending order. This ensures that the numbers closest to zero will be taken into consideration first. Once that change is made, all of the 0.01 elements will be added, giving 0.99, and then the 1.0 element will be added, yielding a rounded result of 2.0 – a much better approximation of the real result.
Forward, backward, and mixed stability
There are different ways to formalize the concept of stability. The following definitions of forward, backward, and mixed stability are often used in numerical linear algebraNumerical linear algebra
Numerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
.
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f mapping the data x to the solution y. The result of the algorithm, say y*, will usually deviate from the "true" solution y. The main causes of error are round-off error
Round-off error
A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
and truncation error
Truncation error
Truncation error or local truncation error is error made by numerical algorithms that arises from taking finite number of steps in computation...
. The forward error of the algorithm is the difference between the result and the solution; in this case, Δy = y* − y. The backward error is the smallest Δx such that f(x + Δx) = y*; in other words, the backward error tells us what problem the algorithm actually solved. The forward and backward error are related by the condition number
Condition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
: the forward error is at most as big in magnitude as the condition number multiplied by the magnitude of the backward error.
In many cases, it is more natural to consider the relative error
instead of the absolute error Δx.
The algorithm is said to be backward stable if the backward error is small for all inputs x. Of course, "small" is a relative term and its definition will depend on the context. Often, we want the error to be of the same order as, or perhaps only a few orders of magnitude bigger than, the unit round-off.
An algorithm is forward stable if its forward error divided by the condition number of the problem is small. This means that an algorithm is forward stable if it has a forward error of magnitude similar to some backward stable algorithm.
Error growth
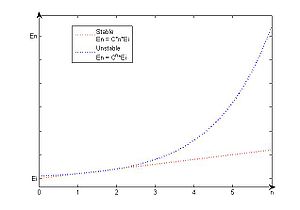
Definition
Suppose that Ei > 0 denotes an initial error and En represents the magnitude of an error after n subsequent operations. If En ≈ C*n*Ei, where C is a constant independent of n, then the growth of the error is said to be linear. If En ≈ Cn*Ei, for some C > 1, then the growth of the error is called exponential.Stability in numerical differential equations
The above definitions are particularly relevant in situations where truncation errors are not important. In other contexts, for instance when solving differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s, a different definition of numerical stability is used.
In numerical ordinary differential equations
Numerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
, various concepts of numerical stability exist, for instance A-stability. They are related to some concept of stability in the dynamical systems sense, often Lyapunov stability
Lyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
. It is important to use a stable method when solving a stiff equation
Stiff equation
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proved difficult to formulate a precise definition of stiffness, but the main idea is that...
.
Yet another definition is used in numerical partial differential equations
Numerical partial differential equations
Numerical partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations .Numerical techniques for solving PDEs include the following:...
. An algorithm for solving a linear evolutionary partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
is stable if the total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
of the numerical solution at a fixed time remains bounded as the step size goes to zero. The Lax equivalence theorem
Lax equivalence theorem
In numerical analysis, the Lax equivalence theorem is the fundamental theorem in the analysis of finite difference methods for the numerical solution of partial differential equations...
states that an algorithm converges if it is consistent and stable (in this sense). Stability is sometimes achieved by including numerical diffusion
Numerical diffusion
Numerical diffusion is a difficulty with computer simulations of continua wherein the simulated medium exhibits a higher diffusivity than the true medium...
. Numerical diffusion is a mathematical term which ensures that roundoff and other errors in the calculation get spread out and do not add up to cause the calculation to "blow up". von Neumann stability analysis
Von Neumann stability analysis
In numerical analysis, von Neumann stability analysis is a procedure used to check the stability of finite difference schemes as applied to linear partial differential equations...
is a commonly used procedure for the stability analysis of finite difference schemes as applied to linear partial differential equations. These results do not hold for nonlinear PDEs, where a general, consistent definition of stability is complicated by many properties absent in linear equations.