
Nullity theorem
Encyclopedia
The nullity theorem is a mathematical theorem
about the inverse of a partitioned matrix, which states that the nullity of a block in a matrix equals the nullity of the complementary block in its inverse matrix. Here, the nullity is the dimension of the kernel. The theorem was proven in an abstract setting by , and for matrices by .
Partition a matrix and its inverse in four submatrices: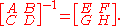
The partition on the right-hand side should be the transpose of the partition on the left-hand side, in the sense that if A is an m-by-n block then E should be an n-by-m block.
The statement of the nullity theorem is now that the nullities of the blocks on the right equal the nullities of the blocks on the left :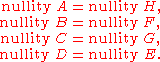
More generally, if a submatrix is formed from the rows with indices {i1, i2, …, im} and the columns with indices {j1, j2, …, jn}, then the complementary submatrix is formed from the rows with indices {1, 2, …, N} \ {j1, j2, …, jn} and the columns with indices {1, 2, …, N} \ {i1, i2, …, im}, where N is the size of the whole matrix. The nullity theorem states that the nullity of any submatrix equals the nullity of the complementary submatrix of the inverse.
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
about the inverse of a partitioned matrix, which states that the nullity of a block in a matrix equals the nullity of the complementary block in its inverse matrix. Here, the nullity is the dimension of the kernel. The theorem was proven in an abstract setting by , and for matrices by .
Partition a matrix and its inverse in four submatrices:
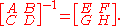
The partition on the right-hand side should be the transpose of the partition on the left-hand side, in the sense that if A is an m-by-n block then E should be an n-by-m block.
The statement of the nullity theorem is now that the nullities of the blocks on the right equal the nullities of the blocks on the left :
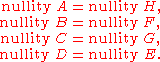
More generally, if a submatrix is formed from the rows with indices {i1, i2, …, im} and the columns with indices {j1, j2, …, jn}, then the complementary submatrix is formed from the rows with indices {1, 2, …, N} \ {j1, j2, …, jn} and the columns with indices {1, 2, …, N} \ {i1, i2, …, im}, where N is the size of the whole matrix. The nullity theorem states that the nullity of any submatrix equals the nullity of the complementary submatrix of the inverse.

