Schur complement
Encyclopedia
In linear algebra
and the theory of matrices
,
the Schur complement of a matrix block (i.e., a submatrix within a
larger matrix) is defined as follows.
Suppose A, B, C, D are respectively
p×p, p×q, q×p
and q×q matrices, and D is invertible.
Let
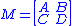
so that M is a (p+q)×(p+q) matrix.
Then the Schur complement of the block D of the
matrix M is the p×p matrix
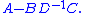
It is named after Issai Schur
who used it to prove Schur's lemma
, although it had been used previously. Emilie Haynsworth was the first to call it the Schur complement.
by multiplying the matrix M from the right with the "block lower triangular" matrix
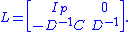
Here Ip denotes a p×p identity matrix
. After multiplication with the matrix L the Schur complement appears in the upper p×p block. The product matrix is
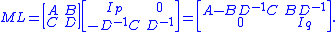
The inverse of M thus may be expressed involving D−1 and the inverse of Schur's complement (if it exists) only as
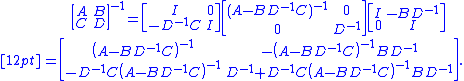
If M is a positive-definite
symmetric matrix, then so is the Schur complement of D in M.
If p and q are both 1 (i.e. A, B, C and D are all scalars), we get the familiar formula for the inverse of a 2-by-2 matrix:
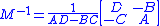
provided that AD − BC
is non-zero.
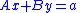
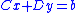
where x, a are p-dimensional column vectors, y, b are q-dimensional column vectors, and A, B, C, D are as above. Multiplying the bottom equation by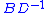
and then subtracting from the top equation one obtains
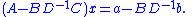
Thus if one can invert D as well as the Schur complement of D, one can solve for x, and
then by using the equation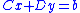
one can solve for y. This reduces the problem of
inverting a
matrix to that of inverting a p×p matrix and a q×q matrix. In practice one needs D to be well-conditioned
in order for this algorithm to be numerically accurate.
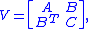
where A is n-by-n and C is m-by-m.
Then the conditional variance
of X given Y is the Schur complement of C in V:
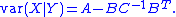
If we take the matrix V above to be, not a variance of a random vector, but a sample variance, then it may have a Wishart distribution. In that case, the Schur complement of C in V also has a Wishart distribution.
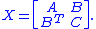
Let S be the Schur complement of A in X, that is:
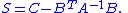
Then
These statements can be derived by considering the minimizer of the quantity
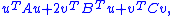
as a function of u (for fixed v).
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
and the theory of matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
,
the Schur complement of a matrix block (i.e., a submatrix within a
larger matrix) is defined as follows.
Suppose A, B, C, D are respectively
p×p, p×q, q×p
and q×q matrices, and D is invertible.
Let
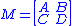
so that M is a (p+q)×(p+q) matrix.
Then the Schur complement of the block D of the
matrix M is the p×p matrix
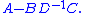
It is named after Issai Schur
Issai Schur
Issai Schur was a mathematician who worked in Germany for most of his life. He studied at Berlin...
who used it to prove Schur's lemma
Schur's lemma
In mathematics, Schur's lemma is an elementary but extremely useful statement in representation theory of groups and algebras. In the group case it says that if M and N are two finite-dimensional irreducible representations...
, although it had been used previously. Emilie Haynsworth was the first to call it the Schur complement.
Background
The Schur complement arises as the result of performing a block Gaussian eliminationGaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
by multiplying the matrix M from the right with the "block lower triangular" matrix
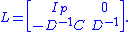
Here Ip denotes a p×p identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. After multiplication with the matrix L the Schur complement appears in the upper p×p block. The product matrix is
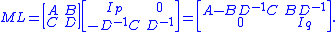
The inverse of M thus may be expressed involving D−1 and the inverse of Schur's complement (if it exists) only as
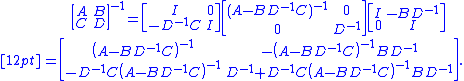
If M is a positive-definite
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
symmetric matrix, then so is the Schur complement of D in M.
If p and q are both 1 (i.e. A, B, C and D are all scalars), we get the familiar formula for the inverse of a 2-by-2 matrix:
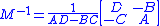
provided that AD − BC
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
is non-zero.
Application to solving linear equations
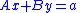
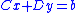
The Schur complement arises naturally in solving a system of linear equations such aswhere x, a are p-dimensional column vectors, y, b are q-dimensional column vectors, and A, B, C, D are as above. Multiplying the bottom equation by
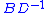and then subtracting from the top equation one obtains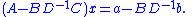Thus if one can invert D as well as the Schur complement of D, one can solve for x, and
then by using the equation
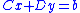one can solve for y. This reduces the problem ofinverting a
matrix to that of inverting a p×p matrix and a q×q matrix. In practice one needs D to be well-conditionedCondition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
in order for this algorithm to be numerically accurate.
Applications to probability theory and statistics
Suppose the random column vectors X, Y live in Rn and Rm respectively, and the vector (X, Y) in Rn+m has a multivariate normal distribution whose variance is the symmetric positive-definite matrix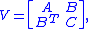where A is n-by-n and C is m-by-m.
Then the conditional variance
Conditional variance
In probability theory and statistics, a conditional variance is the variance of a conditional probability distribution. Particularly in econometrics, the conditional variance is also known as the scedastic function or skedastic function...
of X given Y is the Schur complement of C in V:
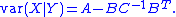
If we take the matrix V above to be, not a variance of a random vector, but a sample variance, then it may have a Wishart distribution. In that case, the Schur complement of C in V also has a Wishart distribution.
Schur complement condition for positive definiteness
Let X be a symmetric matrix given by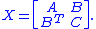Let S be the Schur complement of A in X, that is:
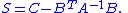
Then
- X is positive definite if and only if A and S are both positive definite
- If A is positive definite, then X is positive semidefinite if and only if S is positive semidefinite.
These statements can be derived by considering the minimizer of the quantity
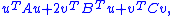
as a function of u (for fixed v).
See also
- Woodbury matrix identityWoodbury matrix identityIn mathematics , the Woodbury matrix identity, named after Max A. Woodbury says that the inverse of a rank-k correction of some matrix can be computed by doing a rank-k correction to the inverse of the original matrix...
- Quasi-Newton methodQuasi-Newton methodIn optimization, quasi-Newton methods are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on...
- Haynsworth inertia additivity formulaHaynsworth inertia additivity formulaIn mathematics, the Haynsworth inertia additivity formula, discovered by Emilie Virginia Haynsworth , concerns the number of positive, negative, and zero eigenvalues of a Hermitian matrix and of block matrices into which it is partitioned....