Conditional variance
Encyclopedia
In probability theory
and statistics
, a conditional variance is the variance
of a conditional probability distribution. Particularly in econometrics
, the conditional variance is also known as the scedastic function or skedastic function. Conditional variances are important parts of ARCH
models.
Y given that the value of a random variable X takes the value x is
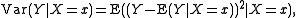
where E is the expectation operator with respect to the conditional distribution
of Y given that the X takes the value x. An alternative notation for this is :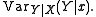
The above may be stated in the alternative form that, based on the conditional distribution
of Y given that the X takes the value x, the conditional variance is the variance
of this probability distribution
.
says
where, for example,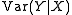
is understood to mean that the value x at which the conditional variance would is evaluated is allowed to be a random variable
, X. In this "law", the inner expectation or variance is taken with respect to Y conditional on X, while the outer expectation or variance is taken with respect to X. This expression represents the overall variance of Y as the sum of two components, involving a prediction of Y based on X. Specifically, let the predictor be the least-mean-squares prediction based on X, which is the conditional expectation
of Y given X. Then the two components are:
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a conditional variance is the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of a conditional probability distribution. Particularly in econometrics
Econometrics
Econometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...
, the conditional variance is also known as the scedastic function or skedastic function. Conditional variances are important parts of ARCH
Arch
An arch is a structure that spans a space and supports a load. Arches appeared as early as the 2nd millennium BC in Mesopotamian brick architecture and their systematic use started with the Ancient Romans who were the first to apply the technique to a wide range of structures.-Technical aspects:The...
models.
Definition
The conditional variance of a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
Y given that the value of a random variable X takes the value x is
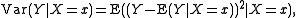
where E is the expectation operator with respect to the conditional distribution
Conditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
of Y given that the X takes the value x. An alternative notation for this is :
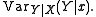
The above may be stated in the alternative form that, based on the conditional distribution
Conditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
of Y given that the X takes the value x, the conditional variance is the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of this probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
.
Components of variance
The law of total varianceLaw of total variance
In probability theory, the law of total variance or variance decomposition formula states that if X and Y are random variables on the same probability space, and the variance of Y is finite, then...
says
where, for example,
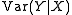is understood to mean that the value x at which the conditional variance would is evaluated is allowed to be a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, X. In this "law", the inner expectation or variance is taken with respect to Y conditional on X, while the outer expectation or variance is taken with respect to X. This expression represents the overall variance of Y as the sum of two components, involving a prediction of Y based on X. Specifically, let the predictor be the least-mean-squares prediction based on X, which is the conditional expectation
Conditional expectation
In probability theory, a conditional expectation is the expected value of a real random variable with respect to a conditional probability distribution....
of Y given X. Then the two components are:
- the average of the variance of Y about the prediction based on X, as X varies;
- the variance of the prediction based on X, as X varies.