
Conditional distribution
Encyclopedia
Given two jointly distributed random variable
s X and Y, the conditional probability distribution of Y given X is the probability distribution
of Y when X is known to be a particular value. If the conditional distribution of Y given X is a continuous distribution, then its probability density function
is known as the conditional density function.
The properties of a conditional distribution, such as the moments, are often called by corresponding names such as the conditional mean and conditional variance
.
mass function of Y given (the occurrence of) the value x of X, can be written, using the definition of conditional probability
, as:
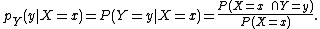
As seen from the definition, and due to its occurrence, it is necessary that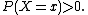
The relation with the probability distribution of X given Y is:

of Y given (the occurrence of) the value x of X, can be written as

where fX,Y(x, y) gives the joint density
of X and Y, while fX(x) gives the marginal density for X. Also in this case it is necessary that .
.
The relation with the probability distribution of X given Y is given by:
The concept of the conditional distribution of a continuous random variable is not as intuitive as it might seem: Borel's paradox
shows that conditional probability density functions need not be invariant under coordinate transformations.
of X (and this implies that X is also independent of Y).
, so that the sum over all x need not be 1.
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X and Y, the conditional probability distribution of Y given X is the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of Y when X is known to be a particular value. If the conditional distribution of Y given X is a continuous distribution, then its probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
is known as the conditional density function.
The properties of a conditional distribution, such as the moments, are often called by corresponding names such as the conditional mean and conditional variance
Conditional variance
In probability theory and statistics, a conditional variance is the variance of a conditional probability distribution. Particularly in econometrics, the conditional variance is also known as the scedastic function or skedastic function...
.
Discrete distributions
For discrete random variables, the conditional probabilityConditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
mass function of Y given (the occurrence of) the value x of X, can be written, using the definition of conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
, as:
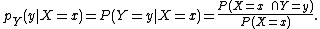
As seen from the definition, and due to its occurrence, it is necessary that
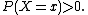
The relation with the probability distribution of X given Y is:

Continuous distributions
Similarly for continuous random variables, the conditional probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of Y given (the occurrence of) the value x of X, can be written as

where fX,Y(x, y) gives the joint density
Joint distribution
In the study of probability, given two random variables X and Y that are defined on the same probability space, the joint distribution for X and Y defines the probability of events defined in terms of both X and Y...
of X and Y, while fX(x) gives the marginal density for X. Also in this case it is necessary that
 .
.The relation with the probability distribution of X given Y is given by:

The concept of the conditional distribution of a continuous random variable is not as intuitive as it might seem: Borel's paradox
Borel's paradox
In probability theory, the Borel–Kolmogorov paradox is a paradox relating to conditional probability with respect to an event of probability zero...
shows that conditional probability density functions need not be invariant under coordinate transformations.
Relation to independence
If for discrete random variables P(Y = y | X = x) = P(Y = y) for all x and y, or for continuous random variables fY(y | X=x) = fY(y) for all x and y, then Y is said to be independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
of X (and this implies that X is also independent of Y).
Properties
Seen as a function of y for given x, P(Y = y | X = x) is a probability and so the sum over all y (or integral if it is a conditional probability density) is 1. Seen as a function of x for given y, it is a likelihood functionLikelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
, so that the sum over all x need not be 1.
See also
- Conditioning (probability)Conditioning (probability)Beliefs depend on the available information. This idea is formalized in probability theory by conditioning. Conditional probabilities, conditional expectations and conditional distributions are treated on three levels: discrete probabilities, probability density functions, and measure theory...
- Conditional probabilityConditional probabilityIn probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
- Regular conditional probabilityRegular conditional probabilityRegular conditional probability is a concept that has developed to overcome certain difficulties in formally defining conditional probabilities for continuous probability distributions...

