Joint distribution
Encyclopedia
In the study of probability
, given two random variable
s X and Y that are defined on the same probability space
, the joint distribution for X and Y defines the probability of events defined in terms of both X and Y. In the case of only two random variables, this is called a bivariate distribution, but the concept generalizes to any number of random variables, giving a multivariate distribution.
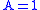if the number is even (i.e. 2,4, or 6) and 
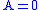otherwise. Furthermore, let 
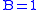if the number is prime
(i.e. 2,3, or 5) and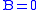
otherwise. Then, the joint distribution of 
and 
is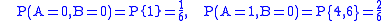
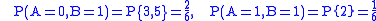
for a pair of random variables is defined in terms of their joint probability distribution;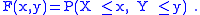
of two discrete random variables is equal to
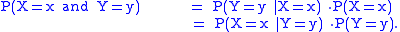
In general, the joint probability distribution of
discrete random variables 
is equal to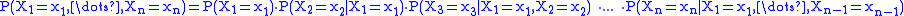
This identity is known as the chain rule of probability
.
Since these are probabilities, we have
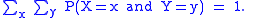
can be written as fX,Y(x, y) and this is
where fY|X(y|x) and fX|Y(x|y) give the conditional distribution
s of Y given X = x and of X given Y = y respectively, and fX(x) and fY(y) give the marginal distribution
s for X and Y respectively.
Again, since these are probability distributions, one has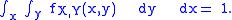
, one may wish to predict the probability of a binary outcome Y conditional on the value of a continuously-distributed X. In this case, (X, Y) has neither a probability density function nor a probability mass function in the sense of the terms given above. On the other hand, a "mixed joint density" can be defined in either of two ways:
Formally, fX,Y(x, y) is the probability density function of (X, Y) with respect to the product measure
on the respective support
s of X and Y. Either of these two decompositions can then be used to recover the joint cumulative distribution function:
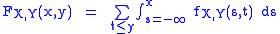
The definition generalizes to a mixture of arbitrary numbers of discrete and continuous random variables.
for a vector of random variables is defined in terms of their joint probability distribution;
The joint distribution for two random variables can be extended to many random variables X1, ... Xn by adding them sequentially with the identity
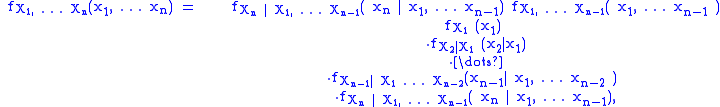
where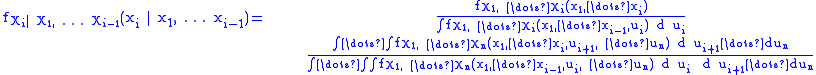
and
(notice, that these latter identities can be useful to generate a random variable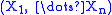
with given distribution function 
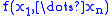); the density of the marginal distribution
is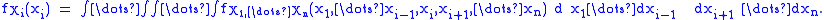
The joint cumulative distribution function is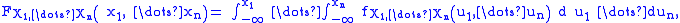
and the conditional distribution function is accordingly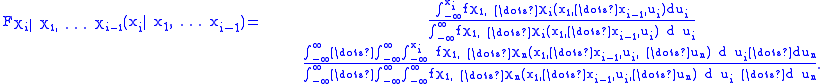
Expectation reads
suppose that h is smooth enough and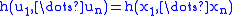
for 
, then, by iterated integration by parts
,
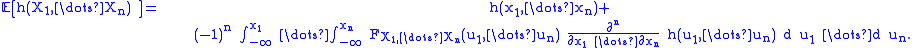
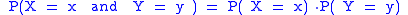for all x and y, or for absolutely continuous random variables 
for all x and y, then X and Y are said to be independent
.
of the variables 
is conditionally independent
given another subset
of these variables, then the joint distribution 
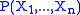is equal to 
. Therefore, it can be efficiently represented by the lower-dimensional probability distributions 
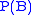and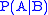 
. Such conditional independence relations can be represented with a Bayesian network
.
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
, given two random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X and Y that are defined on the same probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, the joint distribution for X and Y defines the probability of events defined in terms of both X and Y. In the case of only two random variables, this is called a bivariate distribution, but the concept generalizes to any number of random variables, giving a multivariate distribution.
Example
Consider the roll of a and let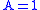 if the number is even (i.e. 2,4, or 6) and 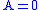otherwise. Furthermore, let 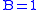if the number is primePrime
A prime is a natural number that has exactly two distinct natural number divisors: 1 and itself.Prime or PRIME may also refer to:In mathematics:*Prime , the ′ mark, typically used as a suffix...
(i.e. 2,3, or 5) and
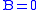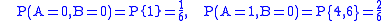
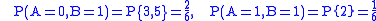
otherwise. Then, the joint distribution of and isCumulative distribution
The cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
for a pair of random variables is defined in terms of their joint probability distribution;
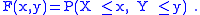
Discrete case
The joint probability mass functionProbability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
of two discrete random variables is equal to
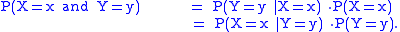
In general, the joint probability distribution of
discrete random variables is equal to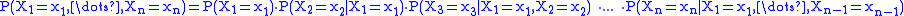This identity is known as the chain rule of probability
Chain rule (probability)
In probability theory, the chain rule permits the calculation of any member of the joint distribution of a set of random variables using only conditional probabilities.Consider an indexed set of sets A_1, \ldots A_n...
.
Since these are probabilities, we have
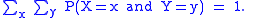
Continuous case
Similarly for continuous random variables, the joint probability density functionProbability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
can be written as fX,Y(x, y) and this is
where fY|X(y|x) and fX|Y(x|y) give the conditional distribution
Conditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
s of Y given X = x and of X given Y = y respectively, and fX(x) and fY(y) give the marginal distribution
Marginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
s for X and Y respectively.
Again, since these are probability distributions, one has
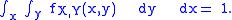
Mixed case
In some situations X is continuous but Y is discrete. For example, in a logistic regressionLogistic regression
In statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
, one may wish to predict the probability of a binary outcome Y conditional on the value of a continuously-distributed X. In this case, (X, Y) has neither a probability density function nor a probability mass function in the sense of the terms given above. On the other hand, a "mixed joint density" can be defined in either of two ways:
Formally, fX,Y(x, y) is the probability density function of (X, Y) with respect to the product measure
Product measure
In mathematics, given two measurable spaces and measures on them, one can obtain the product measurable space and the product measure on that space...
on the respective support
Support (measure theory)
In mathematics, the support of a measure μ on a measurable topological space is a precise notion of where in the space X the measure "lives"...
s of X and Y. Either of these two decompositions can then be used to recover the joint cumulative distribution function:
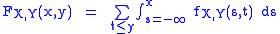
The definition generalizes to a mixture of arbitrary numbers of discrete and continuous random variables.
General multidimensional distributions
The cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
for a vector of random variables is defined in terms of their joint probability distribution;
The joint distribution for two random variables can be extended to many random variables X1, ... Xn by adding them sequentially with the identity
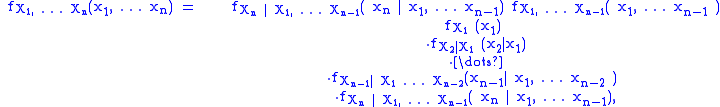
where
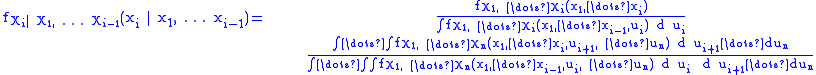
and
(notice, that these latter identities can be useful to generate a random variable
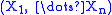with given distribution function 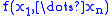); the density of the marginal distributionMarginal distribution
In probability theory and statistics, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained...
is
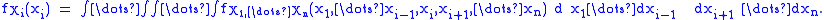
The joint cumulative distribution function is
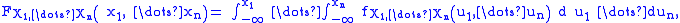
and the conditional distribution function is accordingly
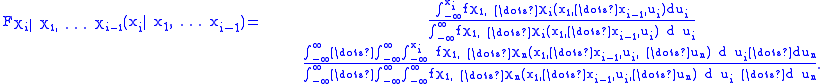
Expectation reads
suppose that h is smooth enough and
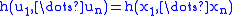for , then, by iterated integration by partsIntegration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
,
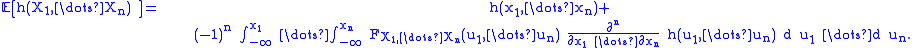
Joint distribution for independent variables
If for discrete random variables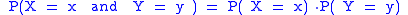 for all x and y, or for absolutely continuous random variables for all x and y, then X and Y are said to be independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
.
Joint Distribution for conditionally independent variables
If a subset of the variables is conditionally independentConditional independence
In probability theory, two events R and B are conditionally independent given a third event Y precisely if the occurrence or non-occurrence of R and the occurrence or non-occurrence of B are independent events in their conditional probability distribution given Y...
given another subset
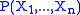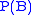of these variables, then the joint distribution is equal to . Therefore, it can be efficiently represented by the lower-dimensional probability distributions and 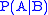. Such conditional independence relations can be represented with a Bayesian networkBayesian network
A Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph . For example, a Bayesian network could represent the probabilistic...
.
See also
- Chow-Liu treeChow-Liu treeA Chow-Liu tree is an efficient method for constructing a second-order product approximation of a joint distribution, first described in a paper by...
- Conditional probabilityConditional probabilityIn probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
- Copula (statistics)Copula (statistics)In probability theory and statistics, a copula can be used to describe the dependence between random variables. Copulas derive their name from linguistics....
- Disintegration theoremDisintegration theoremIn mathematics, the disintegration theorem is a result in measure theory and probability theory. It rigorously defines the idea of a non-trivial "restriction" of a measure to a measure zero subset of the measure space in question. It is related to the existence of conditional probability measures...
- Multivariate statisticsMultivariate statisticsMultivariate statistics is a form of statistics encompassing the simultaneous observation and analysis of more than one statistical variable. The application of multivariate statistics is multivariate analysis...
- Multivariate normal distribution
- Multivariate stable distribution
- Negative multinomial distribution
- Statistical interferenceStatistical interferenceWhen two probability distributions overlap, statistical interference exists. Knowledge of the distributions can be used to determine the likelihood that one parameter exceeds another, and by how much....