Product measure
Encyclopedia
In mathematics
, given two measurable spaces and measures
on them, one can obtain the product measurable space and the product measure on that space. Conceptually, this is similar to defining the Cartesian product
of sets and the product topology
of two topological spaces.
Let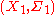
and 
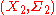be two measurable spaces, that is, 
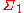and 
are sigma algebras on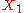 
and 
respectively, and let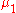 
and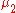 
be measures on these spaces. Denote by 
the sigma algebra on the Cartesian product
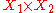generated by subset
s of the form
, where 
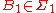and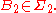 
The product measure
is defined to be the unique measure on the measurable space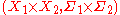 
satisfying the property
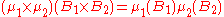
for all
In fact, when the spaces are
-finite, for every measurable set E,
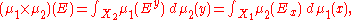
where Ex = {y∈X2|(x,y)∈E}, and Ey = {x∈X1|(x,y)∈E}, which are both measurable sets.
The existence of this measure is guaranteed by the Hahn–Kolmogorov theorem. The uniqueness of product measure is guaranteed only in case that both (X1,Σ1,μ1) and (X2,Σ2,μ2) are σ-finite.
The Borel measure on the Euclidean space
Rn can be obtained as the product of n copies of the Borel measure on the real line
R.
Even if the two factors of the product space are complete measure spaces
, the product space may not be. Consequently, the completion procedure is needed to extend the Borel measure into the Lebesgue measure
, or to extend the product of two Lebesgue measures to give the Lebesgue measure on the product space.
The opposite construction to the formation of the product of two measures is disintegration
, which in some sense "splits" a given measure into a family of measures that can be integrated to give the original measure.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, given two measurable spaces and measures
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on them, one can obtain the product measurable space and the product measure on that space. Conceptually, this is similar to defining the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of sets and the product topology
Product topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
of two topological spaces.
Let
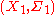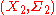and be two measurable spaces, that is, 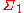and are sigma algebras on 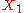and respectively, and let 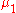and 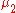be measures on these spaces. Denote by the sigma algebra on the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
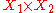generated by subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of the form
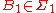, where and 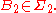The product measure
is defined to be the unique measure on the measurable space 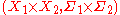satisfying the property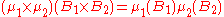 for all
In fact, when the spaces are
-finite, for every measurable set E,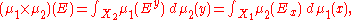where Ex = {y∈X2|(x,y)∈E}, and Ey = {x∈X1|(x,y)∈E}, which are both measurable sets.
The existence of this measure is guaranteed by the Hahn–Kolmogorov theorem. The uniqueness of product measure is guaranteed only in case that both (X1,Σ1,μ1) and (X2,Σ2,μ2) are σ-finite.
The Borel measure on the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn can be obtained as the product of n copies of the Borel measure on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R.
Even if the two factors of the product space are complete measure spaces
Complete measure
In mathematics, a complete measure is a measure space in which every subset of every null set is measurable...
, the product space may not be. Consequently, the completion procedure is needed to extend the Borel measure into the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
, or to extend the product of two Lebesgue measures to give the Lebesgue measure on the product space.
The opposite construction to the formation of the product of two measures is disintegration
Disintegration theorem
In mathematics, the disintegration theorem is a result in measure theory and probability theory. It rigorously defines the idea of a non-trivial "restriction" of a measure to a measure zero subset of the measure space in question. It is related to the existence of conditional probability measures...
, which in some sense "splits" a given measure into a family of measures that can be integrated to give the original measure.