
Marginal distribution
Encyclopedia
In probability theory
and statistics
, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained. These terms are dubbed "marginal" because they used to be found by summing values in a table along rows or columns, and writing the sum in the margins of the table. The distribution of the marginal variables (the marginal distribution) is obtained by marginalizing over the distribution of the variables being discarded, and the discarded variables are said to have been marginalized out.
The context here is that the theoretical studies being undertaken, or the data analysis
being done, involves a wider set of random variables but that attention is being limited to a reduced number of those variables. In many applications an analysis may start with a given collection of random variables, then first extend the set by defining new ones (such as the sum of the original random variables) and finally reduce the number by placing interest in the marginal distribution of a subset (such as the sum). Several different analyses may be done, each treating a different subset of variables as the marginal variables.
s X and Y whose joint distribution
is known, the marginal distribution of X is simply the probability distribution
of X averaging over information about Y. This is typically calculated by summing or integrating the joint probability distribution over Y.
For discrete random variables, the marginal probability mass function
can be written as Pr(X = x). This is
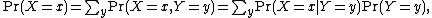
where Pr(X = x,Y = y) is the joint distribution
of X and Y, while Pr(X = x|Y = y) is the conditional distribution
of X given Y. In this case, the variable Y has been marginalized out.
Bivariate marginal and joint probabilities for discrete random variables are often displayed as two-way tables.
Similarly for continuous random variables, the marginal probability density function
can be written as pX(x). This is

where pX,Y(x,y) gives the joint distribution of X and Y, while pX|Y(x|y) gives the conditional distribution for X given Y. Again, the variable Y has been marginalized out.
Realistically, H will be dependent on L. That is, P(H = hit) and P(H = not hit) will take different values depending on whether L is red, yellow or green. You are, for example, far more likely to be hit by a car if you try to cross while the lights for cross traffic are green than if they are red. In other words, for any given possible pair of values for H and L, you must feed them into the joint probability distribution of H and L to find the probability of that pair of events occurring together.
However, in trying to calculate the marginal probability P(H=hit), what we are asking for is the probability that H=hit, where we don't actually know the particular value of L. In general you can be hit if the lights are red OR if the lights are yellow OR if the lights are green. So in this case the answer for the marginal probability can be found by summing P(H,L) = P(hit,L) for all possible values of L.
Here is a table showing the conditional probabilities of being hit, depending on the state of the lights. (Note that due to the dependence, only the columns in this table must add up to 1).
To find the joint probability distribution, we need more data. Let's say that P(L=red) = 0.7, P(L=yellow) = 0.1, P(L=green) = 0.2. Multiplying the columns in the conditional distribution by the appropriate values, we find the joint probability distribution of H and L. (Note that the cells in this table, excluding the marginal probabilities, now add up to 1).
The marginal probability P(H=Hit) is the sum of the bottom row (above the totals row), as this is the probability of being hit when the lights are red OR yellow OR green. Similarly, the marginal probability that P(H=Not Hit) is the sum of the top row. It is important to interpret this result correctly. The chance of being hit by a car when you cross the road is obviously a lot less than 17.7%. However, what this figure is actually saying is that if you were to ignore the state of the traffic lights and cross the road no matter their color, you would have a 17.7% risk of being hit by a car. This seems more reasonable.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the marginal distribution of a subset of a collection of random variables is the probability distribution of the variables contained in the subset. The term marginal variable is used to refer to those variables in the subset of variables being retained. These terms are dubbed "marginal" because they used to be found by summing values in a table along rows or columns, and writing the sum in the margins of the table. The distribution of the marginal variables (the marginal distribution) is obtained by marginalizing over the distribution of the variables being discarded, and the discarded variables are said to have been marginalized out.
The context here is that the theoretical studies being undertaken, or the data analysis
Data analysis
Analysis of data is a process of inspecting, cleaning, transforming, and modeling data with the goal of highlighting useful information, suggesting conclusions, and supporting decision making...
being done, involves a wider set of random variables but that attention is being limited to a reduced number of those variables. In many applications an analysis may start with a given collection of random variables, then first extend the set by defining new ones (such as the sum of the original random variables) and finally reduce the number by placing interest in the marginal distribution of a subset (such as the sum). Several different analyses may be done, each treating a different subset of variables as the marginal variables.
Two-variable case
Given two random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X and Y whose joint distribution
Joint distribution
In the study of probability, given two random variables X and Y that are defined on the same probability space, the joint distribution for X and Y defines the probability of events defined in terms of both X and Y...
is known, the marginal distribution of X is simply the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of X averaging over information about Y. This is typically calculated by summing or integrating the joint probability distribution over Y.
For discrete random variables, the marginal probability mass function
Probability mass function
In probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
can be written as Pr(X = x). This is
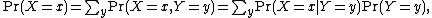
where Pr(X = x,Y = y) is the joint distribution
Joint distribution
In the study of probability, given two random variables X and Y that are defined on the same probability space, the joint distribution for X and Y defines the probability of events defined in terms of both X and Y...
of X and Y, while Pr(X = x|Y = y) is the conditional distribution
Conditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
of X given Y. In this case, the variable Y has been marginalized out.
Bivariate marginal and joint probabilities for discrete random variables are often displayed as two-way tables.
Similarly for continuous random variables, the marginal probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
can be written as pX(x). This is

where pX,Y(x,y) gives the joint distribution of X and Y, while pX|Y(x|y) gives the conditional distribution for X given Y. Again, the variable Y has been marginalized out.
Real-world example
Imagine for example you want to compute the probability that a pedestrian will be hit by a car while crossing the road at a pedestrian crossing. Let H be a discrete random variable describing the probability of being hit by a car while walking over the crossing, taking one value from { hit, not hit }. Let L be a discrete random variable describing the probability of the cross traffic's traffic light state at a given moment, taking one from { red, yellow, green }.Realistically, H will be dependent on L. That is, P(H = hit) and P(H = not hit) will take different values depending on whether L is red, yellow or green. You are, for example, far more likely to be hit by a car if you try to cross while the lights for cross traffic are green than if they are red. In other words, for any given possible pair of values for H and L, you must feed them into the joint probability distribution of H and L to find the probability of that pair of events occurring together.
However, in trying to calculate the marginal probability P(H=hit), what we are asking for is the probability that H=hit, where we don't actually know the particular value of L. In general you can be hit if the lights are red OR if the lights are yellow OR if the lights are green. So in this case the answer for the marginal probability can be found by summing P(H,L) = P(hit,L) for all possible values of L.
Here is a table showing the conditional probabilities of being hit, depending on the state of the lights. (Note that due to the dependence, only the columns in this table must add up to 1).
| Conditional distribution: P(H|L) | |||
|---|---|---|---|
| L=Red | L=Yellow | L=Green | |
| H=Not Hit | 0.99 | 0.9 | 0.2 |
| H=Hit | 0.01 | 0.1 | 0.8 |
To find the joint probability distribution, we need more data. Let's say that P(L=red) = 0.7, P(L=yellow) = 0.1, P(L=green) = 0.2. Multiplying the columns in the conditional distribution by the appropriate values, we find the joint probability distribution of H and L. (Note that the cells in this table, excluding the marginal probabilities, now add up to 1).
| Joint distribution: P(H,L) | ||||
|---|---|---|---|---|
| L=Red | L=Yellow | L=Green | Marginal probability | |
| H=Not Hit | 0.693 | 0.09 | 0.04 | 0.823 |
| H=Hit | 0.007 | 0.01 | 0.16 | 0.177 |
| Total | 0.7 | 0.1 | 0.2 | 1 |
The marginal probability P(H=Hit) is the sum of the bottom row (above the totals row), as this is the probability of being hit when the lights are red OR yellow OR green. Similarly, the marginal probability that P(H=Not Hit) is the sum of the top row. It is important to interpret this result correctly. The chance of being hit by a car when you cross the road is obviously a lot less than 17.7%. However, what this figure is actually saying is that if you were to ignore the state of the traffic lights and cross the road no matter their color, you would have a 17.7% risk of being hit by a car. This seems more reasonable.

