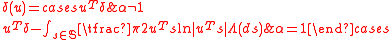Multivariate stable distribution
Encyclopedia
The multivariate stable distribution is a multivariate probability distribution
that is a multivariate generalisation of the univariate stable distribution. The multivariate stable distribution defines linear relations between stable distribution marginals. In the same way as for the univariate case, the distribution is defined in terms of its characteristic function
.
The multivariate stable distribution can also be thought as an extension of the multivariate normal distribution. It has parameter, α, which is defined over the range 0 < α ≤ 2, and where the case α = 2 is equivalent to the multivariate normal distribution. It has an additional skew parameter that allows for non-symmetric distributions, where the multivariate normal distribution is symmetric.
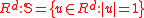 . For a random variable
. For a random variable
, X, it has a multivariate stable distribution and the notation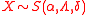 is used, if the joint characteristic function of
is used, if the joint characteristic function of  is
is
where 0 < α < 2, and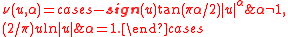
This is essentially the result of Feldheim, that any stable random vector can be characterized by a spectral measure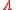 (a finite measure on
(a finite measure on 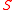 ) and a shift vector
) and a shift vector 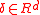 .
.
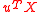 is univariate
is univariate  stable with some skewness
stable with some skewness 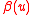 , scale
, scale 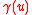 and some shift
and some shift 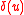 . The notation
. The notation  is used if
is used if  is stable with
is stable with
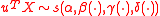
for every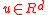 . This is called the projection parameterization.
. This is called the projection parameterization.
The spectral measure determines the projection parameter functions by:
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
that is a multivariate generalisation of the univariate stable distribution. The multivariate stable distribution defines linear relations between stable distribution marginals. In the same way as for the univariate case, the distribution is defined in terms of its characteristic function
Characteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
.
The multivariate stable distribution can also be thought as an extension of the multivariate normal distribution. It has parameter, α, which is defined over the range 0 < α ≤ 2, and where the case α = 2 is equivalent to the multivariate normal distribution. It has an additional skew parameter that allows for non-symmetric distributions, where the multivariate normal distribution is symmetric.
Definition
Let S be the unit sphere in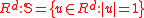 . For a random variable
. For a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, X, it has a multivariate stable distribution and the notation
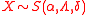 is used, if the joint characteristic function of
is used, if the joint characteristic function of  is
iswhere 0 < α < 2, and
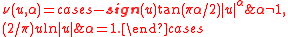
This is essentially the result of Feldheim, that any stable random vector can be characterized by a spectral measure
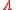 (a finite measure on
(a finite measure on 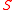 ) and a shift vector
) and a shift vector 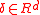 .
.Parametrization using projections
Another way to describe a stable random vector is in terms of projections. For any vector u, the projection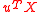 is univariate
is univariate  stable with some skewness
stable with some skewness 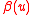 , scale
, scale 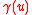 and some shift
and some shift 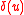 . The notation
. The notation  is used if
is used if  is stable with
is stable with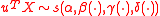
for every
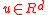 . This is called the projection parameterization.
. This is called the projection parameterization.The spectral measure determines the projection parameter functions by:
-

-
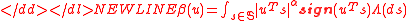
Special cases
There are four special cases where the multivariate characteristic functionCharacteristic functionIn mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
takes a simpler form. Define the characteristic function of a stable marginal as
-

Isotropic multivariate stable distribution
The characteristic function is

The spectral measure is continuous and uniform, leading to radial/isotropic symmetry.
Elliptically contoured multivariate stable distribution
Elliptically contoured m.v. stable distribution is a special symmetric case of the multivariate stable distribution.
If X is -stable and elliptically contoured, then it has joint characteristic functionCharacteristic functionIn mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
-stable and elliptically contoured, then it has joint characteristic functionCharacteristic functionIn mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...

for some positive definite matrix and shift vector
and shift vector 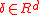 .
.
Note the relation to characteristic function of the multivariate normal distribution: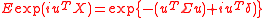 .
.
In other words, when α = 2 we get the characteristic function of the multivariate normal distribution.
Independent components
The marginals are independent with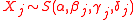 , then the
, then the
characteristic function is-

Heatmap showing a multivariate (bivariate) independent stable distribution with α = 1
Heatmap showing a multivariate (bivariate) independent stable distribution with α = 2.
Discrete
If the spectral measure is discrete with mass at
at 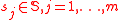
the characteristic function is
Linear properties
if is d-dim, and A is a m x d matrix,
is d-dim, and A is a m x d matrix, 
then AX + b is m dim. -stable with scale function
-stable with scale function 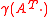
, skewness function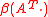 ,
,
and location function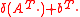
Inference in the independent component model
Recently it was shown how to compute inference in closed-form in a linear model (or equivalently a factor analysisFactor analysisFactor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved, uncorrelated variables called factors. In other words, it is possible, for example, that variations in three or four observed variables...
model),involving independent component models.
More specifically, let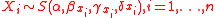 be a set of i.i.d. unobserved univariate drawn from a stable distribution. Given a known linear relation matrix A of size
be a set of i.i.d. unobserved univariate drawn from a stable distribution. Given a known linear relation matrix A of size  , the observation
, the observation  are assumed to be distributed as a convolution of the hidden factors
are assumed to be distributed as a convolution of the hidden factors  .
. 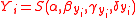 . The inference task is to compute the most probable
. The inference task is to compute the most probable  , given the linear relation matrix A and the observations
, given the linear relation matrix A and the observations 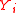 . This task can be computed in closed-form in O(n3).
. This task can be computed in closed-form in O(n3).
An application for this construction is multiuser detectionMultiuser detectionMultiuser detection is one of the receiver design technology for detecting desired signal from interference and noise. Traditionally single-user receiver is known suffering from the so-called near-far problem, where a near-by or strong signal source may block the signal receiption of far-away or...
with stable, non-Gaussian noise.
Resources
- Mark Veillette's stable distribution matlab package http://math.bu.edu/people/mveillet/research.html
- The plots in this page where plotted using Danny Bickson's inference in linear-stable model Matlab package: http://www.cs.cmu.edu/~bickson/stable
-
-
-
-