Wishart distribution
Encyclopedia
In statistics
, the Wishart distribution is a generalization to multiple dimensions of the chi-squared distribution, or, in the case of non-integer degrees of freedom, of the gamma distribution. It is named in honor of John Wishart
, who first formulated the distribution in 1928.
It is any of a family of probability distribution
s defined over symmetric, nonnegative-definite matrix-valued random variable
s (“random matrices”). These distributions are of great importance in the estimation of covariance matrices
in multivariate statistics
. In Bayesian inference
, the Wishart distribution is of particular importance, as it is the conjugate prior
of the inverse of the covariance matrix
(the precision matrix) of a multivariate normal distribution.
drawn from a p-variate normal distribution with zero mean:
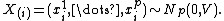
Then the Wishart distribution is the probability distribution
of the p×p random matrix
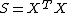
known as the scatter matrix
. One indicates that S has that probability distribution
by writing
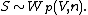
The positive integer n is the number of degrees of freedom
. Sometimes this is written W(V, p, n).
For n ≥ p the matrix S is invertible with probability 1 if V is invertible.
If p = 1 and V = 1 then this distribution is a chi-squared distribution with n degrees of freedom.
s in multivariate statistical analysis. It also arises in the spectral theory of random matrices
and in multidimensional Bayesian analysis.
by its probability density function
, as follows.
Let W be a p × p symmetric matrix of random variables that is positive definite. Let V be a (fixed) positive definite matrix of size p × p.
Then, if n ≥ p, W has a Wishart distribution with n degrees of freedom if it has a probability density function
given by
where Γp(·) is the multivariate gamma function
defined as
In fact the above definition can be extended to any real n > p − 1. If n ≤ p − 2, then the Wishart no longer has a density—instead it represents a singular distribution.
of the Wishart distribution is
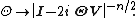
In other words,
where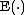
denotes expectation. (Here 
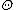and 
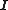are matrices the same size as 
(
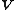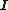is the identity matrix
); and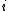
is the square root of −1).
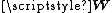has a Wishart distribution with m degrees of freedom and variance matrix 
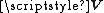—write 
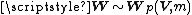—and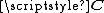 
is a q × p matrix of rank q, then
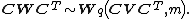
is a nonzero 
constant vector, then
.
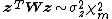In this case,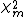
is
the chi-squared distribution and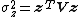
(note that 
is a constant; it is positive because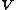 
is positive definite).
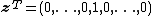(that is, the jth element is one and all others zero). Then corollary 1 above shows that
gives the marginal distribution of each of the elements on the matrix's diagonal.
Noted statistician George Seber points out that the Wishart distribution is not called the “multivariate chi-squared distribution” because the marginal distribution of the off-diagonal elements is not chi-squared. Seber prefers to reserve the term multivariate
for the case when all univariate marginals belong to the same family.
of the maximum-likelihood estimator
(MLE) of the covariance matrix
of a multivariate normal distribution with zero means. The derivation of the MLE is perhaps surprisingly subtle and elegant. It involves the spectral theorem
and the reason why it can be better to view a scalar
as the trace of a 1×1 matrix than as a mere scalar. See estimation of covariance matrices
.
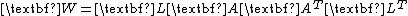
where L is the Cholesky decomposition
of V, and:
where
and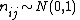 
independently.
This provides a useful method for obtaining random samples from a Wishart distribution.
This set is named after Gindikin, who introduced it in the seventies
in the context of gamma distributions on homogeneous cones. However, for the new parameters in the discrete spectrum of the Gindikin ensemble, namely,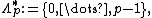
the corresponding Wishart distribution has no Lebesgue density.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Wishart distribution is a generalization to multiple dimensions of the chi-squared distribution, or, in the case of non-integer degrees of freedom, of the gamma distribution. It is named in honor of John Wishart
John Wishart (statistician)
John Wishart was a Scottish mathematician and agricultural statistician.He worked successively at University College London with Karl Pearson, at Rothamsted Experimental Station with Ronald Fisher, and then as a reader in statistics in the University of Cambridge where he became the first...
, who first formulated the distribution in 1928.
It is any of a family of probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s defined over symmetric, nonnegative-definite matrix-valued random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s (“random matrices”). These distributions are of great importance in the estimation of covariance matrices
Estimation of covariance matrices
In statistics, sometimes the covariance matrix of a multivariate random variable is not known but has to be estimated. Estimation of covariance matrices then deals with the question of how to approximate the actual covariance matrix on the basis of a sample from the multivariate distribution...
in multivariate statistics
Multivariate statistics
Multivariate statistics is a form of statistics encompassing the simultaneous observation and analysis of more than one statistical variable. The application of multivariate statistics is multivariate analysis...
. In Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
, the Wishart distribution is of particular importance, as it is the conjugate prior
Conjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
of the inverse of the covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
(the precision matrix) of a multivariate normal distribution.
Definition
Suppose X is an n × p matrix, each row of which is independentlyStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
drawn from a p-variate normal distribution with zero mean:
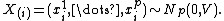
Then the Wishart distribution is the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the p×p random matrix
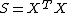
known as the scatter matrix
Scatter matrix
In multivariate statistics and probability theory, the scatter matrix is a statistic that is used to make estimates of the covariance matrix of the multivariate normal distribution.-Definition:...
. One indicates that S has that probability distribution
by writing
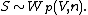
The positive integer n is the number of degrees of freedom
Degrees of freedom (statistics)
In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
. Sometimes this is written W(V, p, n).
For n ≥ p the matrix S is invertible with probability 1 if V is invertible.
If p = 1 and V = 1 then this distribution is a chi-squared distribution with n degrees of freedom.
Occurrence
The Wishart distribution arises as the distribution of the sample covariance matrix for a sample from a multivariate normal distribution. It occurs frequently in likelihood-ratio testLikelihood-ratio test
In statistics, a likelihood ratio test is a statistical test used to compare the fit of two models, one of which is a special case of the other . The test is based on the likelihood ratio, which expresses how many times more likely the data are under one model than the other...
s in multivariate statistical analysis. It also arises in the spectral theory of random matrices
Random matrix
In probability theory and mathematical physics, a random matrix is a matrix-valued random variable. Many important properties of physical systems can be represented mathematically as matrix problems...
and in multidimensional Bayesian analysis.
Probability density function
The Wishart distribution can be characterizedCharacterization (mathematics)
In mathematics, the statement that "Property P characterizes object X" means, not simply that X has property P, but that X is the only thing that has property P. It is also common to find statements such as "Property Q characterises Y up to isomorphism". The first type of statement says in...
by its probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
, as follows.
Let W be a p × p symmetric matrix of random variables that is positive definite. Let V be a (fixed) positive definite matrix of size p × p.
Then, if n ≥ p, W has a Wishart distribution with n degrees of freedom if it has a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
given by
where Γp(·) is the multivariate gamma function
Multivariate gamma function
In mathematics, the multivariate Gamma function, Γp, is a generalization of the Gamma function. It is useful in multivariate statistics, appearing in the probability density function of the Wishart and Inverse Wishart distributions....
defined as
In fact the above definition can be extended to any real n > p − 1. If n ≤ p − 2, then the Wishart no longer has a density—instead it represents a singular distribution.
Characteristic function
The characteristic functionCharacteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
of the Wishart distribution is
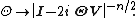
In other words,
where
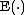denotes expectation. (Here 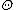and 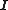are matrices the same size as 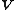( 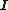is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
); and
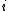is the square root of −1).Theorem
If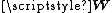 has a Wishart distribution with m degrees of freedom and variance matrix 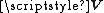—write 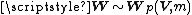—and 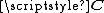is a q × p matrix of rank q, then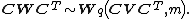Corollary 1
If is a nonzero constant vector, then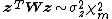.In this case,
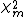isthe chi-squared distribution and
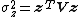(note that is a constant; it is positive because 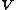is positive definite).Corollary 2
Consider the case where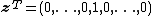 (that is, the jth element is one and all others zero). Then corollary 1 above shows thatgives the marginal distribution of each of the elements on the matrix's diagonal.
Noted statistician George Seber points out that the Wishart distribution is not called the “multivariate chi-squared distribution” because the marginal distribution of the off-diagonal elements is not chi-squared. Seber prefers to reserve the term multivariate
Multivariate statistics
Multivariate statistics is a form of statistics encompassing the simultaneous observation and analysis of more than one statistical variable. The application of multivariate statistics is multivariate analysis...
for the case when all univariate marginals belong to the same family.
Estimator of the multivariate normal distribution
The Wishart distribution is the sampling distributionSampling distribution
In statistics, a sampling distribution or finite-sample distribution is the probability distribution of a given statistic based on a random sample. Sampling distributions are important in statistics because they provide a major simplification on the route to statistical inference...
of the maximum-likelihood estimator
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
(MLE) of the covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
of a multivariate normal distribution with zero means. The derivation of the MLE is perhaps surprisingly subtle and elegant. It involves the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
and the reason why it can be better to view a scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
as the trace of a 1×1 matrix than as a mere scalar. See estimation of covariance matrices
Estimation of covariance matrices
In statistics, sometimes the covariance matrix of a multivariate random variable is not known but has to be estimated. Estimation of covariance matrices then deals with the question of how to approximate the actual covariance matrix on the basis of a sample from the multivariate distribution...
.
Bartlett decomposition
The Bartlett decomposition of a matrix W from a p-variate Wishart distribution with scale matrix V and n degrees of freedom is the factorization: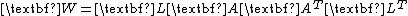where L is the Cholesky decomposition
Cholesky decomposition
In linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
of V, and:
where
and 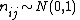independently.This provides a useful method for obtaining random samples from a Wishart distribution.
The possible range of the shape parameter
It can be shown that the Wishart distribution can be defined if and only if the shape parameter n belongs to the setThis set is named after Gindikin, who introduced it in the seventies
in the context of gamma distributions on homogeneous cones. However, for the new parameters in the discrete spectrum of the Gindikin ensemble, namely,
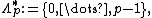
the corresponding Wishart distribution has no Lebesgue density.
Relationships to other distributions
- The Wishart distribution is related to the Inverse-Wishart distribution, denoted by
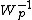, as follows: If 
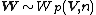and if we do the change of variables 
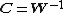, then 
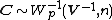. This relationship may be derived by noting that the absolute value of the Jacobian determinant of this change of variables is 
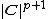, see for example equation (15.15) in. - The Wishart distribution is a conjugate priorConjugate priorIn Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
for the precision parameterPrecision (statistics)In statistics, the term precision can mean a quantity defined in a specific way. This is in addition to its more general meaning in the contexts of accuracy and precision and of precision and recall....
of the multivariate normal distribution, when the mean parameter is known.