Likelihood-ratio test
Encyclopedia
In statistics
, a likelihood ratio test is a statistical test used to compare the fit of two models, one of which (the null
model) is a special case of the other (the alternative model). The test is based on the likelihood
ratio, which expresses how many times more likely the data are under one model than the other. This likelihood ratio, or equivalently its logarithm
, can then be used to compute a p-value
, or compared to a critical value to decide whether to reject the null model in favour of the alternative model. When the logarithm of the likelihood ratio is used, the statistic is known as a log-likelihood ratio statistic, and the probability distribution
of this test statistic, assuming that the null model is true, can be approximated using Wilks' theorem.
In the case of distinguishing between two models, each of which has no unknown parameters, use of the likelihood ratio test can be justified by the Neyman–Pearson lemma, which demonstrates that such a test has the highest power
among all competitors.
recorded. The test statistic (usually denoted D) is twice the difference in these log-likelihoods:
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a likelihood ratio test is a statistical test used to compare the fit of two models, one of which (the null
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
model) is a special case of the other (the alternative model). The test is based on the likelihood
Likelihood
Likelihood is a measure of how likely an event is, and can be expressed in terms of, for example, probability or odds in favor.-Likelihood function:...
ratio, which expresses how many times more likely the data are under one model than the other. This likelihood ratio, or equivalently its logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
, can then be used to compute a p-value
P-value
In statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
, or compared to a critical value to decide whether to reject the null model in favour of the alternative model. When the logarithm of the likelihood ratio is used, the statistic is known as a log-likelihood ratio statistic, and the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of this test statistic, assuming that the null model is true, can be approximated using Wilks' theorem.
In the case of distinguishing between two models, each of which has no unknown parameters, use of the likelihood ratio test can be justified by the Neyman–Pearson lemma, which demonstrates that such a test has the highest power
Statistical power
The power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
among all competitors.
Use
Each of the two competing models, the null model and the alternative model, is separately fitted to the data and the log-likelihoodLikelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
recorded. The test statistic (usually denoted D) is twice the difference in these log-likelihoods:
-
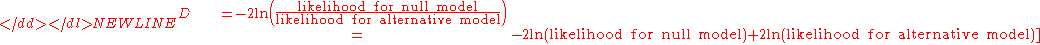
The model with more parameters will always fit at least as well (have a greater log-likelihood). Whether it fits significantly better and should thus be preferred is determined by deriving the probability or p-valueP-valueIn statistical significance testing, the p-value is the probability of obtaining a test statistic at least as extreme as the one that was actually observed, assuming that the null hypothesis is true. One often "rejects the null hypothesis" when the p-value is less than the significance level α ,...
of the difference D. In many cases, the probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the test statisticTest statisticIn statistical hypothesis testing, a hypothesis test is typically specified in terms of a test statistic, which is a function of the sample; it is considered as a numerical summary of a set of data that...
is approximately a chi-squared distribution with degrees of freedomDegrees of freedom (statistics)In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
equal to df2 − df1 , if the nested model with fewer parameters is correct. Symbols df1 and df2 represent the number of free parameters of models 1 and 2, the null model and the alternative model, respectively.
The test requires nested models, that is: models in which the more complex one can be transformed into the simpler model by imposing a set of constraints on the parameters.need examples or references to describe
For example: if model 1 has 1 free parameter and a log-likelihood of −8024 and the alternative model has 3 degrees of freedom and a LL of −8012, then the probability of this difference is that of chi-squared value of +2·(8024 − 8012) = 24 with 3 − 1 = 2 degrees of freedom. Certain assumptions must be met for the statistic to follow a chi-squared distribution and often empirical p-values are computed.
Background
The likelihood ratio, often denoted by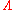 (the capital Greek letterGreek alphabetThe Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
(the capital Greek letterGreek alphabetThe Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
lambdaLambdaLambda is the 11th letter of the Greek alphabet. In the system of Greek numerals lambda has a value of 30. Lambda is related to the Phoenician letter Lamed . Letters in other alphabets that stemmed from lambda include the Roman L and the Cyrillic letter El...
), is the ratio of the likelihood functionLikelihood functionIn statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
varying the parameters over two different sets in the numerator and denominator.
A likelihood-ratio test is a statistical test for making a decision between two hypotheses based on the value of this ratio.
It is central to the NeymanJerzy NeymanJerzy Neyman , born Jerzy Spława-Neyman, was a Polish American mathematician and statistician who spent most of his professional career at the University of California, Berkeley.-Life and career:...
–PearsonEgon PearsonEgon Sharpe Pearson, CBE FRS was the only son of Karl Pearson, and like his father, a leading British statistician....
approach to statistical hypothesis testing, and, like statistical hypothesis testing generally, is both widely used and much criticized; see Criticism, below.
Simple-versus-simple hypotheses
A statistical model is often a parametrized family of probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s or probability mass functionProbability mass functionIn probability theory and statistics, a probability mass function is a function that gives the probability that a discrete random variable is exactly equal to some value...
s . A simple-vs-simple hypotheses test has completely specified models under both the nullNull hypothesisThe practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
. A simple-vs-simple hypotheses test has completely specified models under both the nullNull hypothesisThe practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
and alternative hypotheses, which for convenience are written in terms of fixed values of a notional parameter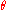 :
:

Note that under either hypothesis, the distribution of the data is fully specified; there are no unknown parameters to estimate. The likelihood ratio test statistic can be written as:
or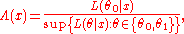
where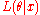 is the likelihood functionLikelihood functionIn statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
is the likelihood functionLikelihood functionIn statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
. Note that some references may use the reciprocal as the definition. In the form stated here, the likelihood ratio is small if the alternative model is better than the null model and the likelihood ratio test provides the decision rule as:
- If
 , do not reject
, do not reject 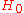 ;
;
- If
 , reject
, reject 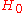 ;
; - Reject with probability
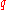 if
if 
The values are usually chosen to obtain a specified significance level
are usually chosen to obtain a specified significance level  , through the relation:
, through the relation:  . The Neyman-Pearson lemma states that this likelihood ratio test is the most powerfulStatistical powerThe power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
. The Neyman-Pearson lemma states that this likelihood ratio test is the most powerfulStatistical powerThe power of a statistical test is the probability that the test will reject the null hypothesis when the null hypothesis is actually false . The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis...
among all level- tests for this problem.
tests for this problem.
Definition (likelihood ratio test for composite hypotheses)
A null hypothesis is often stated by saying the parameter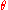 is in a specified subset
is in a specified subset  of the parameter space
of the parameter space  .
.
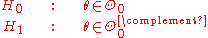
The likelihood functionLikelihood functionIn statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
is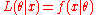 (with
(with  being the pdf or pmf) is a function of the parameter
being the pdf or pmf) is a function of the parameter 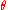 with
with  held fixed at the value that was actually observed, i.e., the data. The likelihood ratio test statistic is
held fixed at the value that was actually observed, i.e., the data. The likelihood ratio test statistic is
Here, the notation refers to the SupremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
notation refers to the SupremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
function.
A likelihood ratio test is any test with critical region (or rejection region) of the form where
where  is any number satisfying
is any number satisfying  . Many common test statistics such as the Z-testZ-testA Z-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution. Due to the central limit theorem, many test statistics are approximately normally distributed for large samples...
. Many common test statistics such as the Z-testZ-testA Z-test is any statistical test for which the distribution of the test statistic under the null hypothesis can be approximated by a normal distribution. Due to the central limit theorem, many test statistics are approximately normally distributed for large samples...
, the F-testF-testAn F-test is any statistical test in which the test statistic has an F-distribution under the null hypothesis.It is most often used when comparing statistical models that have been fit to a data set, in order to identify the model that best fits the population from which the data were sampled. ...
, Pearson's chi-squared testPearson's chi-squared testPearson's chi-squared test is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900...
and the G-testG-testIn statistics, G-tests are likelihood-ratio or maximum likelihood statistical significance tests that are increasingly being used in situations where chi-squared tests were previously recommended....
are tests for nested models and can be phrased as log-likelihood ratios or approximations thereof.
Interpretation
Being a function of the data , the LR is therefore a statisticStatisticA statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
, the LR is therefore a statisticStatisticA statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
. The likelihood-ratio test rejects the null hypothesis if the value of this statistic is too small. How small is too small depends on the significance level of the test, i.e., on what probability of Type I error is considered tolerable ("Type I" errors consist of the rejection of a null hypothesis that is true).
The numerator corresponds to the maximum likelihood of an observed outcome under the null hypothesisNull hypothesisThe practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
. The denominator corresponds to the maximum likelihood of an observed outcome varying parameters over the whole parameter space. The numerator of this ratio is less than the denominator. The likelihood ratio hence is between 0 and 1. Lower values of the likelihood ratio mean that the observed result was much less likely to occur under the null hypothesis as compared to the alternative. Higher values of the statistic mean that the observed outcome was more than or equally likely or nearly as likely to occur under the null hypothesis as compared to the alternative, and the null hypothesis cannot be rejected.
Distribution: Wilks' theorem
If the distribution of the likelihood ratio corresponding to a particular null and alternative hypothesis can be explicitly determined then it can directly be used to form decision regions (to accept/reject the null hypothesis). In most cases, however, the exact distribution of the likelihood ratio corresponding to specific hypotheses is very difficult to determine. A convenient result, attributed to Samuel S. WilksSamuel S. WilksSamuel Stanley Wilks was an American mathematician and academic who played an important role in the development of mathematical statistics, especially in regard to practical applications....
, says that as the sample size approaches
approaches  InfinityInfinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
InfinityInfinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...
, the test statistic for a nested model will be asymptotically
for a nested model will be asymptotically 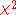 distributed with degrees of freedomDegrees of freedom (statistics)In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
distributed with degrees of freedomDegrees of freedom (statistics)In statistics, the number of degrees of freedom is the number of values in the final calculation of a statistic that are free to vary.Estimates of statistical parameters can be based upon different amounts of information or data. The number of independent pieces of information that go into the...
equal to the difference in dimensionality of and
and  . This means that for a great variety of hypotheses, a practitioner can compute the likelihood ratio
. This means that for a great variety of hypotheses, a practitioner can compute the likelihood ratio 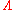 for the data and compare
for the data and compare  to the chi squared value corresponding to a desired statistical significanceStatistical significanceIn statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
to the chi squared value corresponding to a desired statistical significanceStatistical significanceIn statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
as an approximate statistical test.
Coin tossing
An example, in the case of Pearson's test, we might try to compare two coins to determine whether they have the same probability of coming up heads. Our observation can be put into a contingency table with rows corresponding to the coin and columns corresponding to heads or tails. The elements of the contingency table will be the number of times the coin for that row came up heads or tails. The contents of this table are our observation .
.
Heads
Tails
Coin 1
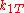
Coin 2
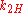
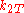
Here consists of the parameters
consists of the parameters 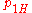 ,
, 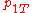 ,
, 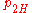 , and
, and 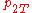 , which are the probability that coins 1 and 2 come up heads or tails. The hypothesis space
, which are the probability that coins 1 and 2 come up heads or tails. The hypothesis space  is defined by the usual constraints on a distribution,
is defined by the usual constraints on a distribution, 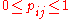 , and
, and 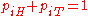 . The null hypothesis
. The null hypothesis 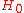 is the sub-space where
is the sub-space where 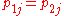 . In all of these constraints,
. In all of these constraints,  and
and  .
.
Writing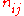 for the best values for
for the best values for 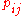 under the hypothesis
under the hypothesis  , maximum likelihood is achieved with
, maximum likelihood is achieved with
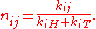
Writing for the best values for
for the best values for 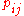 under the null hypothesis
under the null hypothesis  , maximum likelihood is achieved with
, maximum likelihood is achieved with
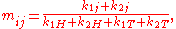
which does not depend on the coin .
.
The hypothesis and null hypothesis can be rewritten slightly so that they satisfy the constraints for the logarithm of the likelihood ratio to have the desired nice distribution. Since the constraint causes the two-dimensional to be reduced to the one-dimensional
to be reduced to the one-dimensional  , the asymptotic distribution for the test will be
, the asymptotic distribution for the test will be  , the
, the  distribution with one degree of freedom.
distribution with one degree of freedom.
For the general contingency table, we can write the log-likelihood ratio statistic as

Criticism
BayesianBayes' theoremIn probability theory and applications, Bayes' theorem relates the conditional probabilities P and P. It is commonly used in science and engineering. The theorem is named for Thomas Bayes ....
criticisms of classical likelihood ratio tests focus on two issues:- the supremumSupremumIn mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
function in the calculation of the likelihood ratio, saying that this takes no account of the uncertainty about θ and that using maximum likelihood estimates in this way can promote complicated alternative hypotheses with an excessive number of free parameters; - testing the probability that the sample would produce a result as extreme or more extreme under the null hypothesis, saying that this bases the test on the probability of extreme events that did not happen.
Instead they put forward methods such as Bayes factorBayes factorIn statistics, the use of Bayes factors is a Bayesian alternative to classical hypothesis testing. Bayesian model comparison is a method of model selection based on Bayes factors.-Definition:...
s, which explicitly take uncertainty about the parameters into account, and which are based on the evidence that did occur. From a frequentist approach, uncertainty about the parameters is taken into account in the probability distribution of the test statistic.
A frequentist reply to this critique is that likelihood ratio tests provide a practicable approach to statistical inference – they can easily be computed, by contrast to Bayesian posterior probabilities, which are more computationally intensive. The Bayesian reply to the latter is that computers obviate any such advantage.
A point in favour of using likelihood-ratio tests is that these satisfy the likelihood principleLikelihood principleIn statistics,the likelihood principle is a controversial principle of statistical inference which asserts that all of the information in a sample is contained in the likelihood function....
, which expresses the requirement put forward by many statisticians that statistical inferenceStatistical inferenceIn statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
should follow procedures based on the likelihood functionLikelihood functionIn statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
. Bayesian inference embodies the likelihood principle (ie that all the information from the sample data is expressed through the likelihood function), which using Bayes theorem it combines in a natural way with prior knowledge available prior to taking the sample data. In some fields, such as medical diagnosis and epidemiology, such information can be very important, reflecting for example the background prevalence of a condition or disease.
External links
- If