Statistical power
Encyclopedia
The power of a statistical test
is the probability that the test will reject the null hypothesis
when the null hypothesis is actually false (i.e. the probability of not committing a Type II error
, or making a false negative decision). The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis. As the power increases, the chances of a Type II error occurring decrease. The probability of a Type II error occurring is referred to as the false negative rate (β). Therefore power is equal to 1 − β, which is also known as the sensitivity
.
Power analysis can be used to calculate the minimum sample size
required so that one can be reasonably likely to detect an effect of a given size
. Power analysis can also be used to calculate the minimum effect size that is likely to be detected in a study using a given sample size. In addition, the concept of power is used to make comparisons between different statistical testing procedures: for example, between a parametric and a nonparametric test of the same hypothesis.
s to assess, or make inferences
about, a population
. In the concrete setting of a two-sample comparison, the goal is to assess whether the mean values of some attribute obtained for individuals in two sub-populations differ. For example, to test the null hypothesis that the mean
score
s of men and women on a test do not differ, samples of men and women are drawn, the test is administered to them, and the mean score of one group is compared to that of the other group using a statistical test such as the two-sample z-test. The power of the test is the probability that the test will find a statistically significant difference between men and women, as a function of the size of the true difference between those two populations. Note that power is the probability of finding a difference that does exist, as opposed to the likelihood of declaring a difference that does not exist (which is known as a Type I error, or "false positive").
A significance criterion is a statement of how unlikely a result must be, if the null hypothesis is true, to be considered significant. The most commonly used criteria are probabilities of 0.05 (5%, 1 in 20), 0.01 (1%, 1 in 100), and 0.001 (0.1%, 1 in 1000). If the criterion is 0.05, the probability of obtaining the observed effect when the null hypothesis is true must be less than 0.05, and so on. One easy way to increase the power of a test is to carry out a less conservative test by using a larger significance criterion. This increases the chance of rejecting the null hypothesis (i.e. obtaining a statistically significant result) when the null hypothesis is false, that is, reduces the risk of a Type II error. But it also increases the risk of obtaining a statistically significant result when the null hypothesis is true; that is, it increases the risk of a Type I error
.
The magnitude of the effect of interest in the population can be quantified in terms of an effect size
, where there is greater power to detect larger effects. An effect size can be a direct estimate of the quantity of interest, or it can be a standardized measure that also accounts for the variability in the population. For example, in an analysis comparing outcomes in a treated and control population, the difference of outcome means Y − X would be a direct measure of the effect size, whereas (Y − X)/σ where σ is the common standard deviation of the outcomes in the treated and control groups, would be a standardized effect size. If constructed appropriately, a standardized effect size, along with the sample size, will completely determine the power. An unstandardized (direct) effect size will rarely be sufficient to determine the power, as it does not contain information about the variability in the measurements.
The sample size determines the amount of sampling error inherent in a test result. Other things being equal, effects are harder to detect in smaller samples. Increasing sample size is often the easiest way to boost the statistical power of a test.
The precision with which the data are measured also influences statistical power. Consequently, power can often be improved by reducing the measurement error in the data. A related concept is to improve the "reliability" of the measure being assessed (as in psychometric reliability).
The design
of an experiment or observational study often influences the power. For example, in a two-sample testing situation with a given total sample size n, it is optimal to have equal numbers of observations from the two populations being compared (as long as the variances in the two populations are the same). In regression analysis and Analysis of Variance, there is an extensive theory, and practical strategies, for improving the power based on optimally setting the values of the independent variables in the model.
Power analysis is appropriate when the concern is with the correct rejection, or not, of a null hypothesis. In many contexts, the issue is less about determining if there is or is not a difference but rather with getting a more refined estimate
of the population effect size. For example, if we were expecting a population correlation
between intelligence and job performance of around .50, a sample size of 20 will give us approximately 80% power (alpha = .05, two-tail) to reject the null hypothesis of zero correlation. However, in doing this study we are probably more interested in knowing whether the correlation is .30 or .60 or .50. In this context we would need a much larger sample size in order to reduce the confidence interval of our estimate to a range that is acceptable for our purposes. Techniques similar to those employed in a traditional power analysis can be used to determine the sample size required for the width of a confidence interval to be less than a given value.
Many statistical analyses involve the estimation of several unknown quantities. In simple cases, all but one of these quantities is a nuisance parameter. In this setting, the only relevant power pertains to the single quantity that will undergo formal statistical inference. In some settings, particularly if the goals are more "exploratory," there may be a number of quantities of interest in the analysis. For example, in a multiple regression analysis
we may include several covariates of potential interest. In situations such as this where several hypotheses are under consideration, it is common that the powers associated with the different hypotheses differ. For instance, in multiple regression analysis, the power for detecting an effect of a given size is related to the variance of the covariate. Since different covariates will have different variances, their powers will differ as well.
Any statistical analysis involving multiple hypotheses
is subject to inflation of the type I error rate if appropriate measures are not taken. Such measures typically involve applying a higher threshold of stringency to reject a hypothesis in order to compensate for the multiple comparisons being made (e.g. as in the Bonferroni method). In this situation, the power analysis should reflect the multiple testing approach to be used. Thus, for example, a given study may be well powered to detect a certain effect size when only one test is to be made, but the same effect size may have much lower power if several tests are to be performed.
, hypothesis testing of the type used in classical power analysis is not done. In the Bayesian framework, one updates his or her prior beliefs using the data obtained in a given study. In principle, a study that would be deemed underpowered from the perspective of hypothesis testing could still be used in such an updating process. However, power remains a useful measure of how much a given experiment size can be expected to refine one's beliefs. A study with low power is unlikely to lead to a large change in beliefs.
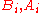denote the pre-treatment and post-treatment measures on subject i. The possible effect of the treatment should be visible in the differences 
, which we assume to be independently distributed, all with the same expected value and variance.
We proceed by analyzing D as in a one-sided t-test. The null hypothesis will be:
(no effect), and the alternative: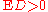 
(positive effect). The test statistic is:
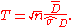
where n is the sample size,
is the average of the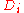 
and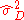 
is the sample variance. The null hypothesis is rejected when
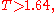
with 1.64 the approximate decision threshold for a level 0.05 test based on a normal approximation to the test statistic.
Now suppose that the alternative hypothesis is true and
. Then the power is
Since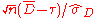
approximately follows a standard normal distribution when the alternative hypothesis is true, the approximate power can be calculated as
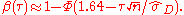
Note that according to this formula the power increases with the values of the parameter
. For a specific value of 
a higher power may be obtained by increasing the sample size n.
It is, of course, not possible to guarantee a sufficient large power for all values of
, as 
may be very close to 0. In fact the minimum (infimum
) value of the power is equal to the size of the test, in this example 0.05. However it is of no importance to distinguish between
and small positive values. If it is desirable to have enough power, say at least 0.90, to detect values of 
, the required sample size can be calculated approximately: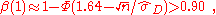
from which it follows that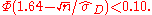
Hence
or
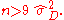
Further Explanations
Statistical hypothesis testing
A statistical hypothesis test is a method of making decisions using data, whether from a controlled experiment or an observational study . In statistics, a result is called statistically significant if it is unlikely to have occurred by chance alone, according to a pre-determined threshold...
is the probability that the test will reject the null hypothesis
Null hypothesis
The practice of science involves formulating and testing hypotheses, assertions that are capable of being proven false using a test of observed data. The null hypothesis typically corresponds to a general or default position...
when the null hypothesis is actually false (i.e. the probability of not committing a Type II error
Type I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
, or making a false negative decision). The power is in general a function of the possible distributions, often determined by a parameter, under the alternative hypothesis. As the power increases, the chances of a Type II error occurring decrease. The probability of a Type II error occurring is referred to as the false negative rate (β). Therefore power is equal to 1 − β, which is also known as the sensitivity
Sensitivity and specificity
Sensitivity and specificity are statistical measures of the performance of a binary classification test, also known in statistics as classification function. Sensitivity measures the proportion of actual positives which are correctly identified as such Sensitivity and specificity are statistical...
.
Power analysis can be used to calculate the minimum sample size
Sample size
Sample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
required so that one can be reasonably likely to detect an effect of a given size
Effect size
In statistics, an effect size is a measure of the strength of the relationship between two variables in a statistical population, or a sample-based estimate of that quantity...
. Power analysis can also be used to calculate the minimum effect size that is likely to be detected in a study using a given sample size. In addition, the concept of power is used to make comparisons between different statistical testing procedures: for example, between a parametric and a nonparametric test of the same hypothesis.
Background
Statistical tests use data from sampleSampling (statistics)
In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
s to assess, or make inferences
Statistical inference
In statistics, statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation...
about, a population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
. In the concrete setting of a two-sample comparison, the goal is to assess whether the mean values of some attribute obtained for individuals in two sub-populations differ. For example, to test the null hypothesis that the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
score
Score (statistics)
In statistics, the score, score function, efficient score or informant plays an important role in several aspects of inference...
s of men and women on a test do not differ, samples of men and women are drawn, the test is administered to them, and the mean score of one group is compared to that of the other group using a statistical test such as the two-sample z-test. The power of the test is the probability that the test will find a statistically significant difference between men and women, as a function of the size of the true difference between those two populations. Note that power is the probability of finding a difference that does exist, as opposed to the likelihood of declaring a difference that does not exist (which is known as a Type I error, or "false positive").
Factors influencing power
Statistical power may depend on a number of factors. Some of these factors may be particular to a specific testing situation, but at a minimum, power nearly always depends on the following three factors:- the statistical significanceStatistical significanceIn statistics, a result is called statistically significant if it is unlikely to have occurred by chance. The phrase test of significance was coined by Ronald Fisher....
criterion used in the test - the magnitude of the effect of interest in the population
- the sample sizeSample sizeSample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
used to detect the effect
A significance criterion is a statement of how unlikely a result must be, if the null hypothesis is true, to be considered significant. The most commonly used criteria are probabilities of 0.05 (5%, 1 in 20), 0.01 (1%, 1 in 100), and 0.001 (0.1%, 1 in 1000). If the criterion is 0.05, the probability of obtaining the observed effect when the null hypothesis is true must be less than 0.05, and so on. One easy way to increase the power of a test is to carry out a less conservative test by using a larger significance criterion. This increases the chance of rejecting the null hypothesis (i.e. obtaining a statistically significant result) when the null hypothesis is false, that is, reduces the risk of a Type II error. But it also increases the risk of obtaining a statistically significant result when the null hypothesis is true; that is, it increases the risk of a Type I error
Type I and type II errors
In statistical test theory the notion of statistical error is an integral part of hypothesis testing. The test requires an unambiguous statement of a null hypothesis, which usually corresponds to a default "state of nature", for example "this person is healthy", "this accused is not guilty" or...
.
The magnitude of the effect of interest in the population can be quantified in terms of an effect size
Effect size
In statistics, an effect size is a measure of the strength of the relationship between two variables in a statistical population, or a sample-based estimate of that quantity...
, where there is greater power to detect larger effects. An effect size can be a direct estimate of the quantity of interest, or it can be a standardized measure that also accounts for the variability in the population. For example, in an analysis comparing outcomes in a treated and control population, the difference of outcome means Y − X would be a direct measure of the effect size, whereas (Y − X)/σ where σ is the common standard deviation of the outcomes in the treated and control groups, would be a standardized effect size. If constructed appropriately, a standardized effect size, along with the sample size, will completely determine the power. An unstandardized (direct) effect size will rarely be sufficient to determine the power, as it does not contain information about the variability in the measurements.
The sample size determines the amount of sampling error inherent in a test result. Other things being equal, effects are harder to detect in smaller samples. Increasing sample size is often the easiest way to boost the statistical power of a test.
The precision with which the data are measured also influences statistical power. Consequently, power can often be improved by reducing the measurement error in the data. A related concept is to improve the "reliability" of the measure being assessed (as in psychometric reliability).
The design
Design of experiments
In general usage, design of experiments or experimental design is the design of any information-gathering exercises where variation is present, whether under the full control of the experimenter or not. However, in statistics, these terms are usually used for controlled experiments...
of an experiment or observational study often influences the power. For example, in a two-sample testing situation with a given total sample size n, it is optimal to have equal numbers of observations from the two populations being compared (as long as the variances in the two populations are the same). In regression analysis and Analysis of Variance, there is an extensive theory, and practical strategies, for improving the power based on optimally setting the values of the independent variables in the model.
Interpretation
Although there are no formal standards for power, most researchers assess the power of their tests using 0.80 as a standard for adequacy. This convention implies a four-to-one trade off between β-risk and α-risk. (β is the probability of a Type II error; α is the probability of a Type I error — 0.2 = 1 − 0.8 and 0.05 are conventional values for β and α). However, there will be times when this 4-to-1 weighting is inappropriate. In medicine, for example, tests are often designed in such a way that no false negatives (Type II errors) will be produced. But this inevitably raises the risk of obtaining a false positive (a Type I error). The rationale is that it is better to tell a healthy patient "we may have found something - let's test further," than to tell a diseased patient "all is well."Power analysis is appropriate when the concern is with the correct rejection, or not, of a null hypothesis. In many contexts, the issue is less about determining if there is or is not a difference but rather with getting a more refined estimate
Estimation theory
Estimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
of the population effect size. For example, if we were expecting a population correlation
Pearson product-moment correlation coefficient
In statistics, the Pearson product-moment correlation coefficient is a measure of the correlation between two variables X and Y, giving a value between +1 and −1 inclusive...
between intelligence and job performance of around .50, a sample size of 20 will give us approximately 80% power (alpha = .05, two-tail) to reject the null hypothesis of zero correlation. However, in doing this study we are probably more interested in knowing whether the correlation is .30 or .60 or .50. In this context we would need a much larger sample size in order to reduce the confidence interval of our estimate to a range that is acceptable for our purposes. Techniques similar to those employed in a traditional power analysis can be used to determine the sample size required for the width of a confidence interval to be less than a given value.
Many statistical analyses involve the estimation of several unknown quantities. In simple cases, all but one of these quantities is a nuisance parameter. In this setting, the only relevant power pertains to the single quantity that will undergo formal statistical inference. In some settings, particularly if the goals are more "exploratory," there may be a number of quantities of interest in the analysis. For example, in a multiple regression analysis
Regression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
we may include several covariates of potential interest. In situations such as this where several hypotheses are under consideration, it is common that the powers associated with the different hypotheses differ. For instance, in multiple regression analysis, the power for detecting an effect of a given size is related to the variance of the covariate. Since different covariates will have different variances, their powers will differ as well.
Any statistical analysis involving multiple hypotheses
Multiple comparisons
In statistics, the multiple comparisons or multiple testing problem occurs when one considers a set of statistical inferences simultaneously. Errors in inference, including confidence intervals that fail to include their corresponding population parameters or hypothesis tests that incorrectly...
is subject to inflation of the type I error rate if appropriate measures are not taken. Such measures typically involve applying a higher threshold of stringency to reject a hypothesis in order to compensate for the multiple comparisons being made (e.g. as in the Bonferroni method). In this situation, the power analysis should reflect the multiple testing approach to be used. Thus, for example, a given study may be well powered to detect a certain effect size when only one test is to be made, but the same effect size may have much lower power if several tests are to be performed.
A priori vs. post hoc analysis
Power analysis can either be done before (a priori or prospective power analysis) or after (post hoc or retrospective power analysis) data are collected. A priori power analysis is conducted prior to the research study, and is typically used in estimating sufficient sample sizes to achieve adequate power. Post-hoc power analysis is conducted after a study has been completed, and uses the obtained sample size and effect size to determine what the power was in the study, assuming the effect size in the sample is equal to the effect size in the population. Whereas the utility of prospective power analysis in experimental design is universally accepted, the usefulness of retrospective techniques is controversial. Falling for the temptation to use the statistical analysis of the collected data to estimate the power will result in uninformative and misleading values.Application
Funding agencies, ethics boards and research review panels frequently request that a researcher perform a power analysis, for example to determine the minimum number of animal test subjects needed for an experiment to be informative. In frequentist statistics, an underpowered study is unlikely to allow one to choose between hypotheses at the desired significance level. In Bayesian statisticsBayesian statistics
Bayesian statistics is that subset of the entire field of statistics in which the evidence about the true state of the world is expressed in terms of degrees of belief or, more specifically, Bayesian probabilities...
, hypothesis testing of the type used in classical power analysis is not done. In the Bayesian framework, one updates his or her prior beliefs using the data obtained in a given study. In principle, a study that would be deemed underpowered from the perspective of hypothesis testing could still be used in such an updating process. However, power remains a useful measure of how much a given experiment size can be expected to refine one's beliefs. A study with low power is unlikely to lead to a large change in beliefs.
Example
We study the effect of a treatment on some quantity, and compare research subjects by measuring the quantity before and after the treatment, analyzing the data using a paired t-test. Let denote the pre-treatment and post-treatment measures on subject i. The possible effect of the treatment should be visible in the differences , which we assume to be independently distributed, all with the same expected value and variance.We proceed by analyzing D as in a one-sided t-test. The null hypothesis will be:
(no effect), and the alternative: 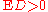(positive effect). The test statistic is: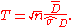where n is the sample size,
is the average of the 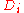and 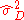is the sample variance. The null hypothesis is rejected when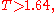with 1.64 the approximate decision threshold for a level 0.05 test based on a normal approximation to the test statistic.
Now suppose that the alternative hypothesis is true and
. Then the power isSince
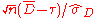approximately follows a standard normal distribution when the alternative hypothesis is true, the approximate power can be calculated as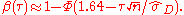Note that according to this formula the power increases with the values of the parameter
. For a specific value of a higher power may be obtained by increasing the sample size n.It is, of course, not possible to guarantee a sufficient large power for all values of
, as may be very close to 0. In fact the minimum (infimumInfimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
) value of the power is equal to the size of the test, in this example 0.05. However it is of no importance to distinguish between
and small positive values. If it is desirable to have enough power, say at least 0.90, to detect values of , the required sample size can be calculated approximately: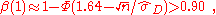from which it follows that
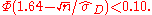
Hence
or
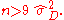
See also
- Effect sizeEffect sizeIn statistics, an effect size is a measure of the strength of the relationship between two variables in a statistical population, or a sample-based estimate of that quantity...
- Sample sizeSample sizeSample size determination is the act of choosing the number of observations to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample...
- Neyman–Pearson lemma
- Uniformly most powerful testUniformly most powerful testIn statistical hypothesis testing, a uniformly most powerful test is a hypothesis test which has the greatest power 1 − β among all possible tests of a given size α...
External links
- Hypothesis Testing and Statistical Power of a Test
- G*Power – A free program for Statistical Power Analysis for Mac OS and MS-DOS
- Effect Size Calculators Calculate d and r from a variety of statistics.
- R/Splus package of power analysis functions along the lines of Cohen (1988)
- Examples of all ANOVA and ANCOVA models with up to three treatment factors, including tools to estimate design power
- Free A-priori Sample Size Calculator for Multiple Regression from Daniel Soper's Free Statistics Calculators website. Computes the minimum required sample size for a study, given the alpha level, the number of predictors, the anticipated effect size, and the desired statistical power level.
- Power calculator from Russ Lenth, University of Iowa
Further Explanations